Ий этап: построение минимальных ДНФ.
Минимальные ДНФ функции являются тупиковыми ДНФ. Поэтому, после того как все тупиковые ДНФ построены, нужно отобрать те из них, которые имеют наименьшую сложность (таких может быть несколько). Это и будут минимальные ДНФ.
Например, для функции  обе тупиковые ДНФ имеют сложность, равную шести, и, следовательно, обе являются минимальными.
обе тупиковые ДНФ имеют сложность, равную шести, и, следовательно, обе являются минимальными.
Упражнение 22. Построить минимальные ДНФ функции:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
◄ а) 1 этап. Строим сокращенную ДНФ функции:




 .
.
2-ой и 3-й этапы для данной функции не актуальны. Действительно, функция  зависит от переменных
зависит от переменных  существенным образом и, значит, не может быть представлена ДНФ, содержащей менее трех букв. Следовательно, сокращенная ДНФ
существенным образом и, значит, не может быть представлена ДНФ, содержащей менее трех букв. Следовательно, сокращенная ДНФ  функции
функции  является также тупиковой и минимальной.
является также тупиковой и минимальной.
 |  | 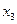 |  |  |
б)1-й этап. Строим сокращенную ДНФ функции:





 .
.
Переход I: операция неполного склеивания применена к парам конъюнкций 1 и 2, 1 и 4, 2 и 5, 3 и 7, 4 и 5, 5 и 6, 6 и 7.
Переход II: применена операция поглощения - каждая из конъюнкций 4-го ранга поглощена какой-то из конъюнкций 3-го ранга.
Переход III: операция неполного склеивания применена к парам конъюнкций 8 и 12, 9 и 10.
Переход IV: применена операция поглощения и убраны дублирующие члены.
Итак, мы нашли сокращенную ДНФ функции:  .
.
2-й этап. Введем обозначения для простых импликант функции:  ,
,  ,
,  ,
,  . Составим импликантную таблицу:
. Составим импликантную таблицу:
 | |||||||
 | |||||||
 | |||||||
 |
Тогда

 .
.
Таким образом, имеем две тупиковых ДНФ, реализующие функцию  :
:  и
и  .
.
3-й этап. Тупиковые ДНФ функции  имеют одинаковую сложность (равную восьми), и, следовательно, обе являются минимальными.
имеют одинаковую сложность (равную восьми), и, следовательно, обе являются минимальными.
в), г) решите самостоятельно. ►
§ 2.4. Классы Поста и полнота
2.4.1. Понятие о полноте системы булевых функций
Определение. Множество булевых функций  называется полной системой, если любая булева функция из
называется полной системой, если любая булева функция из 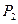 может быть реализована формулой над
может быть реализована формулой над  .
.
Упражнение 2.25. Доказать, что  - полная система.
- полная система.
◄ Возможны два случая:
1.  . Тогда
. Тогда  и может быть реализована в виде СКНФ.
и может быть реализована в виде СКНФ.
2.  . Тогда
. Тогда  может быть реализована в виде СДНФ.
может быть реализована в виде СДНФ.
Таким образом, любая булева функция может быть реализована формулой над множеством  , что и означает полноту этой системы функций. ►
, что и означает полноту этой системы функций. ►
Теорема (о полноте двух систем). Пусть заданы две системы функций из 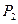 :
:  и
и  . Тогда, если система
. Тогда, если система  - полная и каждая ее функция может быть реализована формулой над
- полная и каждая ее функция может быть реализована формулой над  , то система
, то система  тоже полная.
тоже полная.
Докажем это утверждение. Пусть  - произвольная функция из
- произвольная функция из 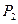 . Надо показать, что ее можно реализовать формулой над
. Надо показать, что ее можно реализовать формулой над  . Рассуждаем так. В силу полноты
. Рассуждаем так. В силу полноты 
 реализуется формулой над
реализуется формулой над  , т.е.
, т.е.  . В свою очередь, по условию
. В свою очередь, по условию  реализуются формулами над
реализуются формулами над  , т.е.
, т.е.  . Следовательно, в формуле
. Следовательно, в формуле  мы можем исключить вхождение символов функций
мы можем исключить вхождение символов функций  , заменив их соответствующими формулами:
, заменив их соответствующими формулами:  . Полученное выражение определяет формулу над
. Полученное выражение определяет формулу над  , реализующую
, реализующую  .
.
Упражнение 2.26. Используя теорему о полноте двух систем, доказать полноту системы булевых функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
◄ а)Докажем, что  - полная система. Действительно, пусть
- полная система. Действительно, пусть  и
и  . Система
. Система  - полная и, поскольку
- полная и, поскольку  , то каждая функция этой системы выражается формулой над
, то каждая функция этой системы выражается формулой над  . Таким образом, условия теоремы о полноте двух систем выполнены и, значит, система
. Таким образом, условия теоремы о полноте двух систем выполнены и, значит, система  - полная система.
- полная система.
б) Докажем, что  полная система. Действительно, пусть
полная система. Действительно, пусть  и
и  . Имеем:
. Имеем:  или
или  . Следовательно,
. Следовательно,  и
и  . Таким образом, каждая функция полной системы
. Таким образом, каждая функция полной системы  реализуется формулой над
реализуется формулой над  . Следовательно, условия теоремы о полноте двух систем выполнены и, значит,
. Следовательно, условия теоремы о полноте двух систем выполнены и, значит,  - полная система.
- полная система.
в) и г)докажите самостоятельно. ►
2.4.2. Реализация булевых функций полиномом Жегалкина
Возьмем произвольную функцию  . Поставим цель – реализовать ее в виде суммы (по модулю два) слагаемых, каждое из которых представляет собой конъюнкцию нескольких переменных.
. Поставим цель – реализовать ее в виде суммы (по модулю два) слагаемых, каждое из которых представляет собой конъюнкцию нескольких переменных.
Вначале рассмотрим эту задачу на конкретном примере. Для функции  имеем:
имеем:

 .
.
В ходе преобразований мы воспользовались несколькими доказанными ранее (упр. 2.12) равносильностями: 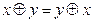 ,
, 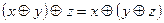 ,
, 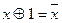 ,
, 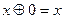 ,
, 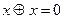 ,
, 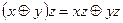 .
.
Аналогичным образом можно поступать с произвольной функцией: сначала реализовать ее в виде СДНФ или СКНФ; затем, воспользовавшись законом де Моргана, избавиться от дизъюнкции; раскрыть скобки, воспользовавшись дистрибутивностью операций сложения по модулю два и конъюнкции; после этого полученное выражение упростить, используя тождества  ,
,  ,
,  ,
,  ,
,  . В результате функция окажется реализована формулой, представляющей собой сумму (по модулю два) конъюнкций переменных. Формулы такого вида называют полиномами Жегалкина.
. В результате функция окажется реализована формулой, представляющей собой сумму (по модулю два) конъюнкций переменных. Формулы такого вида называют полиномами Жегалкина.
Дадим строгое определение полинома Жегалкина. Пусть M – произвольное подмножество булевого куба  ,
,  ,
,  - номер вектора
- номер вектора  ,
,  - его вес,
- его вес,  - номера отличных от нуля координат вектора
- номера отличных от нуля координат вектора  .
.
Определение. Формула вида
 , (***)
, (***)
где суммирование ведется по модулю два, а коэффициенты  равны либо 0, либо 1, называется полиномом Жегалкина от
равны либо 0, либо 1, называется полиномом Жегалкина от  переменных.
переменных.
Если суммирование в формуле (***), ведется по всем булевым векторам длины n, слагаемые идут в порядке возрастания номеров булевых векторов и  , то говорят, что полином Жегалкина записан в канонической форме.
, то говорят, что полином Жегалкина записан в канонической форме.
Наибольший из рангов элементарных конъюнкций, входящих в полином с единичными коэффициентами, называется степенью полинома.
Возможно, строгое определение канонического полинома Жегалкина показалось Вам неясным. Лучший способ его осознать – переформировать применительно к какому-нибудь частному случаю, например, случаю 2-х переменных.
Рассуждаем так. Согласно определению в формуле (***) слагаемых столько, сколько булевых векторов в множестве  , т.е. 4; слагаемые идут в порядке возрастания номеров булевых векторов, т.е. первое слагаемое соответствует булевому вектору (0,0), второе - (0,1), третье - (1,0), четвертое - (1,1). Слагаемые представляют собой конъюнкции, в которые входят только те переменные, значения которых в соответствующем булевом векторе равны 1, конъюнкции помножены на числовой коэффициент. Таким образом, слагаемое, соответствующее булевому вектору (0,0) (его номер 0), имеет вид
, т.е. 4; слагаемые идут в порядке возрастания номеров булевых векторов, т.е. первое слагаемое соответствует булевому вектору (0,0), второе - (0,1), третье - (1,0), четвертое - (1,1). Слагаемые представляют собой конъюнкции, в которые входят только те переменные, значения которых в соответствующем булевом векторе равны 1, конъюнкции помножены на числовой коэффициент. Таким образом, слагаемое, соответствующее булевому вектору (0,0) (его номер 0), имеет вид  ; слагаемое, соответствующее булевому вектору (0,1) (его номер 1), имеет вид
; слагаемое, соответствующее булевому вектору (0,1) (его номер 1), имеет вид  ; слагаемое, соответствующее булевому вектору (1,0) (его номер 2), имеет вид
; слагаемое, соответствующее булевому вектору (1,0) (его номер 2), имеет вид  ; слагаемое, соответствующее булевому вектору (1,1) (его номер 3), имеет вид
; слагаемое, соответствующее булевому вектору (1,1) (его номер 3), имеет вид  . Итак, канонический полином Жегалкина от 2-х переменных - это формула вида
. Итак, канонический полином Жегалкина от 2-х переменных - это формула вида  .
.
Рассуждая аналогично, выпишем в общем виде канонический полином Жегалкина от 3-х переменных -  (Это удобно делать, имея перед глазами таблицу истинности функции трех переменных, поскольку в этой таблице булевы вектора перечисляются в нужном нам порядке).
(Это удобно делать, имея перед глазами таблицу истинности функции трех переменных, поскольку в этой таблице булевы вектора перечисляются в нужном нам порядке).
Упражнение 2.27. Найти число канонических полиномов Жегалкина от  переменных.
переменных.
◄ Каждый канонический полином Жегалкина от  переменных однозначно определяется набором своих коэффициентов
переменных однозначно определяется набором своих коэффициентов  . Каждый такой набор можно рассматривать как булев вектор длины
. Каждый такой набор можно рассматривать как булев вектор длины  . Следовательно, канонических полиномов Жегалкина от
. Следовательно, канонических полиномов Жегалкина от  переменных столько же, сколько булевых векторов длины
переменных столько же, сколько булевых векторов длины  , т.е.
, т.е.  . ►
. ►
Заметим, что каждый полином Жегалкина от n переменных можно записать в канонической форме. Например, полином Жегалкина от двух переменных  в канонической форме запишется так:
в канонической форме запишется так:  .
.
Выше на примере функции  мы показали, как можно реализовать функцию в виде полинома Жегалкина. Полученный полином можно переписать в канонической форме
мы показали, как можно реализовать функцию в виде полинома Жегалкина. Полученный полином можно переписать в канонической форме  . В связи с этим естественно задаться вопросом: каждую ли булеву функцию можно реализовать в виде канонического полинома Жегалкина? Оказывается, да. Действительно, с произвольной функцией можно действовать так же как с функцией
. В связи с этим естественно задаться вопросом: каждую ли булеву функцию можно реализовать в виде канонического полинома Жегалкина? Оказывается, да. Действительно, с произвольной функцией можно действовать так же как с функцией  : сначала реализовать ее в виде СДНФ или СКНФ; затем, воспользовавшись законом де Моргана, избавиться от дизъюнкции; раскрыть скобки, воспользовавшись дистрибутивностью операций сложения по модулю два и конъюнкции; после этого полученное выражение упростить, используя тождества
: сначала реализовать ее в виде СДНФ или СКНФ; затем, воспользовавшись законом де Моргана, избавиться от дизъюнкции; раскрыть скобки, воспользовавшись дистрибутивностью операций сложения по модулю два и конъюнкции; после этого полученное выражение упростить, используя тождества  ,
,  ,
,  ,
,  ,
,  . В результате функция окажется реализованной в виде полинома Жегалкина, который легко переписать в канонической форме.
. В результате функция окажется реализованной в виде полинома Жегалкина, который легко переписать в канонической форме.
Положим, мы построили для функции канонический полином Жегалкина. Естественно поинтересоваться: нельзя ли, действуя иначе, получить для той же функции другой канонический полином Жегалкина. Оказывается, нельзя.
Действительно, число канонических полиномов Жегалкина от  переменных равно
переменных равно  и число функций от
и число функций от  переменных равно
переменных равно  . Предположим, что найдется функция, представление которой в виде канонического полинома Жегалкина не единственно. Поскольку число булевых функций
. Предположим, что найдется функция, представление которой в виде канонического полинома Жегалкина не единственно. Поскольку число булевых функций  переменных и число канонических полиномов Жегалкина от
переменных и число канонических полиномов Жегалкина от  переменных одинаково, то из неоднозначности представления следует, что найдется канонический полином Жегалкина, реализующий не менее двух функций, что невозможно. Пришли к противоречию, следовательно, наше предположение о неоднозначности представления было неверным.
переменных одинаково, то из неоднозначности представления следует, что найдется канонический полином Жегалкина, реализующий не менее двух функций, что невозможно. Пришли к противоречию, следовательно, наше предположение о неоднозначности представления было неверным.
Мы доказали теорему: каждая булева функция от  переменных может быть реализована в виде канонического полинома Жегалкина от
переменных может быть реализована в виде канонического полинома Жегалкина от  переменных, причем единственным образом.
переменных, причем единственным образом.
Для нахождения полинома Жегалкина, реализующего функцию  , применяют два способа: метод равносильных преобразований и метод неопределенных коэффициентов.
, применяют два способа: метод равносильных преобразований и метод неопределенных коэффициентов.
Методом равносильных преобразований мы уже пользовались, когда искали полином Жегалкина функции  .
.
Упражнение 2.28. Используя метод равносильных преобразований, найти полином Жегалкина, реализующий функцию:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
◄ а)  .
.
б)  .
.
в) и г)решите самостоятельно. ►
Метод неопределенных коэффициентов состоит в следующем. Пусть функция  зависит от
зависит от  переменных. В общем виде записывают канонический полином Жегалкина
переменных. В общем виде записывают канонический полином Жегалкина  от
от  переменных. Для каждого набора
переменных. Для каждого набора  значений переменных составляют уравнение
значений переменных составляют уравнение  . В результате получают систему из
. В результате получают систему из  уравнений, которая однозначно определяет коэффициенты полинома.
уравнений, которая однозначно определяет коэффициенты полинома.
Упражнение 2.29. Используя метод неопределенных коэффициентов, найти полином Жегалкина, реализующий функцию:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
◄ а)Зададим функцию  таблично:
таблично:
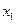 | 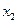 |  |
Канонический полином Жегалкина от двух переменных имеет вид:  . Поэтому должны выполняться равенства:
. Поэтому должны выполняться равенства:
 ;
;
 ;
;
 ;
;
 .
.
Откуда последовательно находим  ,
,  ,
,  ,
,  . Таким образом,
. Таким образом,  .
.
б)
 |  | 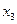 |  |
Запишем в общем виде канонический полином Жегалкина от трех переменных:
 .
.
Нам нужно подобрать такие коэффициенты  , чтобы на каждом наборе значений переменных выполнялось равенство:
, чтобы на каждом наборе значений переменных выполнялось равенство:  :
:
 ;
;  ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Коэффициенты найдены и можно записать канонический полином Жегалкина:  .
.
Каноническая форма полинома Жегалкина довольно громоздкая и в практическом плане не имеет каких-либо преимуществ перед любой другой формой. Поэтому имеет смысл упростить полученное выражение, опустив нулевые члены и единичные сомножители:  .
.
в) и г)решите самостоятельно. ►
2.4.3 Классы Поста
Определение. Говорят, что булева функция сохраняет 0, если  .
.
Обозначим через  множество функций от
множество функций от  переменных, сохраняющих 0, а через
переменных, сохраняющих 0, а через  – множество всех булевых функций, сохраняющих 0, т.е.
– множество всех булевых функций, сохраняющих 0, т.е.  .
.
Например,  , т.к.
, т.к.  ;
;  , т.к.
, т.к.  .
.
Определение. Говорят, что булева функция сохраняет 1, если  .
.
Обозначим через  множество функций от
множество функций от  переменных, сохраняющих 1, а через
переменных, сохраняющих 1, а через  – множество всех булевых функций, сохраняющих 1, т.е.
– множество всех булевых функций, сохраняющих 1, т.е.  .
.
Например,  , т.к.
, т.к.  ;
;
 , т.к.
, т.к.  .
.
Упражнение 2.30. а)Какие из функцийодной переменной принадлежат, а какие не принадлежат множествам  ,
,  ?
?
б) Какие из элементарных функций двух переменных принадлежат, а какие не принадлежат множествам  ,
,  ?
?
◄ а)  ,
,  ,
,  ,
,  .
.
б) решить самостоятельно.►
Упражнение 2.31. а) Перечислите векторы значений булевых функций 2-х переменных, сохраняющих 0.
б) Перечислите векторы значений булевых функций 2-х переменных, сохраняющих как 0, так и 1.
в) Сколько имеется булевых функций от  переменных, сохраняющих 0?
переменных, сохраняющих 0?
г) Сколько имеется булевых функций от  переменных, сохраняющих 1?
переменных, сохраняющих 1?
д) Сколько булевых функций содержится во множестве  ?
?
е) Сколько булевых функций содержится во множестве  ?
?
◄ а)иб) решите самостоятельно.
в)Пусть  . Вектор значений такой функции имеет
. Вектор значений такой функции имеет  координат, первая из которых равна 0, т.е.
координат, первая из которых равна 0, т.е.  . Следовательно, функций от
. Следовательно, функций от  переменных, сохраняющих 0, столько же, сколько булевых векторов длины
переменных, сохраняющих 0, столько же, сколько булевых векторов длины  , т.е.
, т.е.  .
.
г) и д) решите самостоятельно.
е) Разобьем множество  на три подмножества: в первое включим функции, сохраняющие 0, но не сохраняющие 1, во второе – функции, сохраняющие 1, но не сохраняющие 0, в третье – функции, сохраняющие как 0, так и 1. В первом подмножестве содержится
на три подмножества: в первое включим функции, сохраняющие 0, но не сохраняющие 1, во второе – функции, сохраняющие 1, но не сохраняющие 0, в третье – функции, сохраняющие как 0, так и 1. В первом подмножестве содержится  функций (первая и последняя координаты вектора значений этих функция равны 0), во втором -
функций (первая и последняя координаты вектора значений этих функция равны 0), во втором -  (первая и последняя координаты вектора значений этих функция равны 1), в третьем -
(первая и последняя координаты вектора значений этих функция равны 1), в третьем -  (первая координата вектора значений этих функция равна 0, последняя - 1). Следовательно,
(первая координата вектора значений этих функция равна 0, последняя - 1). Следовательно,  .
.
Другой подход к решению – использование формулы мощности объединения множеств:
 ►
►
Определение. Булева функция называется самодвойственной, если  , т.е. на любом наборе
, т.е. на любом наборе  значений переменных
значений переменных  выполняется равенство т.е.
выполняется равенство т.е.  .
.
Иначе говоря, булева функция самодвойственная, если на противоположных наборах она принимает противоположные значения
Обозначим через  множество самодвойственных функций от
множество самодвойственных функций от  переменных, а через
переменных, а через  – множество всех самодвойственных функций; т.е.
– множество всех самодвойственных функций; т.е.  .
.
Упражнение 2.32.Дать определение несамодвойственной функции.
◄Булева функция несамодвойственная, если существует такой набор  значений переменных
значений переменных  такой, что
такой, что  .►
.►
Например,  , т.к.
, т.к.  .
.
Упражнение 2.33. а)Перечислите самодвойственные функцииодной переменной.
б) Перечислите элементарные самодвойственные функции двух переменных.
◄ а)  ,
,  ,
,  ,
,  , таким образом, среди функций одного аргумента самодвойственными являются тождественная функция и отрицание.
, таким образом, среди функций одного аргумента самодвойственными являются тождественная функция и отрицание.
б) решить самостоятельно.►
Определение. Если для любого 
 (
(  ), то говорят, что вектор
), то говорят, что вектор  предшествует вектору
предшествует вектору  и пишут
и пишут  .
.
Обратите внимание, если номер вектора  меньше номера вектора
меньше номера вектора  (и, значит, в таблице истинности
(и, значит, в таблице истинности  стоит выше
стоит выше  ), то это еще не значит, что
), то это еще не значит, что  предшествует
предшествует  . Чтобы выяснить предшествует ли один вектор другому, нужно сравнить их координаты (первую с первой, вторую со второй, и т.д.). Например, вектор
. Чтобы выяснить предшествует ли один вектор другому, нужно сравнить их координаты (первую с первой, вторую со второй, и т.д.). Например, вектор  предшествует
предшествует  , но не предшествует вектору
, но не предшествует вектору  . Еще примеры:
. Еще примеры:  ;
;  . Заметьте, есть пары векторов, в которых ни один из векторов не предшествует другому.
. Заметьте, есть пары векторов, в которых ни один из векторов не предшествует другому.
Если имеет место хотя бы одно из соотношений  или
или  , то
, то  и
и  называют сравнимыми. В противном случае – несравнимыми.
называют сравнимыми. В противном случае – несравнимыми.
Упражнение 2.32. а) Перечислите булевы вектора, предшествующие  .
.
б)Перечислите булевы вектора, предшествующие  .
.
◄ а)Булев вектор будет предшествовать вектору  , если его первая и третья координаты будут либо равны 0, либо 1, а вторая и четвертая равны 0. Этим условиям удовлетворяют вектора
, если его первая и третья координаты будут либо равны 0, либо 1, а вторая и четвертая равны 0. Этим условиям удовлетворяют вектора  ,
,  ,
,  , а также сам вектор
, а также сам вектор  .
.
б) решить самостоятельно.►
Упражнение 2.35. а)Сколько существует булевых векторов, предшествующих вектору  ?
?
б)Сколько существует булевых векторов, которым предшествует вектор (101000101)?
◄ а) Вектора, предшествующие вектору  , имеют вид
, имеют вид  , где
, где  выбираются из множества
выбираются из множества  . Для подсчета используем правило произведения. Вначале выбираем значение
. Для подсчета используем правило произведения. Вначале выбираем значение  (это можно сделать двумя способами – взять 0 или 1), затем выбираем значение
(это можно сделать двумя способами – взять 0 или 1), затем выбираем значение  (0 или 1), и последним выбираем значение
(0 или 1), и последним выбираем значение  (0 или 1). Следовательно, общее число предшествующих векторов равно
(0 или 1). Следовательно, общее число предшествующих векторов равно  .
.
б) Решить самостоятельно.►
Определение. Говорят, что булева функция  монотонна, если для любых наборов
монотонна, если для любых наборов  и
и  значений переменных, таких что
значений переменных, таких что  , выполняется неравенство
, выполняется неравенство  .
.
Обозначим через  множество монотонных функций от
множество монотонных функций от  переменных, а через
переменных, а через  – множество всех монотонных функций; т.е.
– множество всех монотонных функций; т.е.  .
.
Упражнение 2.36.Дать определение немонотонной функции.
◄Булева функция  немонотонная, если найдутся такие наборы
немонотонная, если найдутся такие наборы  и
и  значений переменных, что
значений переменных, что  , а
, а  . ►
. ►
В случае функции одной переменной функция монотонна при выполнении неравенства  . В частном случае двух переменных функция
. В частном случае двух переменных функция  монотонна, если выполняются неравенства:
монотонна, если выполняются неравенства:  ,
,  ,
,  ,
,  ,
,  . Обратите внимание: так как в паре векторов
. Обратите внимание: так как в паре векторов  ни один не предшествует другому, то и значения
ни один не предшествует другому, то и значения  и
и  не сравниваются. Например, функции
не сравниваются. Например, функции  - монотонны, а функции
- монотонны, а функции  немонотонны.
немонотонны.
Упражнение 2.37. Выяснить, монотонна или нет функция:
а)  ; б)
; б)  .
.
 |  | 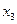 |  |  |
◄ а)Будем последовательно перебирать пары булевых векторов, отбирать из них сравнимые и сопоставлять значения функции  на векторах этих пар.
на векторах этих пар.
Перебор можно вести, придерживаясь такой схемы: сначала перебираем пары с вектором  ,
,
затем пары с вектором  (вектор
(вектор  уже не рассматриваем), затем пары с вектором
уже не рассматриваем), затем пары с вектором  (вектора
(вектора  и
и  уже не рассматриваем) и т.д.
уже не рассматриваем) и т.д.
Вектор  предшествует всем прочим булевым векторам длины 3, при этом значение функции на этом векторе, будучи равным нулю, меньше либо равно значениям функции на всех других векторах. Этот факт не позволяет сделать никаких выводов относительно монотонности функции
предшествует всем прочим булевым векторам длины 3, при этом значение функции на этом векторе, будучи равным нулю, меньше либо равно значениям функции на всех других векторах. Этот факт не позволяет сделать никаких выводов относительно монотонности функции  , поэтому переходим к рассмотрению пар с вектором
, поэтому переходим к рассмотрению пар с вектором  . Вектор
. Вектор  предшествует векторам
предшествует векторам  ,
,  ,
,  , при этом
, при этом  , однако уже
, однако уже  . Следовательно, условие монотонности нарушено, и, значит, функция немонотонна.
. Следовательно, условие монотонности нарушено, и, значит, функция немонотонна.
б) Последовательно перебрав все пары сравнимых векторов, убеждаемся, что функция монотонна.►
Обратите внимание: для вывода о не монотонности функции достаточно указать два булевых вектора  и
и  , такие что
, такие что  , а
, а  . Для вывода о монотонности, нужно сравнить значения функции на всех парах сравнимых векторов.
. Для вывода о монотонности, нужно сравнить значения функции на всех парах сравнимых векторов.
Определение. Говорят, что булева функция линейна, если степень ее канонического полинома Жегалкина меньше либо равна 1.
Иначе говоря, функция линейна, если ее полином Жегалкина имеет вид  .
.
Обозначим через  множество линейных функций от
множество линейных функций от  переменных, а через
переменных, а через  – множество всех линейных булевых функций, т.е.
– множество всех линейных булевых функций, т.е.  .
.
Упражнение 2.38.Дать определение нелинейной функции.
◄Булева функция  нелинейна, если степень ее канонического полинома Жегалкина больше либо равна двум. ►
нелинейна, если степень ее канонического полинома Жегалкина больше либо равна двум. ►
Из определений следует: для того, чтобы определить, является функция линейной или нет, необходимо вначале реализовать ее полиномом Жегалкина.
Например, все функции одной переменной  линейны;
линейны; 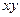 ,
,  ,
,  ,
,  линейными не являются.
линейными не являются.
Упражнение 2.39. а) Выписать полиномы Жегалкина линейных булевых функций от 2-х переменных.
б) Выяснить, сколько имеется линейных булевых функций от  переменных.
переменных.
◄ а) решите самостоятельно.
б) Между булевыми функциями  переменных и каноническими полиномами Жегалкина от
переменных и каноническими полиномами Жегалкина от  переменных существует взаимно однозначное соответствие, значит, линейных булевых функций от
переменных существует взаимно однозначное соответствие, значит, линейных булевых функций от  переменных столько же, сколько канонических полиномов Жегалкина вида
переменных столько же, сколько канонических полиномов Жегалкина вида  . Каждый такой полином Жегалкина определяется набором коэффициентов
. Каждый такой полином Жегалкина определяется набором коэффициентов  , а количество таких наборов равно
, а количество таких наборов равно  . Значит,
. Значит,  .►
.►
Упражнение 2.40. Определите, каким из классов Поста принадлежат функции:
а)  ; б)
; б)  ; а)
; а) 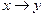 ; б)
; б)  .
.
◄ а)  . Имеем:
. Имеем:
 , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  ;
;
 , а
, а  , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  .
.
б)  . Имеем:
. Имеем:
 , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  ;
;
 , а
, а  , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  .
.
Пунктыв)иг) решите самостоятельно.►
Классы  ,
,  ,
,  ,
,  ,
,  называют классами Поста.
называют классами Поста.
Упражнение 2.41. Определите, каким из классов Поста принадлежат функции
а)  ; б)
; б)  .
.
◄ а)Удобно работать с функцией, заданной таблично:
 |  |  |  |  |  |  |
 , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  ;
;
 , следовательно,
, следовательно,  ;
;
 , а
, а  , следовательно,
, следовательно,  .
.
