Основные соотношения метода конечных элементов

Метод конечных элементов получил широкое распространение как эффективный инструмент решения многих прикладных задач современной техники. В отличие от метода конечных разностей, в котором приближенное решение краевой задачи ищется путем дискретизации соответствующих дифференциальных уравнений, МКЭ основан на численном решении соответствующей вариационной задачи. В вариационном исчислении доказывается эквивалентность задачи отыскания решения краевой задачи вида (1.11) – (1.13) задаче поиска функции 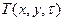, доставляющей минимум функционалу

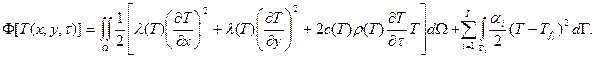(1.14)

Переменная величина Ф называется функционалом, зависящим от функции 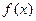( 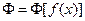), если имеет место соответствие: функции 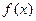соответствует число Ф.

Идея МКЭ заключается в следующем. Вся область 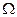разбивается на подобласти простейшей формы – конечные элементы. В случае плоской задачи в качестве конечных элементов наиболее часто используются четырехугольные и треугольные элементы. Внутри каждого элемента искомое распределение температуры ищется в виде интерполяционного полинома.

Если в качестве интерполяционного используется линейный полином вида

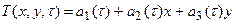, (1.15)

то соответствующий конечный элемент называется симплекс-элементом.