Ограничено, если оно ограничено как сверху, так и снизу. В противном случае, оно называетсянеограниченным.

Лекции №6. ВВЕДЕНИЕ В АНАЛИЗ. ФУНКЦИЯ

При изучении явлений природы мы на каждом шагу сталкиваемся с изменением величин, с зависимостью одной из величин от другой. Поэтому понятие о переменной величине является основным в математическом анализе.

Под переменной мы будем понимать величину, которая в процессе изучения какого-либо явления принимает хотя бы два различных значения. Величина, которая при исследовании данного вопроса принимает только одно значение, называется постоянной.

Если все значения, принимаемые переменной величиной, объединить, то мы получим множество значений этой величины.

Понятие независимой переменной величины в математике обобщается до понятия абстрактного множества, состоящего их некоторых элементов, а понятие зависимой переменной величины обобщается до понятия функции.

Множества. Логическая символика

1.1.1. Определение. Множеством называется совокупность, собрание каких-либо объектов произвольной природы. Объекты, входящие в данное множество, будем называть элементами множества.

Запись означает, что объект есть элемент множества (принадлежит множеству А); в противном случае пишут (или ). Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Æ. Запись ( содержится в ) означает, что каждый элемент множества является элементом множества В, в этом случае множество называется подмножеством множества . Множества и называются равными ( = ), если и , другими словами, множества считаются равными, если они состоят из одних и тех же элементов.

Существуют два основных способа задания (описания) множеств.

а) множество определяется непосредственным перечислением всех своих элементов т.е. записывается в виде:

б) Множество определяется как совокупность тех и только тех элементов из некоторого основного множества Т, которые обладают общим свойством a. В этом случае используется обозначение:

.

Например, есть множество всех натуральных корней данного уравнения, т.е. .

Примеры.

1. Если , то

ÆÌA

2. Множества и равны. Так как выполняются оба включения и , т.е. они состоят из одних и тех же элементов – 1,2,3.

Операции над множествами.Для множеств можно ввести операции объединения и пересечения, которые обладают свойствами, во многом аналогичными соответствующим свойствам операций сложения и умножения чисел.

1) Пусть и произвольные множества. Множество С, состоящие из всех тех элементов, которые принадлежат хотя бы одному из множеств и , называется объединением множеств и и обозначается (рис.1). Таким образом,

.

Здесь и далее символы означают «по определению».

2) Множество С_, состоящие из всех тех и только тех элементов, которые принадлежат каждому из данных множеств и называется пересечением множеств и и обозначается , т.е.

(рис.2)

Рис.1 Рис.2

Пример. и , то по определению имеем

Операции объединения и пересечения обладают следующими свойствами:

1. коммутативности:

;

2. ассоциативности:

;

3. дистрибутивности:

;

4. идемпотентности:

,

Очевидно, что Æ , Æ=Æ.

Если Æ, то будем говорить, что множества и не пересекаются.

3) Разностью множеств и называется множество , состоящее из всех элементов , которых нет в . Заметим, что в общем случае (рис.3.1). Но если , то

Рис. 3.1 Рис. 3.2

Пример. Если , то

4) Если , то разность называют дополнениеммножества А до множества и обозначают (или ). В тех случаях, когда рассматривается только подмножества некоторого основного множества , то дополнение множества до множества называют просто дополнением и пишут (или ).

Из этого определения следует, что

Æ, .

Свойства

называют законами двойственности или законами де Моргана.

Множества, элементы которых являются числами, называются числовыми. Приведём основные примеры числовых множеств.

Множество натуральных чисел обозначается через , .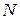

Во множестве 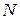действуют операции сложения и умножения.

Множество целых чисел обозначается через Z:

.

Во множестве действуют операции сложения, вычитания и умножения.

Множество рациональных чисел обозначается через ,

.

В множестве действуют все четыре арифметические операции. Множество всех действительных чисел – как рациональных, так и иррациональных, обозначается через . В нём выполняются все арифметические действия и извлекаются корни любой степени из неотрицательных чисел.

Эти множества являются подмножествами друг друга в следующем порядке:

.

1.1.2 Символика математической логики. Для сокращения записи в дальнейшем будем употреблять некоторые основные логические символы, или кванторы. Пусть a и b некоторые предложения.

1) Запись означает: “из a следует b ”, " Þ " символ импликации.

2) Запись означает “a и b эквивалентны”, т.е. что, из и из .

" Û "– символ эквивалентности.

Любую теорему в математике можно записать в виде или в виде , a – условия теоремы, а b – её утверждение.

3) Знак “"” означает: “каждый, любой, для каждого” и т. д. "– квантор общности. Например, означает: “для всякого элемента 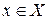истинно утверждение ”.

4) Знак “$” означает “существует, найдется, имеется”. "$"– квантор существования. $ - перевернутая - начальная буква слова “Existenz” - “существует”. Например, означает: существует элемент 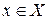такой, что для него истинно утверждение . Если элемент хиз Х, для которого истинно утверждение , не только существует, но и единствен, то пишут: .

5) Знак “:” означает: “такой, что” или “такие, что”, специального названия он не имеет.

6) Знак “ ” или означает отрицание утверждения , " " - символ отрицания. Часто при доказательстве теорем используется метод "от противного", который использует равносильность предложений ( ) и ( ).

7) Запись означает " и " ( " " – символ конъюнкции).

8) Запись означает " или " (" " – символ дизъюнкции).

1.1.3 Отрезок, интервал, ограниченное множество. Введём следующие обозначения для подмножеств в .

Множество чисел х , удовлетворяющих неравенствам , называется отрезком (с концами ) или сегментом и обозначается так:

, т.е. .

Множество чисел , удовлетворяющих неравенству , называетсяинтервалом (с концами ) или открытом отрезком и обозначается так: (а, b), т. е. (а, ) ={ : }.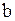

Множество чисел , удовлетворяющих неравенствам а или , обозначаются соответственно и называются полуоткрытыми отрезками илиполуинтервалами. Первый, например, закрыт слева и открыт справа.

Отрезки, интервалы и полуинтервалы называются числовыми промежутками или просто промежутками.

Произвольный интервал (а, b), содержащий точку мы будем называть окрестностью точки .

a x_{0 b}

Рис.4

В частности, интервал называют 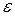- окрестностью точки

Пример. (10) =(9,9; 10,1).

Часто рассматривают множества, называемые бесконечными интервалами или полуинтервалами:

1) ( ), 2)( ], 3)( ), 4)( ), 5)[ ).

Первые их них есть множество всех действительных чисел (действительная прямая), остальные состоят их всех чисел, для которых соответственно:

2) , 3) , 4) , 5) .

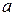Если и 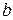конечны и , то число называетсядлиной сегмента или интервала , или полуинтервала ( .

Пусть Х есть произвольное множество действительных чисел.

Говорят, что множество X ограничено сверху, если (действительное), число М такое, что .

Ограничено снизу, если число т такое, что .

Ограничено, если оно ограничено как сверху, так и снизу. В противном случае, оно называетсянеограниченным.

Ясно, что множество Х ограничено, если , так как .

Неограниченное множество Х можно определить так: множество Хнеограниченно .

Пример. – ограниченное множество – ограничено, если 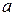и конечны, и не ограничено, если .

1.1.4 Переменные и постоянные величины.Величина называется переменной, если она принимает различные значения. Если величина все время сохраняет одно и то же численное значение, то она называется постоянной. Поскольку все в окружающем нас мире находится в непрерывном движении, изменении, ясно, что большинство величин, характеризующих происходящие в материальном мире процессы и явления, являются переменными. Что касается постоянных величин, то они могут быть постоянными всегда (например, сумма углов всякого треугольника равна 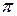) либо только в данном процессе, в другом процессе они могут оказаться переменными (например, автомобиль может двигаться с постоянной скоростью и с меняющейся скоростью ). В математическом анализе постоянные величины рассматриваются как частный случай переменных величин: это такие «переменные», которые всегда или, по крайней мере, в данном процессе принимают одно и то же значение.

Область значений переменной величины.Множество всех значений переменной величины составляет ее область значений. Областью значений переменной часто бывает интервал.

Пример.Точка М (рис. 5) движется по окружности радиуса г = 1 с центром в начале координат.

M

Рис. 5

1 1

Рис. 5

Если считать, что точка совершила, по крайней мере, один полный оборот, то область значений ее абсциссы есть замкнутый интервал [-1;1]. Если движение началось с положения , происходит против часовой стрелки и сделано полных оборотов, то область значений переменной величины 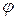- некоторый интервал . Область значений переменной есть .

Однако областями значений переменных величин могут быть и другие множества, отличные от интервалов и их объединений. Например, если -количество деталей, изготовленных рабочим за смену, то может принимать лишь целые и неотрицательные значения, но не . Область значений этой переменной величины не является интервалом.

Часто важно знать не только область значений переменной, но и в каком порядке переменная принимает значения: какие из этих значений принимаются раньше, а какие позже.

Пример. Вернемся к Рис.5. Если точка 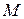совершает половину оборота против часовой стрелки, т.е. от до , то убывает от 1 до -1. Область значений - интервал

[-1;1], пробегаемый справа налево.

Если же точка 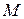совершает половину оборота от до : , то взрастает от -1 до +1, и область значений [-1;1] пробегается слева направо.

Если точка 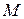делает один полный оборот, то область значений - все тот же интервал

[-1;1], но он пробегается дважды.

Далеко не для всех типов переменных величин бывает просто указать, какое из их значений какому предшествует и за каким следует. Однако этот вопрос просто и естественно решается для одного важного класса переменных величин - так называемых последовательностей.

Последовательности.Предположим, что все значения, принимаемые переменной величиной , можно пронумеровать с помощью всевозможных натуральных (целых положительных) чисел: причем значение с большим номером принимается после значения с меньшим номером: если , то значение предшествует значению , в частности предшествует . В этом случае говорят, что переменная пробегает последовательность значений или что имеется последовательность (или числовая последовательность). Числа называются членами последовательности: - первый член, , - второй и т.д. Число с произвольным номером 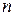называется общим членом последовательности. Последовательность определена, если мы знаем закон, по которому для любого номера 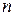образован соответствующий член последовательности. Иными словами, если мы знаем закон зависимости общего члена от его номера 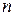. Последовательность часто обозначают

Примеры:

1.

2.

3.

4.

Мы видим, что члены последовательности не обязаны все быть разными числами: область значений последовательности в примере 3 состоит из значений: -1 и 1. Переменная, пробегающая последовательность в примере 4 оказывается на самом деле постоянной.