Методические указания к решению задачи № 1.3

В задаче № 1.3 рассматривается статически неопределимая конструкция, стержневые элементы которой работают на растяжение или сжатие и число неизвестных сил, приложенных к абсолютно жесткому брусу, превышает возможное число уравнений статики. Разность между числом неизвестных усилий и числом возможных уравнений статики определяет степень статической неопределимости системы:

,

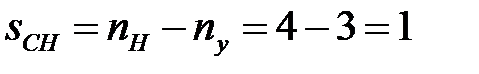где n_H – число неизвестных сил; n_y – число уравнений статического равновесия.

Уравнения, недостающие для определения усилий в стержнях, можно получить, рассматривая возможную деформацию системы. Условие, выражающее зависимость между деформациями отдельных элементов системы (конструкции), называется условием совместности деформаций. Оно получается из геометрических соотно­шений между дефор­мациями элементов конструкции. Используемые при решении задачи расчетные формулы приведены в методических указаниях к решению задач № 1.1 и 1.2 (см. раздел 2.3) .

Статически неопределимые конструкции рассчитывают, рассматривая совместно уравнения статической, геометрической и физической сторон задачи. При этом придерживаются следующего порядка:

1. Статическая сторона задачи. Составляются уравнения равновесия отсеченных элементов конструкции, содержащие неизвестные усилия. Определяется степень статической неопределимости.

2. Геометрическая сторона задачи. Рассматривая систему в деформированном состоянии, устанавливаются чисто геометрические связи между деформациями и перемещениями отдельных элементов конструкции и составляются уравнения совместности деформаций (уравнения совместности перемещений). Для получения этих уравнений используются прямой и обратный методы засечек (см. раздел 2.3).

3. Физическая сторона задачи. На основании закона Гука выражаются перемещения или деформации элементов конструкции через действующие в них неизвестные (пока) усилия.

4. Математическая сторона задачи (синтез). Решая совместно статические, геометрические и физические уравнения, находят неизвестные усилия.

Для определения температурных напряжений и монтажных усилий указанная схема расчета сохраняется. В этих случаях условия статики составляют только для усилий стержней.

Величины изменений длин нагретых или охлажденных элементов определяют алгебраическим суммированием приращений длин от усилий 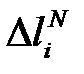и изменения температуры :

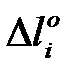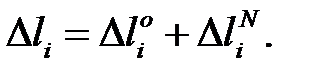
Абсолютное удлинение стержня от продольной силы определяется законом Гука

.

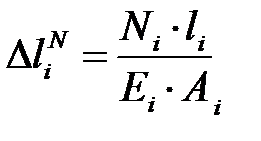Абсолютное удлинение стержня от изменения температуры Δt определяется зависимостью вида:

,

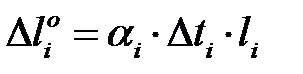где α_i - коэффициент температурного расширения.

Пример решения задачи 1.3

Дано: расчетная схема шарнирно - стержневой системы, представленная на рисунке 2.7.

F=100 кН, а = 1,2 м, b = 0,8 м; материал – сталь: модуль упругости Е = 2×10⁵ МПа, допускаемое напряжение [σ]= 100 МПа, коэффициент температурного расширения α = 12,5×10^-6 1/градус.

Требуется определить:

1) размеры квадратного поперечного сечения стержней при действии силы F, при условии, что поперечное сечение одного из стержней в два раза больше, чем другого;

2) напряжения в стержнях:

☺ от действия силы F;

☺ от неточности монтажа, если считать, что один из стержней выполнен короче на величину Δ= 0,2 мм;

☺ от изменения температуры на Δt= 20°С.

Решение:

А. Определение необходимой по условию прочности площади поперечного сечения стержней и фактических напряжений при действии силы F

1) Степень статической неопределимости.

Освободим жесткую балку AD от внешних связей, заменив их неизвестными реакциями в шарнире A и продольными усилиями стержней N1и N2 (рисунок 2.7).

Рисунок 2.6 – Шарнирно – стержневая система

,

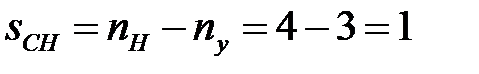где n_H =4 – число неизвестных сил; n_y=3 – число уравнений статического равновесия.

Система один раз статически неопределима.

2) Раскрытие статической неопределимости – определение продольных сил в упругих стержнях.

Статическая сторона задачи.

Составляем уравнения статического равновесия, т.к. реакции определять ненужно, то остается одно уравнение:

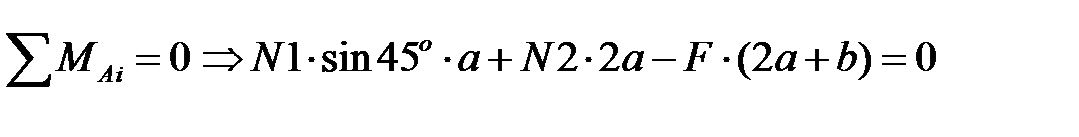
или 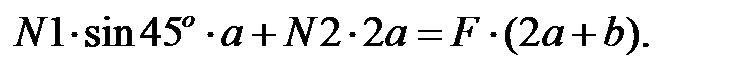(1)

Геометрическая сторона задачи.

Составляем деформированную схему системы и сопоставляя ее с исходной имеем (рисунок 2.7):

а) исходная и деформированная схемы системы; б) деформация стержня I

Рисунок 2.7

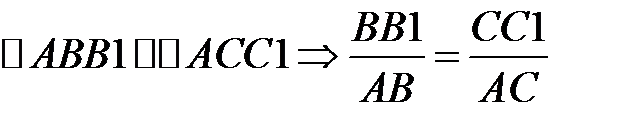
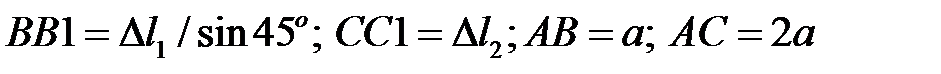
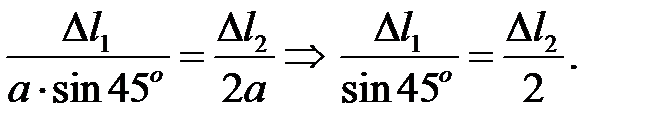(2)

Физическая сторона задачи.

Согласно закону Гука можно записать

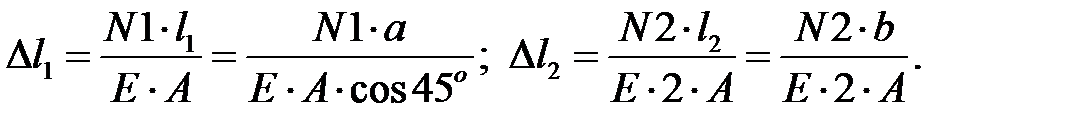(3)

Синтез решения.

Подставляя выражение физической стороны задачи (3) в выражение из геометрической стороны задачи (2) и преобразуя, имеем:

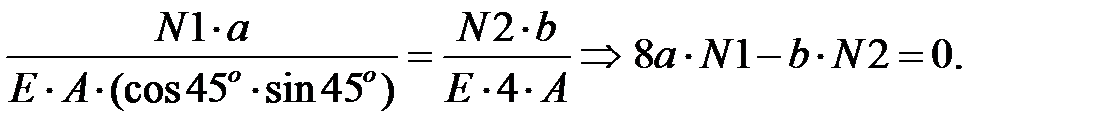(4)

Составляем систему уравнений из полученного выражения (4) и уравнения моментов из статической стороны задачи (1)

.

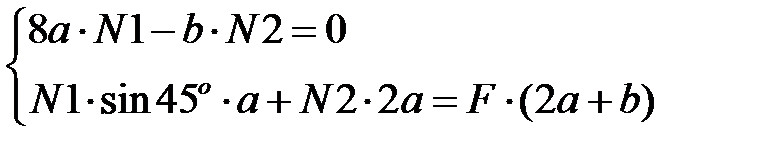Решая эту систему с известными исходными данными, получаем:

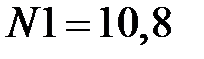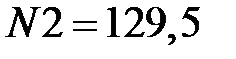кН; кН.

3) Определение площадей поперечного сечения стержней

Определим, какой из стержней нагружен сильнее. По закону Гука

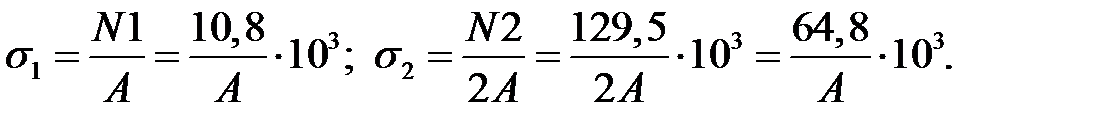
Второй стержень является более нагруженным, так как σ₁< σ₂, поэтому определим площадь поперечного сечения по условию прочности для стержня 2

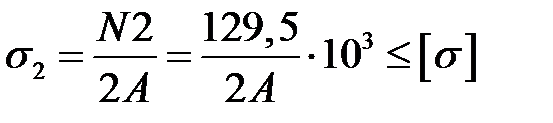
или

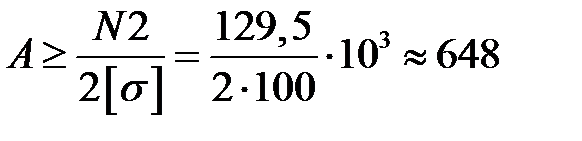мм².

Сторона квадрата сечения 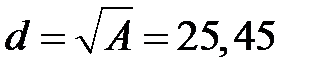мм.

Подбираем размер по ГОСТ6636-69 (приложение С4) d=26 мм. Тогда, A= 676мм².

4) Определение фактических напряжений в стержнях от внешних сил

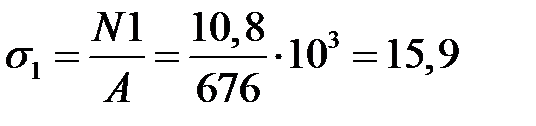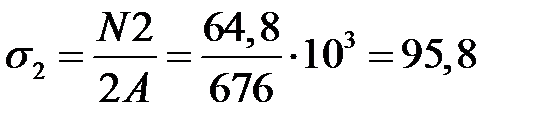МПа;

МПа.

Первый стержень работает на сжатие, а второй – на растяжение.

В. Определение фактических напряжений от неточности монтажа

Будем считать, что короткий стержень выполнен короче на величину Δ= 0,2 мм, сила - F отсутствует (см. рисунок 2.8).

Статическая сторона задачи.

Составляем уравнения статического равновесия, т.к. реакции определять ненужно, то остается одно уравнение:

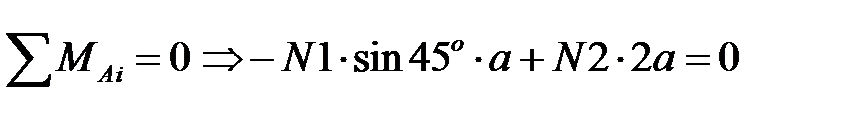
или 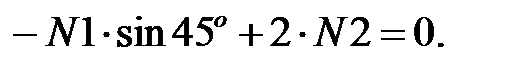(5)

Геометрическая сторона задачи

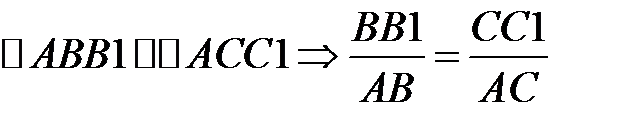
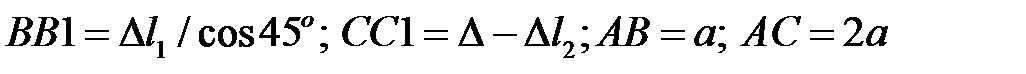
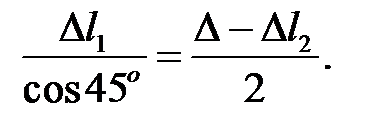(6)

Рисунок 2.8

Физическая сторона задачи

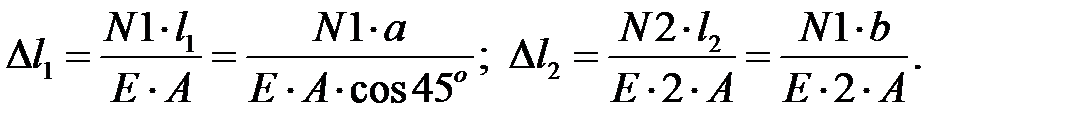(7)

Синтез

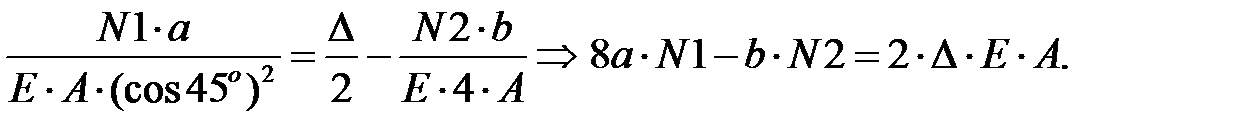(8)

Составляем систему уравнений из полученного выражения (8) и уравнения моментов из статической стороны задачи (5)

.

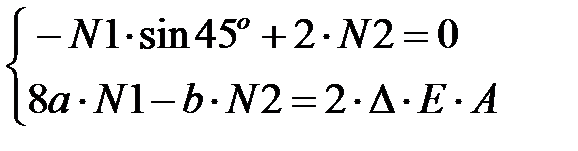Решая эту систему с известными исходными данными, получаем:

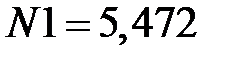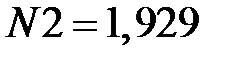кН; кН

Определение фактических напряжений в стержнях от монтажных неточностей

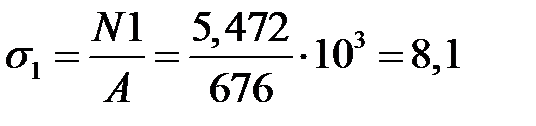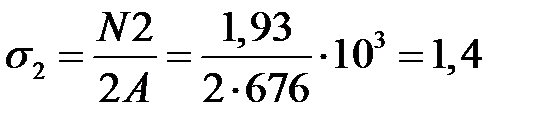МПа;

МПа.

Оба стержня работают на растяжение.

С. Определение фактических напряжений от изменения температуры.

Будем считать, что температура системы повышается. Тогда оба стержня будут удлиняться от повышения температуры. При удлинении стержней, они будут воздействовать друг на друга через недеформируемый стержень АС. Вследствие этого, в обоих стержнях будут возникать дополнительные силы сжатия (рисунок 2.9).

Рисунок 2.9

Статическая сторона задачи.

Составляем уравнения статического равновесия, т.к. реакции определять ненужно, то остается одно уравнение:

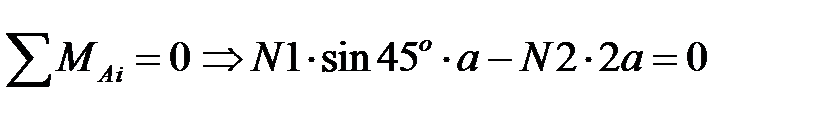
или 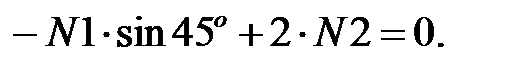(9)

Геометрическая сторона задачи

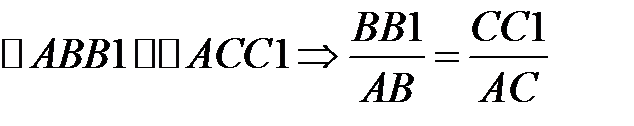
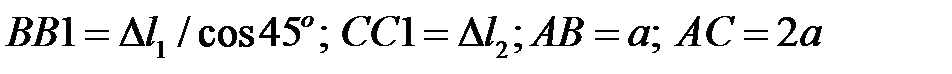
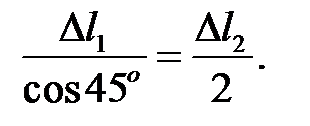(10)

Физическая сторона задачи.

Согласно закону Гука можно записать

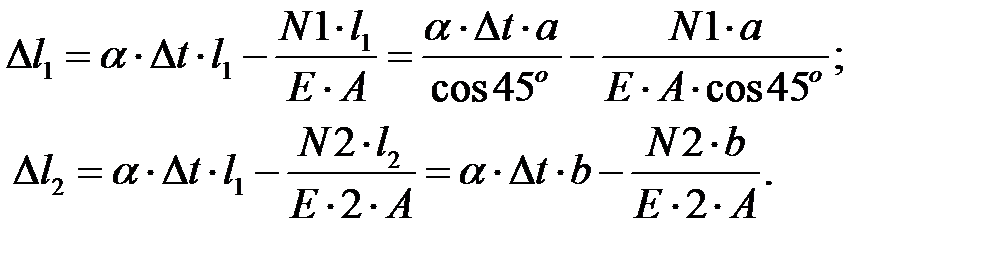(11)

Синтез

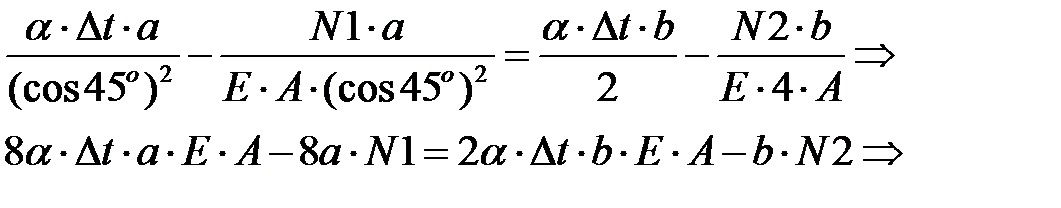
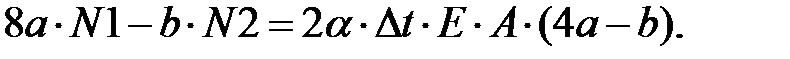(12)

Составляем систему уравнений из полученного выражения (12) и уравнения моментов из статической стороны задачи (9)

.

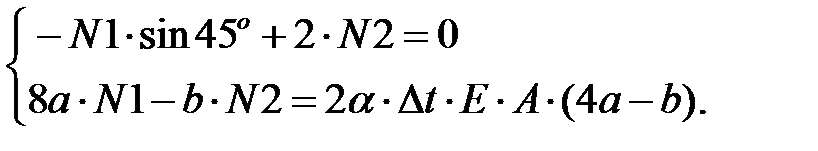Решая эту систему с известными исходными данными, получаем:

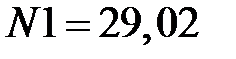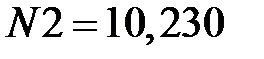кН; кН

Определение фактических напряжений в стержнях от нагрева

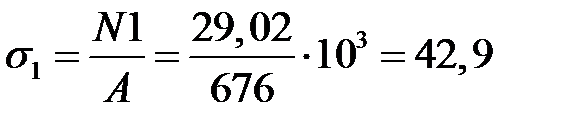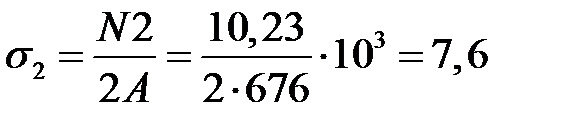МПа;

МПа.

Оба стержня работают на сжатие.

Вопросы для письменного ответа

1. Что такое продольная (нормальная) сила?

2. Cущность метода сечений.

3. Виды деформаций и какими силовыми факторами они вызываются?

4. Как формулируется и записывается закон Гука для участка стержня при растяжении (сжатии)?

5. Что называется прочностью, жесткостью и устойчивостью конструкции?

Варианты тестовых заданий

2.1	Восстановить внешнюю силу F2 по заданной эпюре продольной силы	2.2	Восстановить внешнюю силу F3 по заданной эпюре продольной силы
2.3	На диаграмме деформирования укажите упругую составляющую деформации	2.4	Для заданного стержня постоянного сечения площадью А определить соотношение между силами F2 и F1 , если задана эпюра перемещений. Модуль Юнга материала – Е.
2.5	Для заданного стержня постоянного сечения площадью А определить sмах по абсолютному значению	2.6	Для заданного стержня постоянного сечения площадью А определить продольное перемещение сечения I. Модуль Юнга материала – Е
2.7	Для заданного стержня постоянного сечения площадью А определить полное продольное перемещение. Модуль Юнга материала – Е.	2.8	На условной диаграмме деформирования укажите предел текучести материала
2.9	Для заданного стержня постоянного сечения площадью А определить силу F1 , необходимую для выбора монтажного зазора δ. Модуль Юнга материала (Е) задан.	2.10	Для заданного стержня постоянного сечения площадью А определить соотношение между силами F и F1, если полное продольное перемещение Δl=0 и Е∙ А=const . Е - модуль Юнга материала.