II. Методика эксперимента
Лабораторная работа № 12.
Изучение колебательного движения (физический маятник).
Цель работы: изучение колебательного движения на примере гармонических колебаний физического маятника, определение его приведённой длины и момента инерции, измерение ускорения свободного падения.
I. Основные понятия и определения.
Колебательное движение, являясь одним из основных видов движения, характеризуется повторяемостью координаты, скорости, ускорения через строго определённые промежутки времени, минимальная величина которых называется периодом и обозначается T.
Простейшими являются гармонические колебания, для которых координата, скорость и ускорение зависят от времени по закону синуса и косинуса, например, 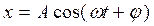 . Здесь
. Здесь 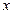 - координата колеблющейся точки,
- координата колеблющейся точки, 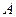 - амплитуда колебаний (максимальное отклонение от положения равновесия),
- амплитуда колебаний (максимальное отклонение от положения равновесия), 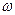 - угловая частота колебаний,
- угловая частота колебаний, 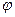 - начальная фаза колебаний. Угловая частота колебаний связана с периодом T соотношением
- начальная фаза колебаний. Угловая частота колебаний связана с периодом T соотношением 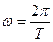 .
.
Для наглядности любое гармоническое колебание можно представить вращением вектора величиной 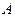 с частотой
с частотой 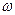 от начального угла
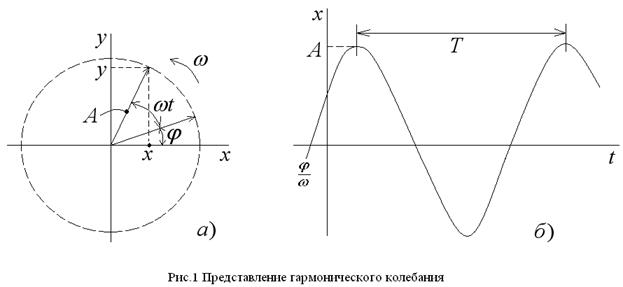
от начального угла 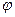 вокруг начала координат, как на рис. 1(а), тогда проекции конца вектора будут зависеть от времени по гармоническому закону. Зависимость координаты от времени, приведённая на рис 1(б), представляет собой синусоиду (косинусоиду), смещённую относительно начала отсчёта на величину
вокруг начала координат, как на рис. 1(а), тогда проекции конца вектора будут зависеть от времени по гармоническому закону. Зависимость координаты от времени, приведённая на рис 1(б), представляет собой синусоиду (косинусоиду), смещённую относительно начала отсчёта на величину 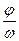 .
.
Для скорости и ускорения колебательного движения легко получить выражение, дифференцируя зависимость координаты колебаний по времени:
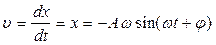 ;
; 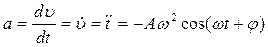 .
.
Уравнение Ньютона 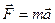 является уравнением любого механического движения, поэтому, подставляя в уравнение найденное значение ускорения, получим для силы выражение вида
является уравнением любого механического движения, поэтому, подставляя в уравнение найденное значение ускорения, получим для силы выражение вида 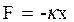 , где
, где 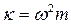 - упругая постоянная. Сила
- упругая постоянная. Сила 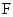 называется квазиупругой или возвращающей к положению равновесия силой. Таким образом, гармонические колебания совершаются только под действием квазиупругой силы.
называется квазиупругой или возвращающей к положению равновесия силой. Таким образом, гармонические колебания совершаются только под действием квазиупругой силы.
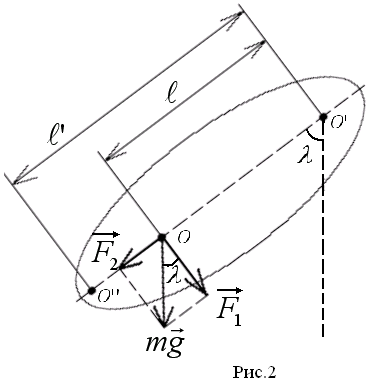
Весьма распространённым инструментом для изучения колебаний являются маятники. Под физическим маятником понимается любое тело, ось вращения которого не проходит через центр инерции, как изображено на рис.2. На маятник действует сила тяжести 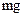 , создающая вращающий момент
, создающая вращающий момент 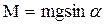 , где
, где 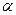 - угол отклонения маятника от положения равновесия. Согласно основному уравнению вращательного движения
- угол отклонения маятника от положения равновесия. Согласно основному уравнению вращательного движения 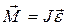 , где
, где 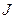 - момент инерции тела,
- момент инерции тела, 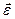 - угловое ускорение,
- угловое ускорение, 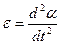 , уравнение колебаний физического маятника запишется в виде:
, уравнение колебаний физического маятника запишется в виде:
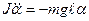 . (12.1)
. (12.1)
Здесь использовано условие малости угла отклонения и замена 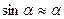 - условие гармоничности колебания.
- условие гармоничности колебания.
Таким образом, уравнение (12.1) будет являться уравнением гармоничности колебания (угол 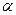 гармонически зависит от времени), если положить, что частота и период колебаний должны определяться выражением:
гармонически зависит от времени), если положить, что частота и период колебаний должны определяться выражением:
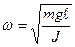 ;
;
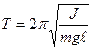 . (12.2).
. (12.2).
Из выражения (12.2) следует, что частота колебаний определяется моментом инерции, т.е. распределением масс по объёму маятника, а не только его массой и положением точки подвеса 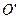 .
.
Ситуацию можно упростить, если предположить, что вся масса маятника сосредоточена в его центре инерции 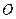 . Тогда его момент инерции будет равен
. Тогда его момент инерции будет равен 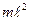 и частота колебаний
и частота колебаний
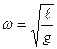 . (12.3)
. (12.3)
Маятник, представляющий собой материальную точку, подвешенную на длинной, тонкой, нерастяжимой нити, называется математическим. Его частота колебаний определяется только длиной нити.
Выражение (12.3) также можно представить в виде, аналогичном для математического маятника, если ввести понятие приведённой длины физического маятника 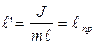 . Оказывается на расстоянии приведённой длины от точки подвеса
. Оказывается на расстоянии приведённой длины от точки подвеса 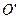 расположенная сопряжённая ей точка
расположенная сопряжённая ей точка 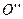 . Сопряжённые точки
. Сопряжённые точки 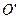 и
и 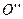 примечательны тем, что частоты (периоды) колебаний маятника относительно оси проходящей через точку
примечательны тем, что частоты (периоды) колебаний маятника относительно оси проходящей через точку 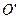 и
и 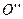 одинаковы.
одинаковы.
Если действуют силы трения, то уравнение движения колеблющейся точки 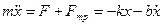 , где b – коэффициент пропорциональности. Энергия затухающих колебаний
, где b – коэффициент пропорциональности. Энергия затухающих колебаний 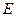 убывает. Если величина b мала, то уменьшение энергии колебаний:
убывает. Если величина b мала, то уменьшение энергии колебаний: 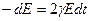 . Здесь
. Здесь 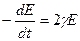 - мощность потерь. Отсюда решая дифференциальное уравнение, получим
- мощность потерь. Отсюда решая дифференциальное уравнение, получим 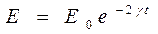 . Учитывая, что
. Учитывая, что 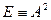 , для амплитуды затухающих колебаний получим
, для амплитуды затухающих колебаний получим 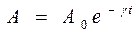 , где
, где 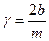 - постоянная затухания.
- постоянная затухания.
Величина затухания колебаний за период называется логарифмическим декрементом затухания 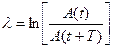 . Величина, равная отношению энергии колебаний к мощности потерь за время
. Величина, равная отношению энергии колебаний к мощности потерь за время 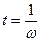 , называется добротностью колебательной системы
, называется добротностью колебательной системы 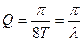 . Таким образом, добротность равна числу колебаний за время, в течение которого амплитуда убывает в
. Таким образом, добротность равна числу колебаний за время, в течение которого амплитуда убывает в 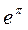 раз, а энергия – в
раз, а энергия – в 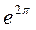 раз.
раз.
II. Методика эксперимента.
В установке используется оборотный физический маятник с двумя подвижными опорами качания 1 и 2 и двумя одинаковыми грузами 3 и 4, которые могут перемещаться по штанге 5 (рис. 12.3). Крепление опор качания и грузов, осуществляется винтами. Фотоэлектрический датчик 6 в автоматическом режиме фиксирует 50 полных колебаний, которые регистрируются секундомером. Запуск схемы регистрации осуществляется штангой 5 при первом колебании. При этом установка секундомера осуществляется кнопкой “СТОП” на панели электронного блока. Цепь измерений заключается в определении длины физического маятника при малых колебаниях – угол отклонения 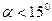 . Для этого необходимо провести следующие измерения с занесением результатов в таблицу.
. Для этого необходимо провести следующие измерения с занесением результатов в таблицу.
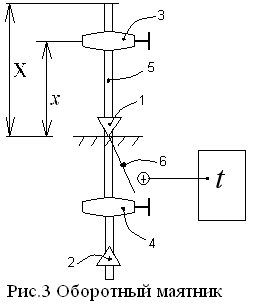
1. Установить груз 3 с помощью фиксирующего винта 7 в положение 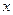 и зарегистрировать
и зарегистрировать 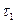 - время 50 полных колебаний.
- время 50 полных колебаний.
2. Не изменяя точки опоры маятника, передвинуть груз 3 в новое положение и снова зарегистрировать время.
3. Построить зависимость времени колебаний маятника на опоре 1 от положения груза 3 (кривая 1 на рис.4).
4. Перевернуть маятник и подвесить его за опору 2 и проделать измерения по пунктам 1,2,3, снова перемещая груз 3. Построить зависимость времени колебания маятника 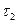 на опоре 2 от положения груза 3 (кривая 2 на рис.4).
на опоре 2 от положения груза 3 (кривая 2 на рис.4).
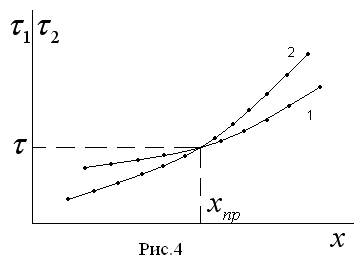
5. По точке пересечения графиков найти положение груза, при котором периоды оборотного маятника совпадают.
6. Установить груз 3 в положение 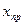 и определить время 50 колебаний поворотного маятника на опорах 1,
и определить время 50 колебаний поворотного маятника на опорах 1, 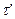 и 2,
и 2, 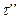 :
: 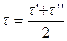 .
.
7. Определить период колебаний 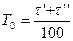 . Найти средний период колебаний
. Найти средний период колебаний 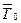 и занести в табл.12.1.
и занести в табл.12.1.
Определить доверительный интервал измерения 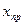 и
и 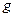 ,
,
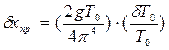 ,
,
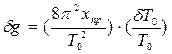 .
.
