Дайте определение арксинуса числа. Приведите примеры.

Арксинус числа х (arcsin(x))- это такой угол 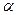из промежутка 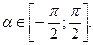, синус которого равен .

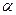17. Дайте определение функции y=arcsinx.

у = arcsin(x)-это функция, обратная к функции у = sin(x).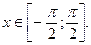

18. Перечислите основные свойства функции y=arcsinx.

Свойства функции:

1. D(arcsin x)= .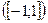

2. E(arcsin x)= .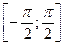

3. у = arcsin(x)-является нечетной функцией( также как у = sin(x)).

arcsin(-x)=- arcsin(x)

4. Функция у=arcsin(x)-является строго возрастающей.

5. sin(arcsin x)=x ; ;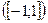

arcsin(sin(y))=y, .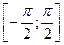

6.Нуль функции. При у=0 ,х=0 так как arcsinx=0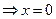

arccos x + arcsin x=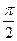

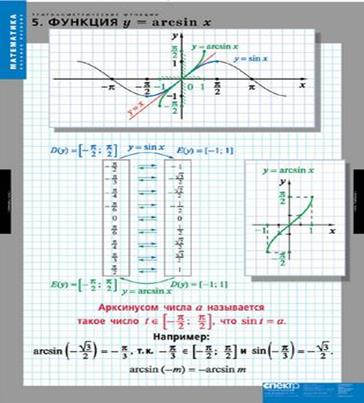
19. Покажите как строится график функции y=arcsinx.

Пусть 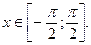На этом отрезке у = sin(x) строго монотонно возрастает и пробегает все значения из области значений синуса 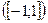только один раз, значит, для функции у = sin(x) на отрезке 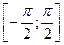существует обратная, которая обозначается у=arcsin(x), график которой симметричен графику функции у = sin(x) на отрезке 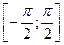относительно прямой у=х.

Дайте определение арккосинуса числа. Приведите примеры.

Арккосинус числа х (arccos(x))- это такой угол 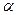из промежутка 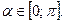, косинус которого равен .

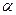21. Дайте определение функции y=arccosx.

у = arccos (x)-это функция, обратная к функции у = cos (x) на .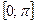

22. Перечислите основные свойства функции y=arccosx.

Свойства функции:

1. D(arccos x)= .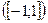

2. E(arccos x)= .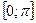

3. у = arccos (x)-является функцией общего вида ( в отличае, от у = cos (x)).

arccos (-x)= 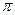- arccos (x)

4. Функция у=arccos (x)-является строго убывающей.

5. cos (arccos x)=x ; ;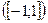

arccos (cos (y))=y, .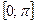

6. Нуль функции. При у=0 ,х=1 так как arccosx=0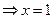

arccos x + arcsin x= .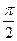

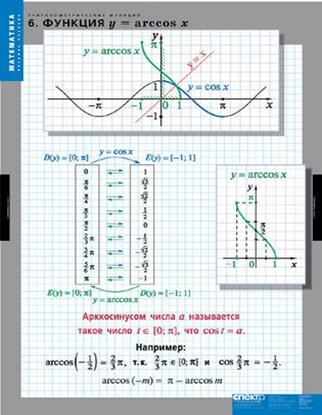
23. Покажите как строится график функции y=arccosx.

Пусть 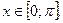На этом отрезке у = cos(x) строго монотонно возрастает и пробегает все значения из области значений синуса 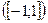только один раз, значит, для функции у = cos(x) на отрезке 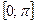существует обратная, которая обозначается у=arccos(x), график которой симметричен графику функции у = cos (x) на отрезке 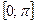относительно прямой у=х.

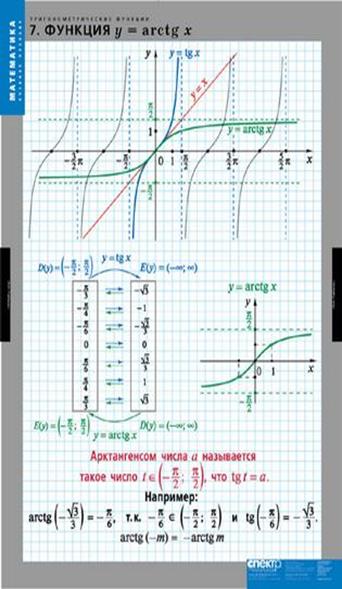
Дайте определение арктангенса числа. Приведите примеры.

Арктангенсом числа х (arctg(x))- это такой угол 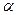из промежутка 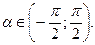, тангенс которого равен .

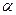25. Дайте определение функции y=arctgx.

у = arctg (x)-это функция, обратная к функции у = tg(x) на .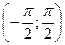

26. Перечислите основные свойства функции y=arctgx.

Свойства функции:

1. D(arctg x)= .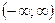

2. E(arctg x)= .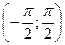

3. у = arctg (x) - нечетная функция ( как и у = tg (x)).

arctg (-x)= - arctg (x)

4. Функция у=arctg (x) - является строго возрастающая.

5. tg (arctg x)=x ; ;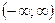

arctg (tg (y))=y, .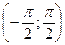

6. Нуль функции. При у=0 ,х=0 так как arctgx=0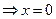

27. Покажите как строится график функции y=arctgx.

Пусть 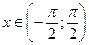. На этом отрезке у = tg(x) строго монотонно возрастает и пробегает все значения из области значений тангенса 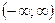только один раз, значит, для функции у = tg(x) на 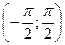существует обратная, которая обозначается у = arctg(x), график которой симметричен графику функции у = tg (x) на отрезке 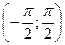относительно прямой у=х.