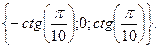Жаңа белгісіз енгізу тәсілі

Келтірілген теңдеулердің әрқайсысын түрлендіру көмегімен х функциясы болатын жаңа белгісізге қарағанда басқа теңдеуге келтіруге болады. Оны шешіп, бастапқы белгісіз х-ке көшу керек. Кейбір оқушылар соңғы теңдеуден жаңа белгісізді табумен шектеледі де одан арылмайды. Шешуді ақырына дейін жеткізбейді, сақ болу керек.

Бұл теңдеулердің бір түрлі тәсілмен шешілетінін қайдан білдік? Біріншіден, олардың түр ұқсастығы, екіншіден дәреже негіздерінің ұқсастығы не бірдейлігі, көпмүшелердің симметриялығы немесе белгісізі бар мүшелердің бірдейлігі. Теңдеулерді шешуге нұсқайық.

Мысалы, 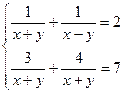теңдеулер жүйесін шешу керек.

Шешуі: жаңа айнымалы енгізу әдісімен шешейік.

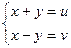белгілеп,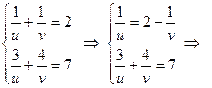

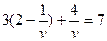
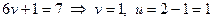
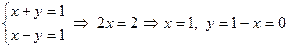
Жауабы: (0;1)

Мысалы, 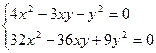теңдеулер жүйесін шешу керек.

Шешуі: Бұл жүйені шешу үшін 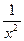көбейту керек.

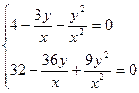теңдеулер жүйесін аламыз. Жаңа айнымалыны келесі түрде енгізіеміз: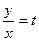

1)

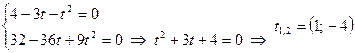
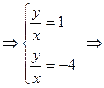
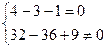
2)

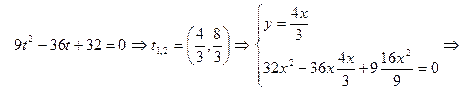
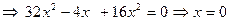
Жауабы: шешімі жоқ.

Мысалы, 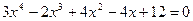теңдеуін шешу керек болсын.

Шешуі: Теңдеуді 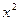-қа бөлеміз.

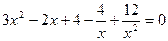
Ұқсас мүшелерін біріктіру арқылы мына түрге келтіреміз:

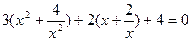
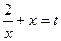айнымалысын енгізу арқылы қарапайым түрге келтіреміз.

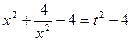
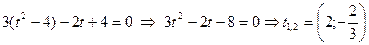
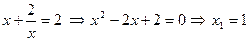
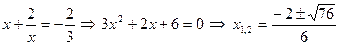
Орнына қойып тексереміз: 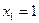болғанда, теңдеудің шешімі жоқ.

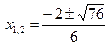болғанда да , теңдеудің шешімі жоқ.

.

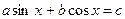
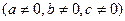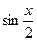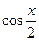түріндегі теңдеулер. Бұл теңдеулерді және -ге қарағанда біртекті теңдеулерге келтіруге болады. Немесе 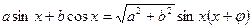формуласын пайдаланып шешуге болады, мұндағы .

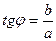Мысалы, 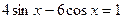теңдеуді шешу керек. Жарты аргумент функцияларға көшсек,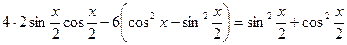

Немесе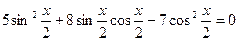

бұл біртекті теңдеу, 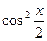-ге

бөлгенде 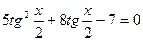бұдан табатынымыз: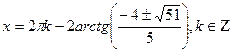

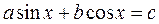теңдеуінд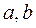е және 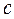-кез келген нақты сандар.

Егер 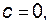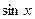және 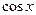-ке қарағанда біртекті теңдеулер.

теңдеуі бірінші дәрежелі біртекті теңдеу деп аталады. Бұл теңдеудің екі бөлігін де 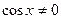деп бөлсек, 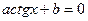осы теңдеудің түбірін табамыз.

Егер 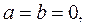ал 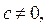онда теңдеудің мәні болмайды; егер 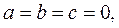онда x–кез келген нақты сан, яғни теңдеу теңдікке айналады. Мысалы 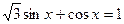қарастырамыз. Теңдеудің екі жағын 2-ге бөліп, 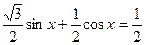яғни 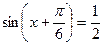немесе .

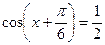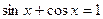теңдеуін төрт тәсілмен шешуге болады. Мысалы, теңдеудің екі жағын да 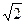-ге бөліп,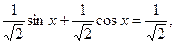 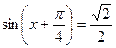теңдеуін аламыз және т.б. Кез келген коэфиценті бар 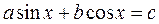теңдеуін қарастырамыз. Мұндай теңдеулер әр түрлі жолдармен шығарылады.

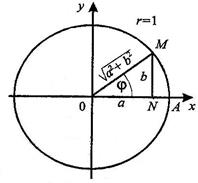
1-тәсіл: 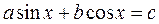теңдеуін қос бұрыш енгізу әдісі арқылы шешу.

Біз білеміз, егер 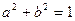болса, 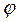бұрышы болады, 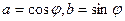немесе керісінше. 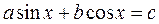теңдеуін шешу үшін 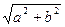көбейткішін жақша сыртына шығарамыз. Сонда 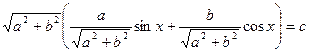теңдеуін аламыз. 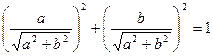болғандықтан, бірінші 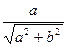санды кейбір

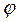бұрышының косинусы деп қабылдап, ал екінші 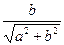сол

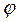бұрышының синусымен алмастырып жазамыз, яғни 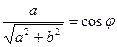, 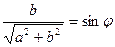. Мұндай жағдайда теңдеу 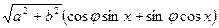немесе 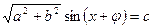түріне келеді, бұдан 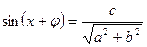. Бұл теңдеудің шешімі болады, егер 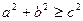, сонда , .

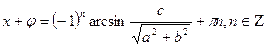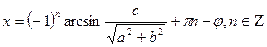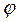бұрышы 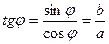теңдігінен табылады, .

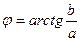Жауабы: .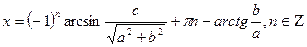

Қарастырылып өткен тәсіл 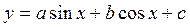функциясының max, min нүктелерін тапқанда жиі қолданылады.

Мысалы: 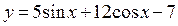функциясының max, min нүктелерін табу.

Шешуі: .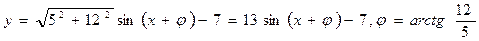

Максимум 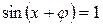болады, яғни 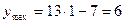. Ал 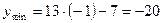болатынын көру оңай.

Жауабы: , .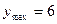

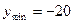Қарастырылған тәсіл 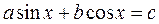теңдеуінде универсалды болып қарастырылады. Ол сонымен қатар физикада гармониялық тербелістерді қосуда қолданылады.

2-тәсіл: 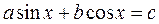– теңдеуін рационалдау әдісімен шешу.

Белгілі, егер 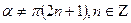, онда 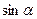, 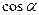және 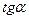, 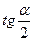арқылы рационалды өрнектеледі, яғни 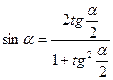, 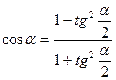және 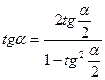. Рационалдау әдісі мыналардан қорытылады: алмастырудан кейін рационалды теңдеу белгісіз көмекшімен салыстыруға болатын, белгісіз көмекші ендіреміз. 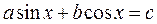теңдеуін қарастырамыз, бұдан 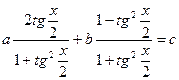теңдеуін аламыз. 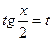деп алсақ, онда 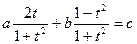аламыз. Бұл теңдеу- рационалды салыстырмалы .

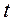Теңдеудің екі бөлігін 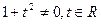көбейтеміз, сонда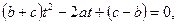 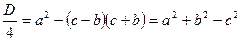болады. 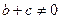немесе 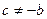деп көрсек, 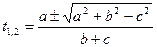болады. 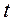мәні –нақты, егер 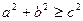. Егер 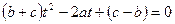теңдеуінде 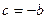деп алсақ, ендеше ол бірінші дәрежелі теңдеуге айналады: 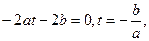яғни 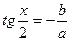, 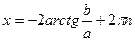. 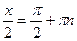болғанда, 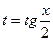өрнегі көмекші белгісізге мәнін жоғалтады, яғни 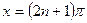. 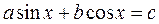теңдеудің шешімі 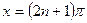жоғалуы мүмкін. 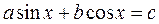теңдеуді 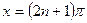алмастыру арқылы: ; .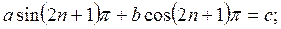

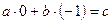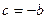Мұндай жағдайда 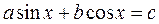теңдеу 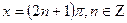түріндегі шешімдер жиыны көп болады.

1. Егер 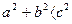болса, онда 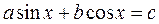теңдеудің шешімі болмайды, 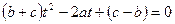теңдеудің нақты түбірлері болмағандықтан.

2. Егер 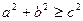және 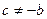болса, онда 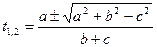теңдеуден 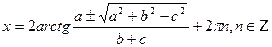табамыз.

3. Егер 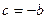, онда 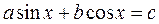теңдеудің 2 шешімі бар: 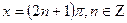және .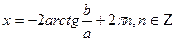

Мысалы, теңдеуді шешіңдер.

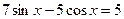
Бұл теңдеуді көмекші бұрыш ендіру арқылы шешуге де болады. 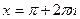деп алып, төмендегі 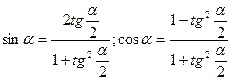формулалардың көмегімен түрлендірсек, 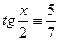. Бұл арадан 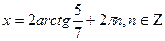. Енді 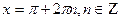мәні берілген теңдеуді қанағаттандыратынын тексерелік.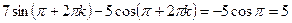

Сонымен теңдеудің шешімі:

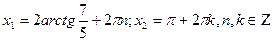
3-тәсіл: 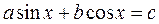теңдеуін шешу әдісі. Теңдеудің екі бөлігін де квадраттау тәсілімен, біртекті теңдеуін аламыз. Бөгде түбір шығатындықтан, бұл әдіс ең жиі қолданылатын әдіс.

Мысалы, теңдеуді шешіңдер.

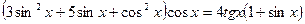
Теңдеуді анықталу облысына 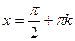мәні енбейді. Берілген теңдеу тек 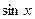-ке тәуелді, өйткені оны түрлендірсек, 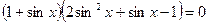түріндегі теңдеуді аламыз. Анықталу облысын ескерсек, 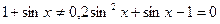.Теңдеуді 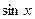-ке қатысты шешсек, бірінші түбір теңдеудің анықталу облысына енбейді, ал екіншісінен .

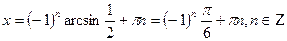Барлық тригонометриялық функциялар қатысатын теңдеулерді көбінесе 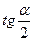арқылы өрнектеуге болады. Теңдеулерді бұл метод пен шешкенде көбінесе 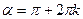түбірді жоғалтуымыз мүмкін. Сондықтан шешімді тексеру қажет. Бұл методты Эйлер методына алмастыруы деп атайды.

4-тәсіл: 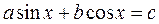теңдеуін шешу әдісі.

Теңдеуді мына түрде жазып аламыз: 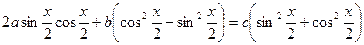,яғн 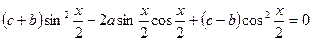және т.б. түріндегі біртекті теңдеуін аламыз:

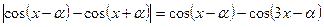немесе

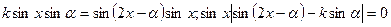
а)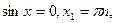

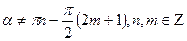
б)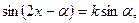

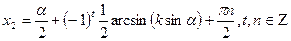
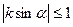
Мысалы,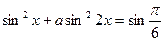

Теңдеу мына функцияға қатысты квадраттық теңдеуге айналады

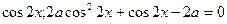, осыдан

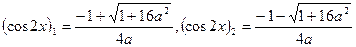
а) 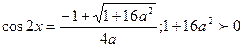әрқашан, сонымен қатар 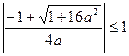болуы тиіс. Теңсіздікті шеше отырып, а- кез келген нақты сан екенін аламыз.

б) 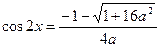. 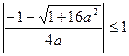теңсіздігі а-ның ешқандай мәнінде орындалмайды.

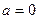болғандағы ерекше жағдай! Тендеу келесі түрге келеді: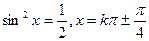

Жауабы: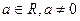

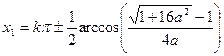
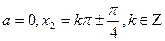
Мысалы,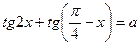

Шешуі:

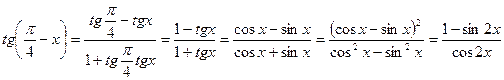. Тендеу мына түрге түрленеді:

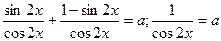яғни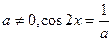

Егер

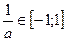
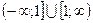, онда соңғы теңдеу мынандай шешімін табады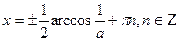

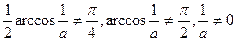
Жауабы: .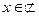

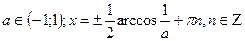
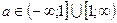Мысалы, 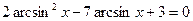теңдеуін шешейік.

Шешуі: Айнымалы енгіземіз: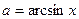

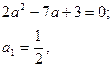
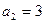- шартты қанағаттандырмайды,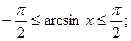

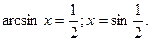
Жауабы: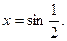

Мысалы, 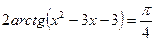теңдеуін шешейік.

Шешуі: Айнымалы енгіземіз: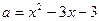

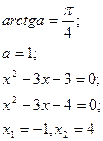
Жауабы: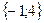

Мысалы, 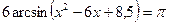теңдеуін шешейік.

Шешуі: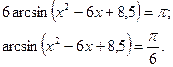

Айнымалы енгіземіз: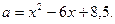

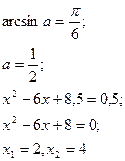
Жауабы: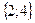

Мысалы, 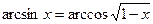теңдеуін шешейік.

Шешуі:

Айнымалы енгіземіз: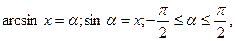

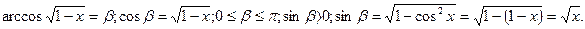
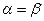-шарты бойынша, 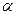және 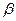- i ширектің бұрышы. Теңдеудің екі жағынан да синусты аламыз:

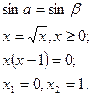
Тексереміз:

1) 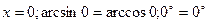-дұрыс

2) 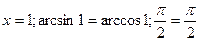-дұрыс

Жауабы: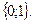

Мысалы, 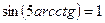теңдеуін шешейік.

Шешуі: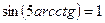

Айнымалы енгіземіз: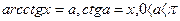

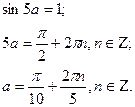
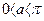болғандықтан, соңғы теңдікте n тек 0,1,2 мәндерін қабылдай алады. сонда мәнін тауып көрейік:

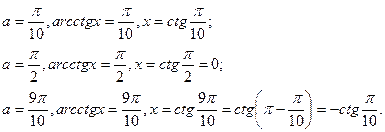
Жауабы: