Одномерные задачи фильтрации вязкопластичной жидкости
Движение аномальных нефтей в пластах по закону (7.5) 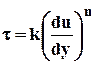 приводит к существенным особенностям разработки этих пластов, не встречающимся в случае фильтрации по закону Дарси.
приводит к существенным особенностям разработки этих пластов, не встречающимся в случае фильтрации по закону Дарси.
Установившееся течение. Рассмотрим плоскорадиальный приток несжимаемой вязкопластичной жидкости (ВПЖ) к скважине при условии выполнения соотношения (7.5), которое в этом случае принимает вид
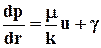 (u>0); (7.9)
(u>0); (7.9)
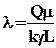 , (u=0).
, (u=0).
Выведем формулу для дебита скважины в круговом пласте, обобщающую формулу Дюпюи. Из (7.8) имеем:
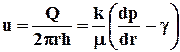 , если
, если 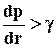 .
.
u=0, если dp/dr£g.(7.10)
Считая заданными постоянные давления на забое скважины и на границе пласта р(rc)=рc; р(Rк)=рк , после интегрирования (7.10) находим

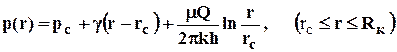 (7.11)
(7.11)
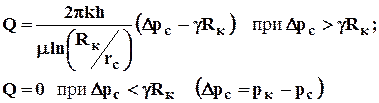 (7.12)
(7.12)
Формулами (7.11), (7.12) представлены, соответственно распределение давления в пласте и дебит скважины. Из формулы (7.11) видно, что часть разности давлений в виде линейного слагаемого с угловым коэффициентом g теряется на преодоление градиента давления сдвига. При Q®0, как следует из (7.11), давление не постоянно (как в случае фильтрации по закону Дарси), а изменяется по линейному закону. Как видно из (7.12), наличие предельного градиента давления в пласте ведет к уменьшению дебита скважины при тех же условиях по сравнению с фильтрацией по закону Дарси (формула Дюпюи). В рассматриваемом случае индикаторная линия скважины, т. е. зависимость Q(Dрс) - прямолинейная, но не проходит через начало координат, а отсекает на оси депрессий отрезок, равный gRк (рис. 7.3а).
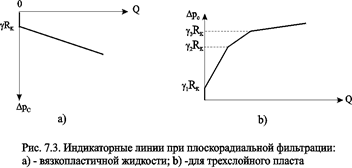
В случае слоистого пласта с гидродинамически изолированными пропластками, т. е. отсутствуют перетоки между слоями с разными проницаемостями, для дебита в каждом пропластке справедлива формула (7.12), но своими значениями толщин, проницаемости и начального градиента. Индикаторная линия в этом случае представляется ломаной, выпуклой к оси депрессии (рис. 7.3b).
Неустановившаяся фильтрация. Рассмотрим нестационарное течение упругой ВПЖ в упругой пористой среде. Дифференциальные уравнения для определения давления при упругом режиме пласта можно получить, дополняя закон фильтрации с предельным градиентом (7.5) или другую аппроксимацию нелинейного закона уравнением неразрывности и уравнением состояния флюида и пористой среды. Из данных соотношений получаем следующее уравнение пьезопроводности
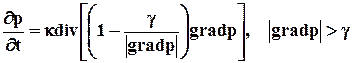 (7.13)
(7.13)
где k — коэффициент пьезопроводности.
Уравнение (7.13) служит основой для построения нелинейной теории упругого режима. При решении конкретных задач фильтрации для уравнения (7.13) формулируются обычные начальные и граничные условия, вытекающие из условий задачи. Вместе с тем следует иметь в виду, что при решении нестационарных задач на основе модели фильтрации с предельным градиентом в пласте образуется переменная область фильтрации, на границе которой (пока она не достигнет границы пласта) модуль градиента давления должен равняться предельному градиенту g, а давление - начальному пластовому.
Если рассмотреть задачу о пуске скважины с постоянным дебитом при фильтрации вязкопластичной жидкости с предельным градиентом, то получим из решения уравнения (7.13) следующую зависимость забойного давления от времени
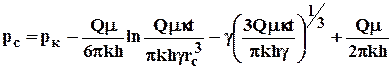 . (7.14)
. (7.14)
В данной формуле логарифмический член играет основную роль при малом времени, когда преобладают упругие силы. При больших значениях времени закон движения границы возмущенной области подчиняется степенному закону. Таким образом, при некоторых значениях параметров оказывается, что основное значение имеет степенной член, так что закон падения давления на забое скважины изменяется с логарифмического на степенной. Следовательно, при больших временах вид кривых изменения забойного давления рс(t) при фильтрации с предельным градиентом существенно изменяется по сравнению с фильтрацией упругой жидкости. В принципе это позволяет обнаружить в пластовых условиях проявление предельного градиента давления.
