Резисторы. Виды резисторов. Параллельные и последовательные соединения резисторов
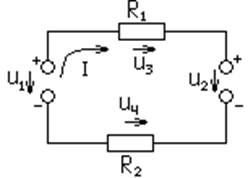
В электрических схемах необходимые сопротивления участков цепей создается с помощью специальных радиоэлементов, называемых резисторами. Они могут быть постоянными (рис1 а), подстроечными (рис1 б) или переменными (рис1 в) и имеют различные номиналы.
При последовательном соединении резисторов сопротивление увеличивается :
Rпосл=R1+R2+R3 (рис 1 д),
А при параллельном соединении общее сопротивление Rпар будет меньше наименьшего сопротивления и может быть определено по формуле:
1/Rпар=1/R1+1/R2+1/R3 (рис 1 г)
При параллельном соединении двух резисторов R1 и R2 получим :
Rпар= R1* R2/( R1+ R2) (1.6)
Рис. 1 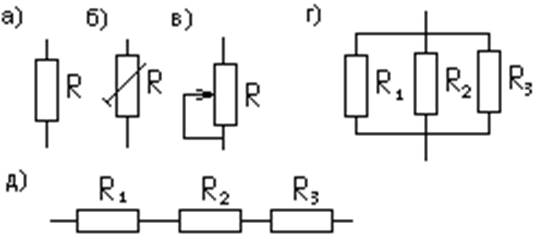
Закон Ома для участка и полной электрической цепи.
Как было отмечено в п. 1.5.1. сила тока в цепи при неизменном значении э.д.с. источника питания зависит от сопротивления этой цепи. Эта зависимость была установлена немецким ученым Георгом Омом в 1827г. И математически записывается в виде:
I=U/R (1.7)
Зависимость (1.7) называется "законом Ома для участка цепи"
Из формулы (1.7) следует другое определение единицы сопротивления. За единицу сопротивления 1 Ом принимают сопротивление такого проводника, по которому проходит ток 1А при напряжении на его концах 1 В.
Для цепи с последовательным соединением резисторов (рис 1 а) значение протекающего в ней тока равно:
I=U1/R1= U2/R2= U3/R3=U/(R1+R2+R3)
В цепи с параллельным включением резисторов токи, протекающие через эти резисторы, зависят от сопротивлений этих резисторов и на основании закона Ома определяются по формулам:
I1=U/R1; I2= U/R2; I3= U/R3
Общий ток Iобщ=I1+I2+I3
В отличие от э.д.с. или напряжения источника тока напряжение на сопротивлении участка цепи (резисторе) называют падением напряжения, подчеркивая этим, что сопротивления не создают напряжения, а на них лишь происходит распределение (падение) напряжения источника тока.
Любой источник питания характеризуется не только э.д.с., но и внутренним сопротивлением Ri. Поэтому если к такому источнику подключить нагрузку с сопротивлением Rh, то возникший в цепи ток будет протекать как через нагрузку , так и внутреннее сопротивление (рис 1). Следовательно закон Ома для неполной цепи имеет вид:
I=E/(Ri+Rh) (1.8)
E=I*Ri+I*Rh (1.9)
Формула (1.9) показывает, что э.д.с. источника равна сумме падений напряжении на внутреннем сопротивлении источника и на нагрузке. Чем больше Ri , тем больше напряжение на нем падает, а напряжение на нагрузке Uh уменьшается.
Рис. 1 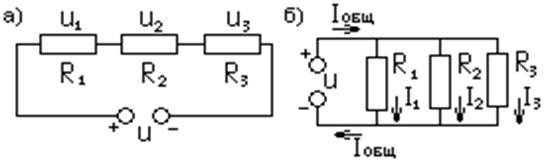
Рис. 2 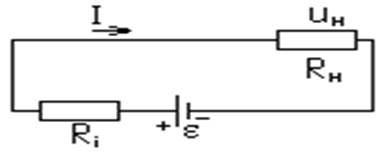
Законы Кирхгофа.
Первый закон Кирхгофа гласит, что сумма всех токов, протекающих через узел, равна нулю. Согласно этому закону применительно к узлу А (рис 1 а) можно записать:
I1+I2-I3=0 (1.10)
В этом уравнении токи I1 и I2, втекающие в узел, приняты положительными, а ток I3, вытекающий из узла, - отрицательным.
Первый закон Кирхгофа можно сформулировать иначе: сумма токов, втекающих в узел, равна сумме токов вытекающих из узла.
Согласно второму закону Кирхгофа сумма всех напряжений замкнутой цепи равна нулю.
Пусть дана электрическая цепь (рис 1 б), содержащая два источника U1 и U2 и резистор R1 и R2. Выберем произвольно направление общего тока I. Напряжения, направления которых совпадает с направлением тока I будем считать положительными, неудовлетворяющие этим требованиям - отрицательными. Тогда можно записать:
U3+U2-U4-U1=0
Рис. 1 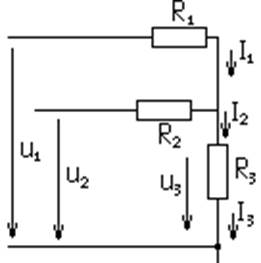
Рис. 2