Оценка параметров линейной регрессии и коэффициента корреляции
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида 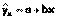 или
или 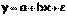 .
.
Уравнение вида 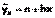 позволяет по заданным значениям фактора x находить теоретические значения результативного признака, подставляя в него фактические значения фактора x.
позволяет по заданным значениям фактора x находить теоретические значения результативного признака, подставляя в него фактические значения фактора x.
Построение линейной регрессии сводится к оценке ее параметров – a и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических 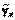 минимальна:
минимальна: 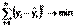
Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю.
Обозначим 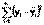 через S(a,b):
через S(a,b): 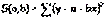 , тогда
, тогда
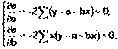
После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров a и b:
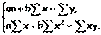
Решая систему уравнений, найдем искомые оценки параметров a и b:
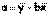 ,
, 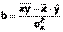 , где
, где 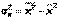 .
.
Так как 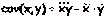 , то
, то 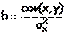
Параметр b называется коэффициентом регрессии. Он имеет смысл показателя силы связи между вариацией x и вариацией y. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Коэффициент a может не иметь экономического содержания, интерпретировать можно только знак, он показывает направления связи.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy, который можно рассчитать по следующим формулам:
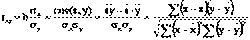
Линейный коэффициент корреляции находится в пределах: -1≤rxy≤1. Чем ближе он по модулю к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 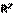 , называемый коэффициентом детерминации. Коэффициент детерминации показывает сколько процентов приходится на долю учтенных в модели факторов:
, называемый коэффициентом детерминации. Коэффициент детерминации показывает сколько процентов приходится на долю учтенных в модели факторов: 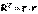
Соответственно величина 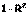 характеризует долю дисперсии y, вызванную влиянием остальных, не учтенных в модели, факторов.
характеризует долю дисперсии y, вызванную влиянием остальных, не учтенных в модели, факторов.
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка параметров уравнения регрессии осуществляется с помощью t-критерия Стьюдента. С этой целью по каждому из параметров определяется его стандартная ошибка: mb, ma и mr.
Стандартная ошибка коэффициента регрессии определяется по формуле:
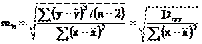
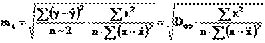
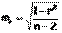
Величина стандартной ошибки совместно с t-распределением Стьюдента при n-2 степенях свободы применяется для проверки значимости коэффициента регрессии и для расчета его доверительного интервала.
Для оценки значимости коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента:
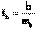 , причем
, причем 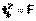
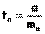
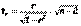 , причем
, причем 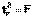 , т.е.
, т.е. 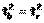
которое затем сравнивается с табличным значением при определенном уровне значимости a и числе степеней свободы n-2.
Если tфакт>tтабл, то делается вывод о значимости параметра.
