Коэффициент гидравлического сопротивления при течении в трубах
Для определения коэффициента гидравлического сопротивления при течении неньютоновских вязких жидкостей в трубах воспользуемся соображениями теории размерностей.
Рассмотрим жидкость с реологическим уравнением
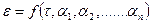 ,
,
где 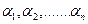 - реологические параметры.
- реологические параметры.
Можно утверждать, что перепад давления 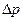 зависит от следующих определяющих параметров: длины
зависит от следующих определяющих параметров: длины 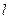 , диаметра
, диаметра 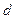 , плотности
, плотности 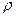 , средней скорости в сечении трубы
, средней скорости в сечении трубы 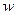 и реологических параметров жидкости [9].
и реологических параметров жидкости [9].
Таким образом
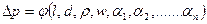 (3.27)
(3.27)
Приняв величины 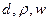 в качестве параметров с независимыми размерностями и учитывая, что
в качестве параметров с независимыми размерностями и учитывая, что 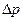 возрастает линейно при увеличении
возрастает линейно при увеличении 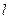 , из формулы (3.27) получим
, из формулы (3.27) получим
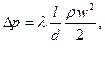
где
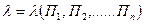 (3.28)
(3.28)
причем величины
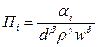
представляют собой критерии подобия.
Из формул (3.27) и (3.28) следует, что число критериев подобия равно числу реологических параметров жидкости.
Рассмотрим в качестве примера вязкопластичную жидкость (жидкость Бингама – Шведова). В этом случае формула (3.27) принимает вид
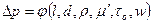 ,
,
а выражение (3.28)
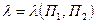 , (3.29)
, (3.29)
где
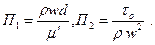
Для получения аналитического вида зависимости (3.29) для ламинарного течения рассмотрим формулу (3.21). Её можно представить в виде
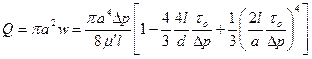 (3.40)
(3.40)
или
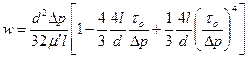 (3.41)
(3.41)
Положим
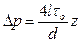 (3.42)
(3.42)
и подставим это выражение в формулу (3.41). Тогда после элементарных преобразований имеем [9]
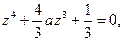 (3.43)
(3.43)
где
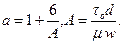 (3.44)
(3.44)
Используя стандартную методику решения уравнений четвертой степени, получим, что корни уравнения (3.43) равны
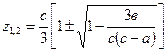 (3.45)
(3.45)
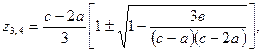 (3.46)
(3.46)
где
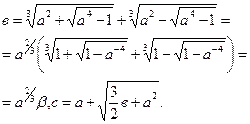 (3.47)
(3.47)
Рассмотрим подкоренное выражение в формуле (3.46). Так как в соответствии со вторым равенством (3.47)
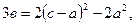 (3.48)
(3.48)
то после элементарных преобразований имеем
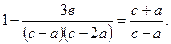
Поскольку в соответствии с формулой (3.44) а > 1, то из равенства (3.47) следует, что в и с величины вещественные, причем в > 0, с > а. Таким образом
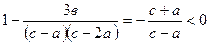
и корни 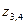 - комплексные.
- комплексные.
Перейдем к рассмотрению корней 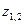 . Непосредственной проверкой можно убедиться, что
. Непосредственной проверкой можно убедиться, что
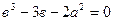 (3.49)
(3.49)
из формул (3.47) и (3.48) имеем
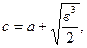 (3.50)
(3.50)
подставив это выражение в формулу (3.45), получим
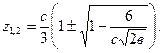 (3.51)
(3.51)
Из формул (3.47) следует, что при а = 1, в = 2, с = 3и
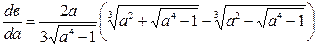
откуда 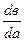 > 0 при а > 1. Таким образом функции в(а) и с(а) монотонно возрастают с ростом а и
> 0 при а > 1. Таким образом функции в(а) и с(а) монотонно возрастают с ростом а и 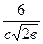 < 1.
< 1.
Итак, корни 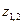 - вещественные. Для дальнейшего анализа перепишем, используя формулы (3.42), (3.43), (3.48), (3.50), соотношение (3.51) в виде
- вещественные. Для дальнейшего анализа перепишем, используя формулы (3.42), (3.43), (3.48), (3.50), соотношение (3.51) в виде
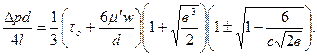 (3.52)
(3.52)
Переходя в равенстве (3.52) к пределу при 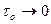 , получим
, получим
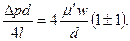
Этот предельный переход должен привести к формуле Пуазейля. Следовательно, в формулах (3.51) и (3.52) необходимо выбрать знак «плюс» и окончательно
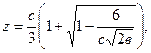
или с учетом равенства (3.42)
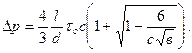 (3.53)
(3.53)
Как следует из формул (3.44) и (3.47), в = в(А), с = с(А). Сравнивая выражение (3.53) с формулой Дарси – Вейсбаха, получим
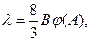
где 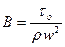 - безразмерный параметр,
- безразмерный параметр,
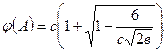
Таким образом коэффициент гидравлического сопротивления при течении жидкости Бингама – Шведова есть функция двух взаимно независимых критериев подобия А и В, причем В совпадает с 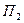 в формуле (3.29), а
в формуле (3.29), а
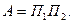
Численные значения функции 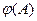 приведены в таблице. Можно показать, что при
приведены в таблице. Можно показать, что при 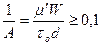 функция
функция 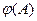 может быть аппроксимирована с погрешностью менее 2% выражением
может быть аппроксимирована с погрешностью менее 2% выражением
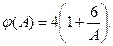
Таблица
| 1/А | 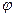 (А) (А) | 1/А | 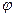 (А) (А) | 1/А | 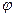 (А) (А) | 1/А | 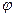 (А) (А) |
| 0,0000 | 3,00 | 0,0060 | 3,53 | 0,0250 | 4,25 | 0,0700 | 5,52 |
| 0,0005 | 3,14 | 0,0080 | 3,63 | 0,0300 | 4,40 | 0,0800 | 5,78 |
| 0,0010 | 3,20 | 0,0100 | 3,71 | 0,0350 | 4,55 | 0,1000 | 6,29 |
| 0,0020 | 3,29 | 0,0120 | 3,79 | 0,0400 | 4,70 | 0,1500 | 7,54 |
| 0,0030 | 3,36 | 0,0140 | 3,87 | 0,0450 | 4,84 | 0,2000 | 8,76 |
| 0,0040 | 3,42 | 0,1600 | 3,94 | 0,0500 | 4,98 | 0,2500 | 9,97 |
| 0,0050 | 3,48 | 0,0200 | 4,08 | 0,0600 | 5,25 | 0,3000 | 1 1,18 |
В качестве следующего примера рассмотрим степенную жидкость. Для этой жидкости формула (3.27) принимает вид
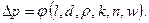
Приняв в качестве параметров с независимыми размерностями величины 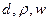 , используя
, используя 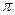 -теорему и учитывая, что
-теорему и учитывая, что 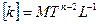 , получим
, получим
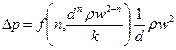
откуда
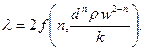
Безразмерными критериями подобия являются величины
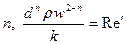
где 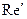 - аналог числа Рейнольдса для вязкой жидкости.
- аналог числа Рейнольдса для вязкой жидкости.
Для выяснения вида зависимости 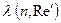 рассмотрим выражение, следующее из формулы (3.26)
рассмотрим выражение, следующее из формулы (3.26)
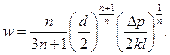 (3.54)
(3.54)
Разрешив соотношение (3.54) относительно 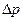 , получим
, получим
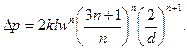
Сравнивая это выражение с формулой Дарси – Вейсбаха, имеем
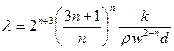 .
.
