Теплоотдача без изменения агрегатного состояния теплоносителя

Свободное движение (естественная конвекция). Свободное движение жидкости (газа) целиком определяется теплообменом. Чем интенсивнее теплообмен, тем интенсивнее движение. В свою очередь, количество передаваемого тепла пропорционально поверхности тела и разности температур поверхности и жидкости или газа. В результате свободное движение теплоносителя в конечном счете определяется этими факторами. Температурным напором определяется разность плотностей и подъемная сила, а поверхностью – зона распространения процесса. При этом играет роль как размер поверхности, так и ее ориентация в пространстве. Так, при теплообмене между жидкостью или газом и обтекаемой или вертикальной поверхностью разность температур по сечению потока вверху и внизу, а следовательно скорость и режим движения зависят от высоты стенки. При теплообмене с горизонтальной поверхностью гидродинамическая обстановка определяется направлением теплового потока и расположением источника теплоты по отношению к жидкости (газу). Если жидкость или газ находятся над горизонтальной поверхностью, то естественная конвекция возникает лишь при направлении теплового потока от стенки к жидкости. При охлаждении жидкости аналогичная картина имеет место, когда тепловой поток направлен сверху вниз (например, при охлаждении воды в водоемах). При расположении греющей поверхности над жидкостью характер течения будет иным. Однако во всех случаях при горизонтальном расположении поверхности теплообмена характер течения зависит от ее наименьшего размера, который принимается за определяющий. Например, для горизонтальных труб определяющим размером является диаметр. С учетом влияния направления теплового потока (от стенки к теплоносителю или от теплоносителя к стенке) введением множителя (Pr_ж/Pr_ст)^0,25 критериальное уравнение конвективного теплообмена при свободном движении представляют в виде

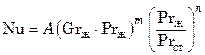. (7.85)

Явный вид уравнения (7.85) для некоторых наиболее распространенных случаев на практике приведен ниже.

Для горизонтальных труб при 10³ < Gr∙Pr < 10⁹:

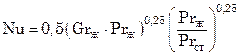. (7.86)

Для вертикальных труб и пластин:

при 10³ < Gr_ж∙Pr_ж< 10⁹

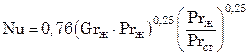; (7.87)

при Gr_ж∙Pr_ж> 10⁹

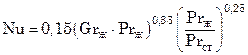. (7.88)

Для горизонтальных пластин, обращенных нагретой поверхностью вверх:

при Gr_ж∙Pr_ж = 2∙10⁷÷3∙10¹⁰

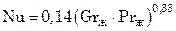; (7.89)

при Gr_ж∙Pr_ж = 10⁵÷2∙10⁷

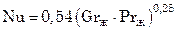. (7.90)

Для горизонтальных пластин, обращенных нагретой поверхностью вниз при Gr_ж∙Pr_ж = 3∙10⁵÷3∙10¹⁰

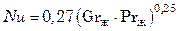. (7.91)

В качестве определяющего геометрического размера в уравнениях (7,86÷7,91) приняты для горизонтальных труб диаметр d, а для вертикальных поверхностей их высота h. Определяющей температурой принята температура жидкости (газа) в ядре потока.

Для неньютоновских жидкостей, подчиняющихся степенному закону :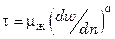

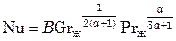, (7.92)

где .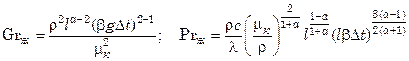

Уравнение (7.92) справедливо при Pr_ж > 10. Величина коэффициента B зависит от значения a, формы и пространственной ориентации поверхности теплообмена (табл. 7.2).

Таблица 7.2 – Значения коэффициента B в уравнении (7.92)

Форма поверхности	lопр	a = 0,1	a = 0,5	a = 1,0	a = 1,5
Вертикальная труба или плита высотой h	h	0,60	0,63	0,67	0,71
Горизонтальная труба радиуса R	R	0,36	0,38	0,42	0,45

В узких каналах и щелях из-за ограниченного пространства и наличия восходящих и нисходящих потоков условия свободного движения значительно отличаются от свободного движения в неограниченном пространстве. В этих случаях средняя плотность теплового потока рассчитывается по формулам теплопроводности, где коэффициент теплопроводности среды заменяется эквивалентным коэффициентом теплопроводности, который учитывает перенос теплоты путем как теплопроводности, так и конвекции: .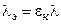

Если Gr_ж∙Pr_ж≤ 10³, 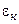принимается равным единице 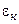= 1. В области Gr_ж∙Pr_ж > 10³

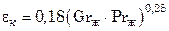. (7.93)

В качестве определяющего линейного размера в этом случае принимают толщину прослойки жидкости (газа), определяющей температуры – температуру жидкости .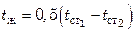

Вынужденное движение. Интенсивность теплоотдачи при вынужденном движении зависит в первую очередь от характера движения жидкости (газа), а также от тепловой стабилизации потока. При вынужденном движении теплоотдача по длине трубы неодинакова. Непосредственно у входа коэффициент теплоотдачи имеет максимальное значение, на последующих участках длины он резко убывает, стремясь к некоторому предельному значению, которое затем остается неизменным. Длина участка тепловой стабилизации зависит от теплопроводности жидкости (газа), диаметра трубы, ее положения в пространстве, наличия и направления естественной конвекции, наличия гидродинамической стабилизации. При горизонтальном положении трубы для среднего по длине коэффициента теплоотдачи длина участка тепловой стабилизации l_c = 50d. Поэтому для коротких труб (l_c/d < 50) при расчете коэффициента теплоотдачи вводится поправка ε_l, учитывающая влияние стабилизационного участка на величину α_ср.

При ламинарномрежиме движения теплоносителя по трубам и каналам происходит значительное изменение температуры по сечению потока. Вследствие этого на вынужденное движение теплоносителя накладывается свободное движение, интенсивность которого характеризуется критерием Грасгофа. С учетом влияния свободной конвекции критериальное уравнение конвективного теплообмена для этого случая:

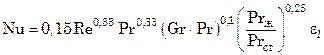. (7.94)

Определяющим размером в уравнении (7.94) является диаметр трубы или эквивалентный диаметр канала любой формы, а определяющей температурой – средняя температура потока. Коэффициент ε_l, зависящий от отношения l/d, для коротких труб может быть определен из ряда:

l/d
εl	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1,0

Для неньютоновских жидкостей, подчиняющихся указанному закону,

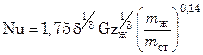, (7.95)

где .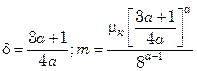

При турбулентномрежиме движения теплоносителя по прямым трубам и каналам в результате интенсивного перемешивания естественная конвекция практически не оказывает влияния на интенсивность теплообмена. Для определения среднего по длине канала или трубы коэффициента теплоотдачи рекомендуется уравнение

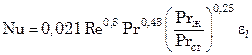. (7.96)

Для газов это уравнение упрощается:

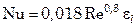. (7.97)

В качестве определяющего размера здесь принят диаметр трубы или эквивалентный диаметр, определяющей температуры – средняя температура потока. При l/d ≥ 50 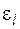= 1. Значения 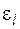для труб с l/d < 50 приведены в табл. 7.3.

Таблица 7.3 – Значения 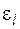для труб с l/d < 50 при Re ≥ 10⁴

l/d Re
1·104	1,65	1,5	1,34	1,23	1,13	1,07	1,03
2·104	1,51	1,4	1,27	1,18	1,10	1,05	1,02
5·104	1,34	1,27	1,18	1,13	1,08	1,04	1,02
1·105	1,28	1,22	1,15	1,10	1,06	1,03	1,02
1·106	1,14	1,11	1,08	1,05	1,02	1,02	1,01

Уравнение теплоотдачи для турбулентного потока неньютоновских жидкостей, подчиняющихся степенному закону:

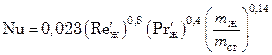, (7.98)

где .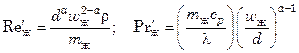

При течении жидкости в изогнутых трубах – змеевиках – коэффициент теплоотдачи увеличивается вследствие возникновения под влиянием центробежного эффекта вторичной циркуляции жидкости. Расчет теплоотдачи в таких случаях производится по уравнениям для прямых труб, но вводится поправка в виде коэффициента ε_R = 1 + 1,77(d/R), где d – диаметр трубы; R – радиус змеевика. Таким образом,

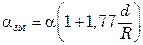. (7.99)

Теплоотдача при переходном(неустойчиво турбулентном) режиме, соответствующем значениям критерия Рейнольдса 2300<Re_ж<10⁴, приближенно может быть рассчитана по уравнению

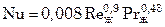(7.100)

либо при помощи функции

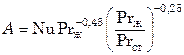, (7.101)

значения которой для различных чисел Re приведены ниже:

Re 10–3	2,3	2,5		3,5
A	3,6	4,9	7,5		12,2	16,5

При механическом перемешивании жидкостей величина коэффициента теплоотдачи зависит от типа теплообменного устройства (рубашка, змеевик и т.д.), наличия отражательных перегородок, конструкции мешалки и физических свойств перемешиваемой среды.

Уравнение конвективного теплообмена в аппаратах с лопастными и турбинными мешалками и наружными рубашками при d/D = 1/3 и h = (0,2÷0,5)d

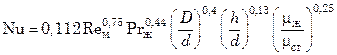, (7.102)

где d и h – диаметр и высота мешалки; D – диаметр аппарата; 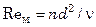(n – число оборотов мешалки в минуту).

В аппаратах с погружными змеевиками при прочих равных условиях коэффициент теплоотдачи возрастает в 1,5–2 раза.

Наибольшей интенсивностью теплоотдачи отличаются аппараты с лопастными (листовыми) мешалками, имеющими размеры: d = D и h = 0,5H (H – уровень жидкости в аппарате). В случае наружной тепловой рубашки

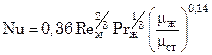, (7.103)

а в аппаратах с погружным змеевиком

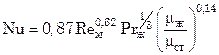. (7.104)

Для аппаратов с рубашками, снабженных пропеллерными мешалками, коэффициент теплоотдачи определяют из уравнения

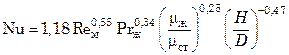. (7.105)

В аппаратах с турбинными мешалками при наличии змеевика:

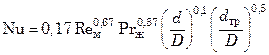, (7.106)

где d_тр – наружный диаметр трубы змеевика.