Кирхгофтың екінші заңы бойынша 6 страница

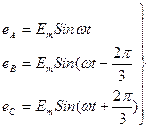
Техникалы және үнемділі артықшылықтары үшфазалы токқа бүгінгі электротехникада бастаушы орынды қамтамасыз етеді.

6.2 Жұлдызша және үшбұрышты жалғанған электр тізбектер

Фазалық ораманың екі шықпасы бар, оларды ораманың басы және аяғы деп атайды.

6.2-суреттегі сүлбеде үшфазалы генератордың орамаларының қосылуы жұлдызша деп аталады; генератордың фазалық орандарының аяғы бір ортақ нүктеде қосылған. Келесіде жұлдызша қосылуды 6.5-суреттегідей көрсетеміз. Генератордың фазалық орамдарының ортақ нүктесі бейтарап нүкте деп аталады. Талаптарға қарай бейтарап нүкте N бөлек шықпаға шығарылады.

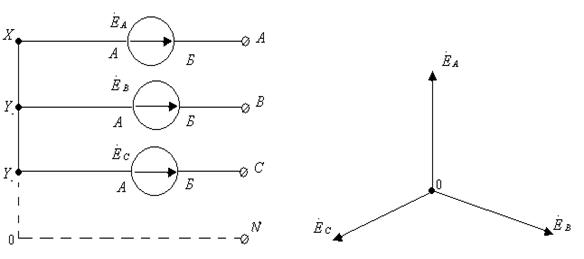
6.5-сурет. Үшфазалы генератордың жұлдызша қосылуы.

Генератордың орамаларын үшбұрышты қосқан кезде бір фазаның басын екінші фазаның аяғымен, екінші фазаның басын үшінші фазаның аяғымен, үшінші фазаның басын бірінші фазаның аяғымен қосады (6.6-сурет).

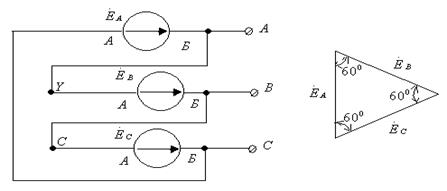
6.6-сурет. Үшфазалы генераторды үшбұрышты қосу.

Үш орама тұйықталған үшбұрышты құрады, ал ЭҚК-тердің қосындысы нөлге тең. Генератордың қосылған орамалардың ортақ нүктелерін сызықты сымдарға немесе жүктемеге қосады. Үшфазалы тізбекте жүктемеде немесе үшбұрышты немесе жұлдызша қосылуы мүмкін.

6.3 Үшфазалы тізбекті симметриялық ережесі

Үшфазалы тізбекті және үшфазалы қабылдағышты егер де барлық фазалардың комплекстік кедергілері бірдей болса симметриялық деп атайды, ал болмаса – симметриялық емес ереже дейді.

6.8-суретте симметриялық ереже кезде 6.7-суретте көрсетілген сүлбе үшін және жүктеме индуктивтік түрде болғанда топографикалық және токтардың диаграммалары келтірілген.

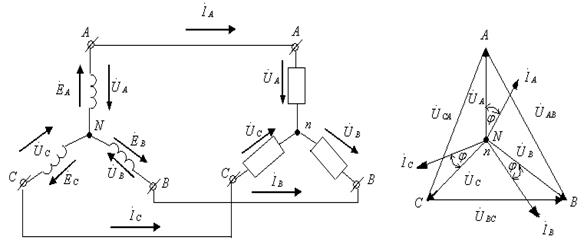
6.7-сурет. Генератор және қабылдағыш 6.8-сурет. Топографика-

жұлдызша қосылған сүлбе. лық және токтар

диаграммалар.

Сызықтық кернеулер фазалық кернеулердің айырымдарына тең:

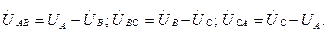(6.2)

Тең бүірлі үшбұрыш ANB-ден шығады:

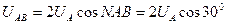немесе 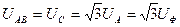(6.3)

6.10 суретте симметриялық ереже кезде 6.9-суретте көрсетілген сүлбе үшін және 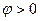болған кезде топографикалық және токтарды диаграммасы келтірілген.

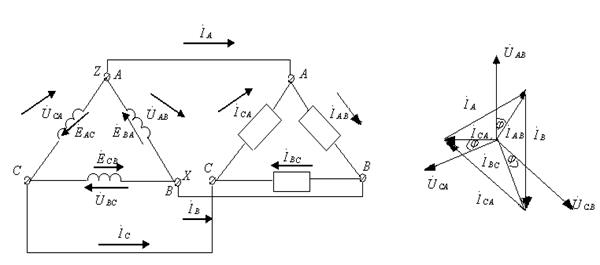
6.9-сурет. Генератор және қабылдағыш 6.10-сурет. Топографи-

үшбұрышты қосылған сүлбе. калық және токтар

диаграммалар.

Сызықты токтар фазалық токтардың айырымдарына тең:

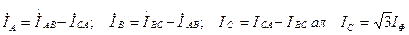(6.4)

Симметриялық үшфазалы қабылдағыштың активтік қуаты тең:

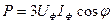(6.5)

Қабылдағыштың тармақтарын жұлдызша қосқанда 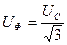және 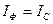, ал қабылдағыштың тармақтарын үшбұрышты қосқанда 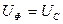және 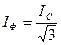болатынын есекке алғанда қосудың түріне тәуелсіз шығады:

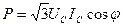(6.6)

Бұл кейіптемедегі 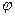-фазалық кернеумен фазалық токтың арасындағы бұрыш (фазалық ығысу).

Үйлесті реактивтік және толық қуаттар үшфазалы қабылдағыш үшін:

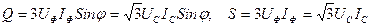(6.7)

Симметриялық тізбекте (6.11-сурет) токтарды симметриялық ережеде есептеу тәртібін қарайық.

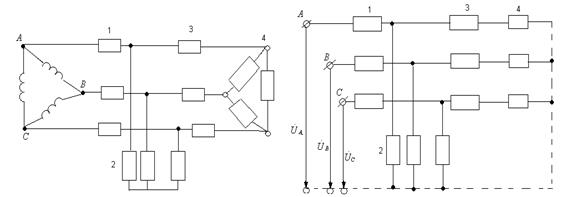
а) б)

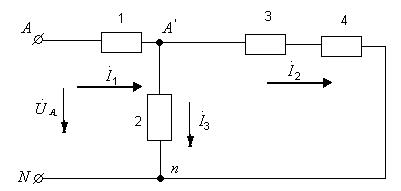
в)

6.11-сурет. Берілген симметриялы тізбек (а), түрлеген симметриялық тізбек (б), бірфазалы есептеу тізбек (в).

Көркендіру көздің кернеу және 1,2,3,4 тізбектің элементтерінің кедергілері берілген. Есептеуді өткізу үшін көріктендіру көздің және 4 элементтерінің үшбұрыштан жұлдызшаға алмастыру керек. Симметриялық жұлдыздың фазалық кедергілер баламалы симметриялық үшбұрыштың кедергілерінен 3 есе аз. Баламалы көріктендіру көздің фазалық кернеулері берілген сызықтық кернеулерден 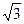есе аз.

Сонымен, 6.11, б-суретте көрсетілген сүлбеге келеміз. Симметриялық ережеде бейтарап нүктелердің потенциалдары бірдей. Сондықтан, сүлбенің ережесін бұзбай оларды кедергісі жоқ сыммен бір бірімен қосамыз (үзік-үзік сызық). Содан кейін сүлбеден екі фазаны шығарып тастап 6.11,в-суреттегі сүлбеге келеміз. Бұл жағдай қалған А фазаның ережесін өзгертпейді.

Бірфазалы сүлбедегі токтар жеңіл табылады. В және С фазадағы токтар модуль бойынша А фазадағы токтарға тең, ал аргумент бойынша бұрышқа қалады және озады. Үшбұрыштың тармақтарындағы ток элемент 3 өткен токтан 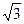есе аз.

6.4 Үшфазалық тізбектің симметриясыз ережесі

Үшфазалы тізбекте симметриясыздық бірнеше себептен болуы мүмкін:

- фазалардың кедергілерінің тең болмаумен (симметриясыз жүктеме); - симметриясыз қысқа тұйықталумен (мысалы, екі фаза арасында);

- фазаның ажыратылумен;

- ЭҚК-тердің айырмашылығымен және т.б.с.

1.Бейтарап сымы бар жұлдызша қосылған симметриясыз үшфазалы тізбек 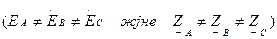. 6.12-суретте көрсетілген симметриясыз үшфазалы тізбектің екі түйіні болғандықтан түйінді потенциалдар әдісін қолданамыз.

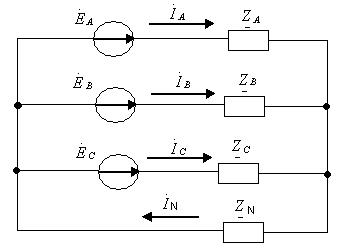
6.12-сурет. Бейтарап сымы бар жұлдызша қосылған симметриясыз үшфазалы тізбек

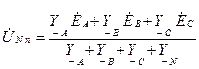(6.18)

мұнда 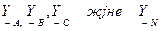-сәйкесті тармақтардың өткізгіштіктері.

Содан кейін тармақтардағы Ом заңы бойынша токтарды табамыз:

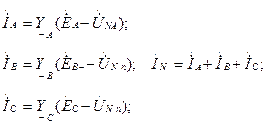
Егер де фаза немесе бейтарап сым ажаратылса, онда сол фазаның немесе бейтарап сымның өткізгіштігі нөлге тең болады.

Мысалы, бейтарап сым жоқ кезде 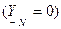шығады:

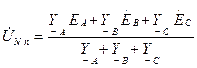(6.10)

2. Шықпаларында берілген сызықты кернеулері бар жұлдызша қосылған симметриясыз үшфазалы жүктеу (6.13-сурет).

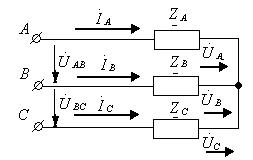
6.13-сурет

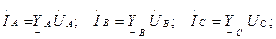
Кирхгофтың бірінші заңы бойынша:

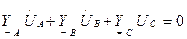(6.11)

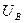және 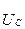фазалық кернеулер 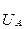және берілген сызықты кернеулер арқылы мынаған тең:

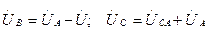(6.12)

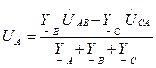(6.13)

Сол сияқты 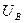және 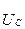фазалық кернеулер үшін:

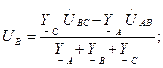
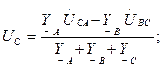(6.14)

3. Шықпаларында берілген кернеулері бар үшбұрышты қосылған симметриясыз үшфазалы жүктеме (6.14-сурет).

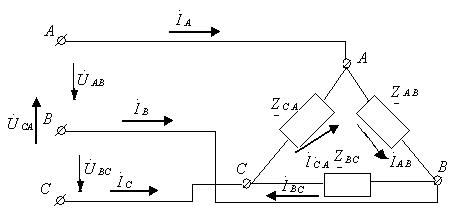
6.14-сурет. Үшбұрышты қосылған симметриясыз үшфазалы жүктеме.

Жүктеменің кедергілендегі токтар тең:

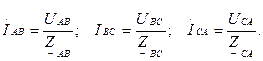
Сызықтағы токтар жүктеменің сәйкесті токтарының айырымы ретінде табылады: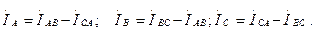

6.5 Симметриясыз үшфазалы тізбектің қуаты

Үшфазалы тізбектің толық қуаты комплексті түрде тең:

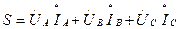(6.15)

Бұл теңдеудің нақтылы бөлігі активтік қуат болады:

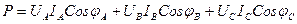(6.16)

Симметриясыз үшфазалы тізбектің тұтынытын қосынды активтік үш ваттметрлердің көмегімен өлшеуге болады. Ваттметрлердің кернеу орауыштары фазалық кернеулерге қосылады, ал ток орауыштар сол сәйкесті фазаларға тізбектеп қосылады (6.15-сурет). Активтік қуат үш ваттмердің қосында көрсетуіне тең, яғни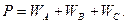

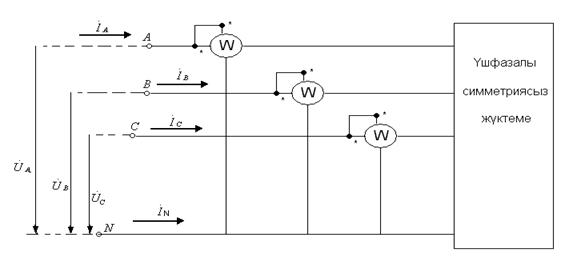
6.15-сурет. Бейтарап сым бар кезде қуатты өлшеу.

Егер де бейтарап сым жоқ болса, онда қуатты екі ваттметр көмегімен өлшеуге болады.

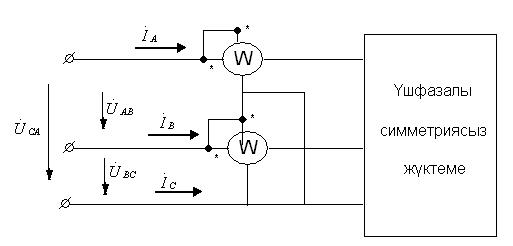
6.16-сурет. Қуатты екі ваттметрмен өлшеу.

Бұл жағдайда (6.15) көрініс келесі түрде түрлендіріледі: ток 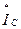мынаған тең деп алып 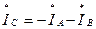табамыз:

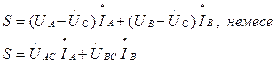(6.17)

(6.17) көрініп тұр: қуатты екі ваттметрмен өлшеген кезде бір ваттметірдің кернеу орауышы 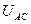сызықты кернеуге қосылады, ал ток орауышы А фазаға тізбектеп қосылады, екінші ваттметрдің кернеу орауышы 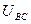сызықты кернеуге қосылады, ал ток орауышы В фазаға тізбектеп қосылады, сондықтан .

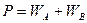Жетінші тарау