Т.4. Резонанс в электрических цепях

Определение резонанса

В электрической цепи, содержащей катушки индуктивности L и конден­саторы C, воз­можны свободные гармонические колебания энергии между маг­нитным полем катушки 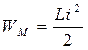и электрическим полем конденсатора 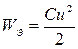. Угловая частота этих колебаний w_o, называемых свободными или собствен­ными, определяется структурой цепи и парамет­рами ее отдельных элементов R, L ,C.

Резонансным режимом цепи или просто резонансом называется явление увеличения амплитуды гармонических колебаний энергии в цепи, наблюдаемое при совпадении частоты собственных колебаний w_o с частотой вынужденных колебаний w, сообщаемых цепи источ­ником энергии (w_o = w).

В резонансном режиме колебания энергии между магнитным и электри­ческим по­лями замыкаются внутри цепи, обмен энергией между источником и цепью отсутствует, а вся по­ступающая от источника энергия преобразуется в другие виды, т.е. электрическая цепь по отношению к источнику энергии ведет себя как чисто активное сопротивление R (активная проводимость G). На этом основании условие для резонансного режима можно сформулиро­вать через па­раметры элементов схемы, а именно: входное сопротивление и, соответственно, входная проводимость схемы со стороны выводов источника энергии должна носить чисто активный характер: Z_вх=R_вх; Y_вх=G_вх; X_вх=0; B_вх=0; или в комплекс­ной форме: Im[Z_вх]=0, Im[Y_вх]=0.

Резонанс напряжений

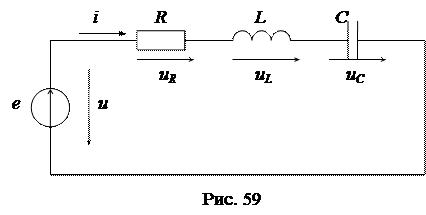
Резонанс в цепи с последовательным соединением источника энергии и реактивных элементов L и C получил название резонанса напряжений. Про­стейшая схема такой цепи по­казана на рис. 59.

Комплексное входное сопротивление схемы: .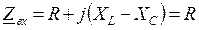

Условие резонанса напряжений: X_э= X_L - X_C или wL = 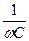, откуда w₀ = 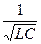- ре­зонансная или собственная частота.

Из полученного равенства следует, что резонансного режима в цепи можно достичь изменением параметров элементов L и C или частоты источника w.

В резонансном режиме полное сопротивление схемы имеет минимальное значение и равно активному сопротивлению:

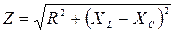= R,

а ток максимален и совпадает по фазе с напряжением источника: I=E/R; j = 0.

Векторная диаграмма напряжений и тока показана на рис. 60.

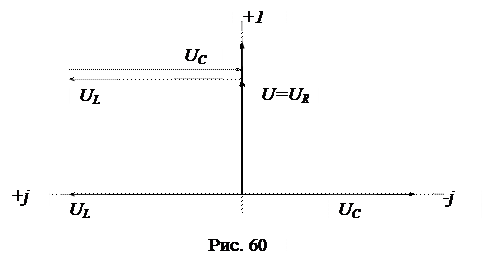Напряжения на реактивных элементах равны по модулю, противопо­ложны по фазе и взаимно компенсируют друг друга:

; ,

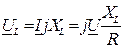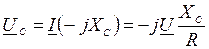а напряжение на резисторе равно напряжению источника : U_R=IR=U=E.

Равные по модулю напряжения на реактивных элементах U_L=U_C = 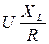могут зна­чи­тельно превосходить напряжение источника U = Е при условии, что X_L=X_C>>R.

Выясним энергетические процессы, протекающие в цепи в резонансном режиме. Пусть в цепи протекает ток i =I_msinwt, тогда напряжение на конденса­торе составит:

.

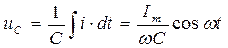Сумма энергий магнитного и электрического полей равна:

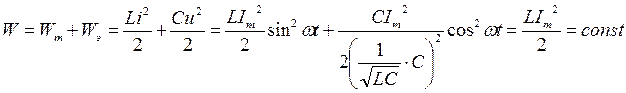
Таким образом, сумма энергий магнитного и электрического полей равна постоян­ному значению. Это значит, что между магнитным и электрическим по­лями происходит не­прерыв­ный обмен энергией, суммарное значение которой постоянно, а обмен энергией ме­жду ис­точником и цепью отсутствует, при этом поступающая от источника энергия преобра­зуется в другие виды..

Электрическая цепь с последовательным соединением элементов R, L, C в технике по­лучила название последовательного колебательного контура. Свой­ства такой цепи как ко­ле­бательного контура характеризуют следующие пара­метры: 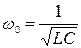- резонансная частота; r = 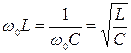- волновое со­противле­ние; Q = 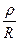- добротность.

Чем больше добротность контура Q, тем выразительнее проявляются в нем резо­нанс­ные явления; например, напряжения на реактивных элементах больше напряжения ис­точника в Q раз: U_L = U_C = UQ.

При изменении частоты источника w = var будут изменяться сопротивле­ния реак­тив­ных элементов и, как следствие, будут изменяться ток в цепи и на­пряжения на отдельных участках.

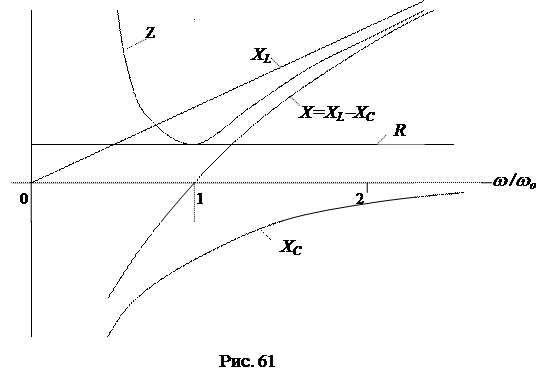
Частотными характеристиками контура называются зависимости сопро­тивлений от­дельных элементов и участков от частоты X_L =wL; X_C = 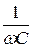; X =X_L-X_C ; Z= 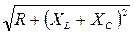(рис. 61).

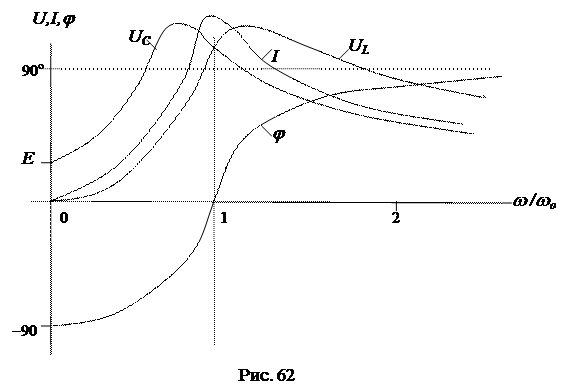
Резонансными характеристиками называются зависимости режимных па­раметров от частоты: U_L, U_C, I, j = f(w)(рис. 62).

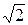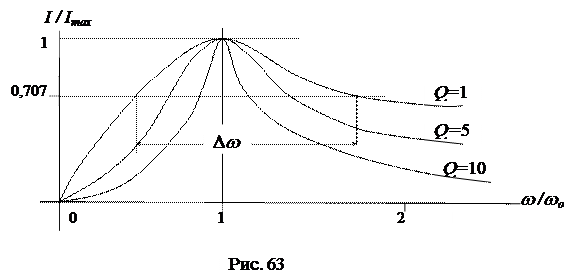
Полосой пропускания резонансного контура называют область частот Dw = w₁-w₂, на границах которой ток I в раз меньше своего максимального значения, т.е^. I=0,707I_max. Полоса пропускания контура обратно пропорцио­нальна его добротности: Dw = 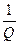. На рис. 63 в относительных единицах пред­ставлено семейство резонансных характеристик с различ­ными значениями доб­ротности.

Резонанс токов

Резонанс в цепи с параллельным соединением источника энергии и ре­активных эле­ментов L и C получил название резонанса токов. Простейшая схема такой цепи показана на рис. 64.

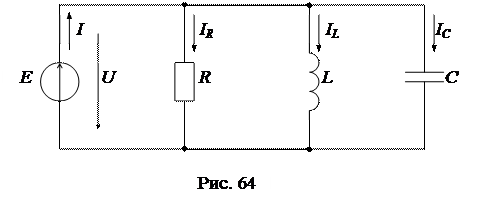
Комплексная входная проводимость схемы:

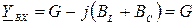
Условие резонанса токов: 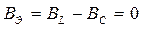или 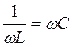, откуда 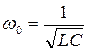- резо­нансная (собственная) частота.

Из полученного равенства следует, что резонансного режима в цепи можно достичь изменением параметров элементов L и C или частоты источ­ника w.

В резонансном режиме полная проводимость схемы равна активной про­водимости и имеет минимальное значение: 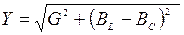= G, а ток ис­точника также минима­лен и совпадает по фазе с напряжением источника ( j = 0): I =UY = UG.

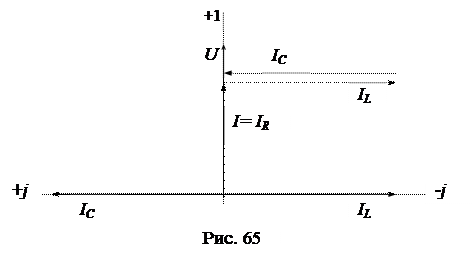
Токи в ветвях с реактивными элементами I_L=U(-jB_L), I_C =U(jB_C) равны по модулю, противоположны по фазе и компенсируют друг друга, а ток в рези­сторе G равен току источ­ника (I=I_G=UG). Равные по модулю токи в реактивных элементах I_L = I_C могут значительно превосходить ток источника I при усло­вии, что B_L=B_C>>G .

Векторная диаграмма токов и напряжений показана на рис. 65.

Электрическая цепь с параллельным соединением элементов G, L и C в технике по­лу­чила название параллельного колебательного контура. Свойства такой цепи как колеба­тель­ного контура характеризуют следующие параметры: 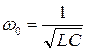- резонансная частота; 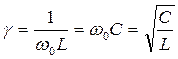- волновая проводи­мость; 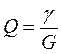- добротность.

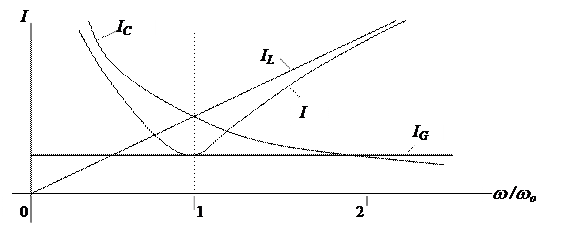
Резонансные характеристики параллельного контура представлены на рис. 66.

		Рис. 66

Резонанс в сложных схемах

Схемы замещения реальных электрических цепей могут существенно от­личаться от рассмотренных выше простейших последовательной или парал­лельной схем. Хотя условие резонансного режима в общем виде [ Im(Z_вх)=0 и Im(Y_вх)=0 ] для любой схемы сохраняется, однако конкретное содержание этих уравнений будет определяться структурой схемы заме­щения.

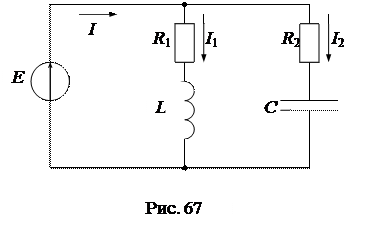
На рис. 67 приведена эквивалентная схема параллельного контура, в ко­то­рой ре­альные элементы цепи (катушка и конденсатор) представлены последо­вательными схемами замеще­ния.

Входная комплексная проводимость схемы:

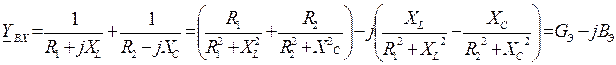
Условие резонанса:

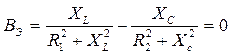или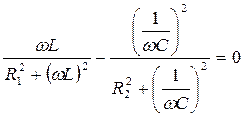

Отличие данного условия резонанса от аналогичного условия для про­стейшей схемы рис. 64 состоит в том, что в этом уравнении присутствуют пара­метры активных элементов R₁ и R₂.

Анализ полученного уравнения показывает, что при изменении парамет­ров одного из элементов схемы возможны различные варианты решения.

При изменении сопротивлений R₁ и R₂ возможны два варианта решения: 1)существует одна точка резонанса (корни уравнения вещественные; один по­ложительный, а другой отрицательный); 2)резонанс в схеме невозможен (корни уравнения комплексные).

При изменении индуктивности L или емкости C возможны три варианта решения: 1)существует две точки резонанса (корни уравнения вещественные и оба положительные); 2)существует одна точка резонанса (корни уравнения рав­ные и положительные); 3)резонанс в схеме невозможен (корни уравнения ком­плексные).

Решая уравнение резонанса относительно частоты, получим:

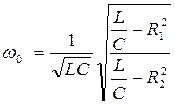
Анализ этого уравнения показывает, что при R₁ = R₂ резонансная частота имеет вы­ражение 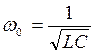, как и для простейшей схемы рис. 1, а при 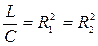для w₀ получа­ется неопределенное решение, что физически озна­чает резонансный режим на любой частоте.

На рис.10 приведена схема последовательного контура, в которой реаль­ные эле­менты (катушка и конденсатор) представлены различными схемами за­мещения.

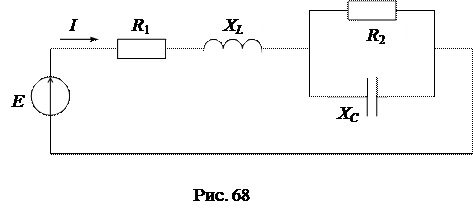Входное комплексное сопротивление схемы:

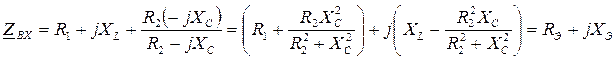
Условие резонанса:

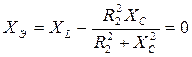или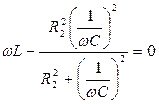

Анализ этого уравнения показывает неоднозначную зависимость условия резонанса от значений параметров каждого элемента схемы.

Если сложная схема содержит в своей структуре несколько (более двух) разнород­ных реактивных элементов, то при изменении частоты в ней могут наблюдаться несколько ре­зонансных режимов (как тока, так и напряжения) в зависимости от структуры схемы.