Построение классической линейной регрессии

Для построения линейной регрессии (парной и множественной), а также для оценки параметров линейных и нелинейных трендов в пакете STATISTICA 6.0 используется модуль Multiple Regression (Множественная регрессия).

Проведем построение уравнения регрессии зависимости фондоотдачи от среднечасовой производительности труда и удельного веса активной части ОПФ (приложение Е).

Шаг 1. В главном меню выберем: Statistics®Multiple Regression (Статистика® Множественная регрессия).

Рисунок 3.4 – Окно Multiple Linear Regression (Множественная линейная регрессия)

Шаг 2.В активном окне инициируем кнопку Variables (Переменные) и укажем зависимую и не зависимую переменную. В качестве зависимой переменной (Dependent var.) необходимо указать производительность труда – Y, в качестве не зависимых переменных (Independent var.) будут выступать X1 и X2.

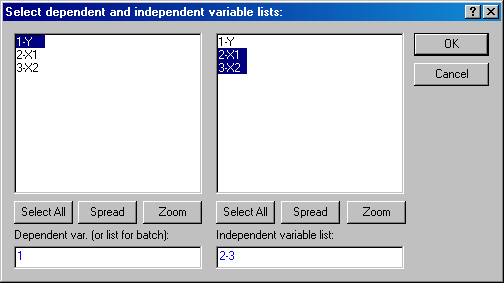
Рисунок 3.5 – Окно выбора зависимой и не зависимой переменных

Шаг 3. Выбираем опцию Review descriptive statistics, correlation matrix (Описательные статистик и матрица корреляции) и нажмем кнопку ОК.

Шаг 4. В появившемся окне Review Descriptive Statistic необходимо выбрать вкладку Advanced.

Рисунок 3.6 – Окно установок описательных статистик и корреляции

После чего становятся доступными следующие таблицы: Means & Standard Deviation (Средняя и стандартное отклонение), Correlations (Корреляция), Covariances (Ковариация), Box & whisker plot ( ), Matrix plot of correlations (Матрица диаграмм рассеяния).

Шаг 5. Выберем кнопку Correlations, в результате получим матрицу, содержащую значения парных коэффициентов корреляции (таблица 3.2).

Значения, представленные таблице показывают, что фактор X2 оказывает сильное положительное влияние на зависимую переменную Y (т.к. значение на пересечении соответствующего столбца и строки равно 0,868), фактор X1 оказывает слабое отрицательное влияние. Между переменными Х1 и Х2 связь практически отсутствует (значение коэффициента корреляции -0,117 близко к нулю).

Таблица 3.2 - Матрица парных коэффициентов корреляции

	X1	X2	Y
X1	1,000	-0,117	-0,351
X2	-0,117	1,000	0,868
Y	-0,351	0,868	1,000

Также можно представить полученные результаты в графическом виде, для этого выбираем кнопку Matrix plot of correlations (рисунок 3.6), полученный результат представлен на рисунке 3.7.

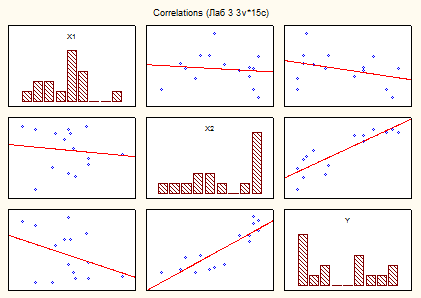
Рисунок 3.7 - Матрица диаграмм рассеяния

Интерпретация приведенного рисунка такова: чем ближе к теоретической линии регрессии сгруппированы точки, тем теснее связь между изучаемыми показателями.

Шаг 6. Вернемся в окно Multiple Linear Regression (рисунок 3.4), для этого в окне Review Descriptive Statistic выберем кнопку Cancel (Отмена), далее снимем флажок с опции Review descriptive statistics, correlation matrix.

Нажав кнопку ОК, перейдем в следующее окно, содержащее результаты построения модели.

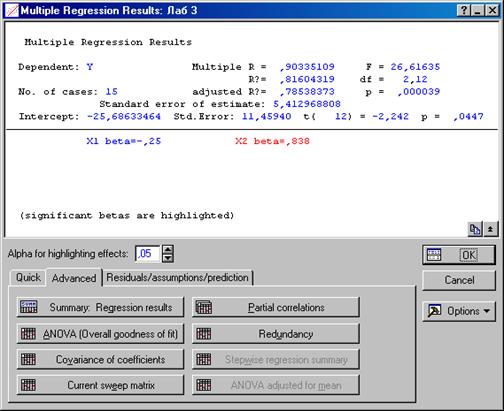
Рисунок 3.8 – Окно с результатами оценивания регрессии

где: Quick (Быстрые статистики) – данная вкладка предназначена для неопытных пользователей так как в ней доступна только одна кнопка Summary: Regression results. После ее инициализации в рабочую книгу выводятся две таблицы: таблица с коэффициентами и критериями, характеризующими качество уравнения регрессии; таблица с параметрами уравнения регрессии.

Advanced (Расширенные статистики) - вкладка предназначена для опытных исследователей, содержит дополнительные инструменты тестирования оцененной регрессионной модели.

Summary: Regression results (Вычислить: Результаты построения регрессии)

ANOVA (Overall goodness of fit)

Covariance of coefficients

Current sweep matrix

Partial correlations (Частная корреляция) – позволяет оценить корреляционную взаимосвязь зависимой и одной не зависимой переменными исключая влияние остальных переменных

Redundancy

Stepwise regression summary – результаты процедуры пошагового построения регрессии

ANOVA adjusted for mean

Residuals/assumptions/prediction (Отклонения / распределения / предсказания) – вкладка содержит алгоритмы анализа отклонений построенной модели, дескриптивные статистики, а также возможность рассчитывать прогнозные значения зависимой переменной.

Шаг 7. Выбрав кнопку Summary: Regression results (Вычислить: Результаты построения регрессии) перейдем в Workbook (Рабочая книга) где будут представлены две таблицы содержащие оцененные параметры модели и основные показатели адекватности построения регрессии.

Таблица 3.3 – Показатели адекватности множественного уравнения регрессии

	Value
Multiple R	0,903
Multiple R?	0,816
Adjusted R?	0,785
F(2,12)	26,616
p	0,000
Std.Err. of Estimate	5,413

Multiple R - Множественный коэффициент корреляции. Данный показатель является обобщением коэффициента линейной парной корреляции и отражает тесноту связи между зависимой переменной и одновременно несколькими независимыми пе­ременными. В отличие от парного коэффициента корреляции коэффициент множественной корреляции всегда неотрицате­лен и изменяется от 0 до 1. Чем ближе значение R к 1, тем большее одновременное влияние оказывают независимые пе­ременные.

В данном случае множественный коэффициент корреляции получен равным 0,903 показывает, что связь между вариацией результативного показателя Y и вариацией факторных признаков X1 и X2 сильная.

Multiple R? - Множественный коэффициент детерминации. Показатель измеряет долю полной вариации переменной Y, объясняемую множественной регрессией. Величина R² изменяется от 0 до 1. Если значение R² равно 1, то между переменными существует точная линейная связь. Если R² равно нулю, то статистическая линейная связь отсутствует.

Согласно данным таблицы 3.3, R² = 0,816 свидетельствует, что 81,6% вариации переменной Y объясняется факторами X1, X2.

Adjusted R? - Скорректированный коэффициент множественной детерминации 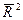. Важным свойством коэффициента детерминации является то, что R² - неубывающая функция от количества факторов, входящих в модель. Поэтому для сравнения коэффициентов детерминации разных моделей надо уравнивать количество факторов. Для сравнения моделей по коэффициенту детерминации корректируют коэффициент детерминации так, чтобы он как можно меньше зависел от количества факторов. Скорректированный коэффициент корреляции может быть использован для выбора лучшей модели.

F(2,12) - F- статистика Фишера, служит для проверки модели на адекватность. Для проверки модели на адекватность с помощью F - статистики Фишера используют значение вероятности p. Если значение вероятности меньше принятого значения a, например, 0,5, то нулевая гипотеза отвергается. Так в рассматриваемом примере p практически равна нулю. Следовательно, нулевая гипотеза о равенстве нулю всех коэффициентов регрессии отвергается. К аналогичному выводу можно прейти, если сопоставить табличное значение критерия при a=0,05 и v₁=2, v₂=12 равное 3,88 с фактическим значением F(2,12)= 26,616, т.е. получаем Fтаб < Fфакт следовательномодель в целом статистически значима.

Необходимо обратить внимание на то, что F-тест является суммарным тестом. Поэтому может возникнуть ситуация когда все t-статистики являются незначимыми, а F-статистика показывает адекватность модели, что и наблюдается в нашем случае (таблицу 3.4), отсюда можно сделать предположение о наличии мультиколлениарности (понятие будет введено в последующих лабораторных работах)

Таблица 3.4 – Результаты оценивания множественного уравнения регрессии

	Beta	Std.Err. of Betta	B	Std.Err. of B	t(12)	p-level
Intercept			-25,686	11,459	-2,242	0,045
X1	-0,253	0,125	-0,214	0,105	-2,032	0,065
X2	0,838	0,125	1,479	0,220	6,723	0,000

Рассмотрим результаты оценки параметров уравнения регрессии по столбцам. В первом столбце перечислены члены регрессионного уравнения, при этом Intercept это свободный член уравнения.

Во втором столбце содержатся b-коэффициент, являются отвлеченными (абстрактными) величинами и указывают на сколько среднеквадратических отклонений увеличится зависимая переменная при изменении соответствующего независимой переменной на 1 среднеквадратическое отклонение. На практике данный показатель используется для выявления фактора оказывающего наибольшее влияние на зависимую переменную. В нашем случае наибольшее (положительное) влияние оказывает показатель X2 (b₂=0,838).

В четвертом столбце содержатся значения параметров a_j оцененного уравнения вида 3.1, т.е. в данном случае получаем следующую регрессионную модель:

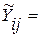-25,686 - 0,214×X1_ij + 1,479×X2_ij

Полученные значения параметров уравнения можно проинтерпретировать следующим образом. Если при прочих равных условиях (а₁ = - 0,214) среднечасовая производительность увеличится на 1 ед., то фондоотдача уменьшится на 0,214 руб./чел.

Если при прочих равных условиях удельный вес активной части ОПФ (а₂ = 1,479) увеличится на 1 процентный пункт, то фондоотдача увеличится на 1,479 руб./чел..

Std. Error (Standart error) указаны стандартные ошибки коэффициентов уравнения. Стандартные ошибки показывают статистическую надежность коэффициента. Если стандартные ошибки имеют нормальное распределение, то примерно в 2 случаях из 3 истинный коэффициент регрессора находится в пределах одной стандартной ошибки соответствующего коэффициента, и примерно в 95 случаях из 100 в пределах двух стандартных ошибок. Значение стандартных ошибок используем для построения доверительных интервалов.

t(12) – выводит расчетное значение t – статистики Стьюдента. Ее значение используется для проверки значимости соответствующего коэффициента.

p-level - показывает вероятность принять или отвергнуть гипотезу о равенстве нулю соответствующего коэффициента. При этом предполагается, что ошибки имеют нормальное или асимптотически нормальное распределение. Значения вероятности, указанные в таблице известны в статистике как уровни значимости a. Если значение вероятности ниже уровня значимости a, то гипотеза Н0 отвергается и соответствующий коэффициент не равен нулю.

Выделены те параметры модели, для которых гипотеза о значимости коэффициентов подтвердилась на 5% уровне значимости, т.е. значение Prob.< 0,05 и значения стандартной ошибки меньше оцениваемых коэффициентов в 2 раза и более.

В рассматриваемом примере параметр a₂ при переменной X2 значим при уровне значимости a больше, чем 0,0002. Коэффициент a₁ получен не значим при уровне a = 0,05, т.к. значение вероятности 0,065 больше 0,05.

Так же выявить статистическую значимость параметров можно использовав табличное значение t-критерия Стьюдента, в нашем случае при a=0,05 и df=12значение равно 2,1788, т.е. получаем:

а₀ – |-2,242| > 2,1788 Þ параметр статистически значим;

а₁ – |-2,032| < 2,1788 Þ параметр статистически не значим;

а₂ – |6,723| > 2,1788 Þ параметр статистически значим;

Шаг 8. Так как оцененная множественная регрессионная модель получена, незначима по параметру при X1, необходимо исключить из рассмотрения фактор X1. Для этого в активном окне выберем кнопку Cancel, перейдя в стартовое окно, далее в качестве независимой переменной (Independent var.) укажем X2. Получаем следующие результаты:

Таблица 3.5 – Показатели адекватности парного уравнения регрессии

	Value
Multiple R	0,868
Multiple R?	0,753
Adjusted R?	0,734
F(1,13)	39,571
p	0,000
Std.Err. of Estimate	6,030

Сравнивая показатели, полученные по первой и второй моделям можно заметить, что значения по второй модели снизились, но при этом модель в общем можно считать статистически значимой.

Согласно данным, приведенным в таблице 3.5, параметры парной регрессионной модель получены статистически значимыми.

Таблица 3.6 – Результаты оценивания парного уравнения регрессии

	Beta	Std.Err. of Betta	B	Std.Err. of B	t(12)	p-level
Intercept			-35,110	11,673	-3,008	0,010
X2	0,868	0,138	1,531	0,243	6,291	0,000

Оценив вторую модель, можно утверждать, что она пригодна для практического использования, так как параметры модели статистически значимы по t-критерию Стьюдента (таблица 3.6), а уравнение в целом проходит тест по F-критерию Фишера (таблица 3.5).