Кирхгофтың екінші заңы бойынша 5 страница

4.5-сурет. Параллельді тербелмелі контур.
Мұндай тізбекті параллель тербелмелі контур деп атайды. Резонанс кіріс реактивтік өткізгіштік тең:
 немесе
немесе  (4.7)
(4.7)
болған кезде басталады.
(4.7) ара қатынасқа  және
және  тізбектің параметрлары және жиілік арқылы көрсетілген мәндерін қойып, табамыз:
тізбектің параметрлары және жиілік арқылы көрсетілген мәндерін қойып, табамыз:
 (4.8)
(4.8)
(4.8) теңдеуді жиілік 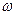 қарай шешемізде, резонанстық бұрыштық жиілік үшін келесі көріністі табамыз:
қарай шешемізде, резонанстық бұрыштық жиілік үшін келесі көріністі табамыз:
 (4.9)
(4.9)
Резонанс құбылысы мүмкін, егер де түбір астындағы көріністің (4.9) болымды таңбасы болса. Егер де  болса, онда тізбек қандайда болған жиілікте резонанс ережеде болады.
болса, онда тізбек қандайда болған жиілікте резонанс ережеде болады.
4.6-суретте резонанс кездегі векторлық диаграмма көрсетілген.

4.6-сурет. Тоқтар резонанс кездегі векторлық диаграмма.
Индуктивтік және сыйымдылық тармақтардағы тоқтар активтік  және реактивтік
және реактивтік  құрастырушылардан құрылады. Резонанс кезде
құрастырушылардан құрылады. Резонанс кезде  . Неғұрлым
. Неғұрлым  және
және 
 және
және  кіші болса, соғұрлым
кіші болса, соғұрлым  және
және  арасындағы фаза ығысу бұрышы
арасындағы фаза ығысу бұрышы  жақын. Егер де
жақын. Егер де  болса, онда тоқтар
болса, онда тоқтар  және
және  кернеуге қарағанда
кернеуге қарағанда 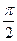 және
және  бұрыштарға ығысады, ал өз ара
бұрыштарға ығысады, ал өз ара  . Бұл жағдайда
. Бұл жағдайда  болады. Тізбектің кіріс кедергісі шексіз үлкен. Тармақтардағы тоқтар бір контурлық тоқты
болады. Тізбектің кіріс кедергісі шексіз үлкен. Тармақтардағы тоқтар бір контурлық тоқты  құрады да, ол тоқ контурдың ішінде тұйықталады.
құрады да, ол тоқ контурдың ішінде тұйықталады.
Идеалды параллельді контурдың (4.7-сурет), яғни  кезде, таратылмаған бөлігінде
кезде, таратылмаған бөлігінде  резонанстық қисықты саламыз.
резонанстық қисықты саламыз.

 |
4.7-сурет. Идеалды тербелмелі контур.
4.8-сурет. Резонанстық қисықтар.
Тоқ  , сондықтан
, сондықтан  қисық сәйкесті масштабта тоқтың резонанстық қисығы
қисық сәйкесті масштабта тоқтың резонанстық қисығы  болады. Жиілік
болады. Жиілік  кезде
кезде 


 тоқтар резонансы өтеді.
тоқтар резонансы өтеді.
Күрделі айнымалы тоқ электр тізбектерді есептеу әдістері:
а) контурлық тоқтар әдісі
Контурлық тоқтар және түйінді потенциалдар әдістерді күрделі тұрақты тоқ тізбектерді есептеу үшін қолдануы бірінші тарауда көрсетілген. Айнымалы тоқ тізбектерді есептеу кезде бұл әдістерде кең қолданады. Есептеуге қолданатын теңдеулерге кіретін шамалар комплексті түрде кіреді.
Контурлық тоқтар әдісі бойынша тармақтағы тоқтардың орнына Кирхгофтың екінші заңы бойынша контурларда тұйықталатын контурлық тоқтар анықталады.

4.9-сурет. Күрделі электр тізбектің сұлбасы.
 және
және  - конурлық тоқтар.
- конурлық тоқтар.  және
және  кедергілер арқылы өтетін
кедергілер арқылы өтетін  және
және  тоқтарға тең, ал
тоқтарға тең, ал  кедергі арқылы бұл тоқтардың бағыттарына қарап тоқтардың қосындысына немесе айырымына тең.
кедергі арқылы бұл тоқтардың бағыттарына қарап тоқтардың қосындысына немесе айырымына тең.
Контурлық тоқтар үшін жазылатын теңдеулер саны тәуелсіз конурлар санына тең, яғни түйіндер саны  және тармақтар саны
және тармақтар саны  бар электр тізбек үшін контурлық тоқтарды табуға
бар электр тізбек үшін контурлық тоқтарды табуға  теңдеуді құру керек.
теңдеуді құру керек.
Контурға кіретін комплекстік кедергілердің қосындысын контурдың өздік кедергісі деп, ал екі және одан көп контурларға жататын комплекстік кедергі – бұл контурлардың – ортақ кедергісі деп аталады.
Контурлық тоқтың болымды бағыты еркінше алынады.
Берілген электр сүлбе үшін (4.9-сурет) Кирхгофтың екінші заңы бойынша екі теңдеу жазылады:


мұнда  және
және  - I және II контурлардың өздік кедергілері;
- I және II контурлардың өздік кедергілері;  -I және II контурлардың ортақ кедергісі.
-I және II контурлардың ортақ кедергісі.
Егер де берілген электр сүлбеде  тәуелсіз контурлар болса, онда Кирхгофтың екінші заңы бойынша
тәуелсіз контурлар болса, онда Кирхгофтың екінші заңы бойынша  теңдеуден жүйе болады:
теңдеуден жүйе болады:
 (4.10)
(4.10)
мұнда  -
- 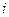 контурдағы контурлық ЭҚК
контурдағы контурлық ЭҚК  , яғни контурдағы ЭҚК-тердің алгебралық қосындысы;
, яғни контурдағы ЭҚК-тердің алгебралық қосындысы;
 -
- 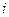 контурдың өздік кедергісі;
контурдың өздік кедергісі;
 -
- 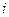 және
және  контурлардың ортақ кедергісі.
контурлардың ортақ кедергісі.
Контурлық тоқтарды (5.1) кернеулерді анықтауыштардың көмегімен табуға болады.
Жүйенің анықтаушысы


 ж.т.с
ж.т.с



б) түйіндік потенциалдар әдісі
Жоғарыда айтылғанда бұл әдіс Кирхгофтың бірінші заңын және Омның заңын қолдануға негізделген. Күрделі электр тізбектің қайсысы болған түйінің (базистік түйін) потенциалын нөлге тең деп алуға болады. Басқа түйіндермен базистік түінің арасындағы кернеу сол түйіндердің потенциалы болады. Бұл потенциалды тармақтың өткізгіштігіне көбейткенде сол тармақтағы тоқ табылады. Сонымен, егерде электр тізбектегі түйінді потенциалдарды тапсақ, онда тармақтардың тоқтарын табамыз.

4.10-сурет
Кирхгофтың бірінші заңы бойынша 1 және 2 түйіндер үшін  :
:











Егер де электр тізбекте  түйіндер болса, ал
түйіндер болса, ал  -ші түйіннің потенциалы нөлге тең болса, онда басқа түйіндердің
-ші түйіннің потенциалы нөлге тең болса, онда басқа түйіндердің  потенциалдарын табу үшін
потенциалдарын табу үшін  теңдеуді құру керек:
теңдеуді құру керек:
 (4.11)
(4.11)


 ж.т.с
ж.т.с



Бесінші тарау
5.1 Тізбектің индуктивтік байланысқан элементтері
Егер де тізбектің бір элементіндегі токтың өзгеруі тізбектің екінші элементінде ЭҚК-ті құруға келтірсе, онда бұл екі элемент индуктивті байланысқан болады, ал пайдалы болған ЭҚК өзара индукцияның ЭҚК-і деп аталады.
Тізбектің екі элементінің индуктивтік байланысы К байланыс коэфицентімен сипатталады
 (5.1)
(5.1)
мүндағы М-тізбектің элементтерінің өзара индуктивтігі; L1 және L2 -элементтердің индуктивтіктері.


5.1-сурет 5.2-сурет
5.1-суретте бірінші орауышта і1 ток аққан кездегі магнит өрістің суреті көрсетілген. Бірінші орауыштың орамдары Ф11 өздік индукциясының магнит ағынымен ілініскен, ал екінші орауыштың орамдары Ф21 өзара индукцияның магнит ағынымен ілініскен. Өздік және өзара индукцияның ағын ілінісулер
 (5.2)
(5.2)
мүндағы W1 және W2-орауыштардың орам сандары.
Бірінші орауыштың индуктивтігі және орауыштардың өзара индуктивтігі.

 (5.3)
(5.3)
5.2 – суретте екінші орауыштан  ток аққан кездегі магнит өрістің суреті көрсетілген
ток аққан кездегі магнит өрістің суреті көрсетілген

 (5.4)
(5.4)
Орауыштардың арасындағы индуктивтік байланыс орауыштарды бір-біріне жылжыту аркылы өзгертуге болады.
Өзара индукциямен себебші болған ЭҚК-тердің және кернеулердің абсолюттік мәндері (электромагнит индукциясының заңы),
 (5.5)
(5.5)
Бұл шамалардың таңбаларын білу үшін тізбектің индуктивтік байланысқан элементтерінің шықпаларын арнайы белгілейді.
Тізбектің индуктивтік байланыскан элементтердің екі шықпаларын аттас деп атайды және бірдей белгіше береді келесі тәртіпті қолданып: аттас шықпаларға қарай тоқтардың бағыттары бірдей болса әрбір элементте өздік және өзара индукциясының магнит ағындары қосылады.
Бұл тәртіпті 5.3, а-суретте көрсетілген орауыштардың шыкпаларын белгілеуге қолданамыз.
 |
Ток і1, шықпа а-дан шықпа в-ға бағытталғанда және ток і2 шықпа с-дан шықпа d-ға бағытталғанда өздік индукцияның ағындары Ф11 және Ф22 өзара индукцияның ағындары Ф12 және Ф21-лармен қосылады. Сондықтан а шықпа с шықпамен, ал в шықпа d шықпамен аттас.
5.3-сурет
Сурет 5.3,6 көрсетілген орауыштар үшін аттас болатын шықпалар а1 және d1, в1 және с1. Алдындағымен айырмасы екінші орауыштың орамдарының орау бағыты басқа болғанда.
Өздік индукциясының кернеулерінің және ЭҚК-терінің лезді мәндері.
 (5.6)
(5.6)
Комплексті мәндері үшін
 (5.7)
(5.7)
(5.7) көрініп түр U1M - кернеу І2 токтан p/2 немесе -p/2 бүрышка ығысып тұр. Бүл бұрыштың таңбасы аттас шықпаларға қарай U1M және I2M, болымды бағыттарының таңдауына тәуелді.  (шаманың өлшемі кедергіге тең [Ом]) өзара индукцияның кедергісі деп аталады да Хм деп бедгіленеді.
(шаманың өлшемі кедергіге тең [Ом]) өзара индукцияның кедергісі деп аталады да Хм деп бедгіленеді.  шама өзара индукцияның комплекстік кедергісі деп аталады да ZM белгіленеді.
шама өзара индукцияның комплекстік кедергісі деп аталады да ZM белгіленеді.
Сонымeн, ZМ =  =
=  (5.8)
(5.8)
5.1 Тізбектің индуктивтік байланысқан элементтердің тізбектеп және параллелді косылуы
Кедергілері R1 және R2 индуктивтіктері L1 және L2жәнe өзара индуктивтіктері М екі орауыш тізбектеп косылып тұр. Қосылудың екі түрі бар-келісімді (5.4,а-сурет) және қарсы (5.4,б-сурет).
 Келісімді косылған кезде әрбір уакытта екі элементтердегі токтардың бағыттары аттас шықпаларға қарай бірдей, сондықтан әрбір элементпен ілініскен өздік индукцияның магнит ағындары Ф11 (немесе Ф22 ) және өзара индукцияның магнит ағындары Ф12 (немесе Ф21) бір-бірімен қосылады. Қарсы косылғанда тізбектің екі элементтерінде әрбір уақытта аттас шықпаларға токтардың бағыттары қарама-қарсы, сондықтан әрбір элементпен ілініскен өздік индукцияның және өзара индукцияның магнит ағындары бір-бірінен алынады.
Келісімді косылған кезде әрбір уакытта екі элементтердегі токтардың бағыттары аттас шықпаларға қарай бірдей, сондықтан әрбір элементпен ілініскен өздік индукцияның магнит ағындары Ф11 (немесе Ф22 ) және өзара индукцияның магнит ағындары Ф12 (немесе Ф21) бір-бірімен қосылады. Қарсы косылғанда тізбектің екі элементтерінде әрбір уақытта аттас шықпаларға токтардың бағыттары қарама-қарсы, сондықтан әрбір элементпен ілініскен өздік индукцияның және өзара индукцияның магнит ағындары бір-бірінен алынады.
5.4-сурет
Екі тізбектеп косылған индуктивтік байланыскан элементтердің индуктивтігі  (5.9)
(5.9)
мұндағы  , және
, және  -бірінші және екінші элементтердің ағын ілінісулері, сонымен бірге
-бірінші және екінші элементтердің ағын ілінісулері, сонымен бірге  . Оң таңба келісімді қосылғанға, теріс таңба қарсы қосылғанға жатады. Сондыктан
. Оң таңба келісімді қосылғанға, теріс таңба қарсы қосылғанға жатады. Сондыктан
L = L1+L2  2М (5.10)
2М (5.10)
Элементтердегі кернеудің үш құраушылары бар:
 (5.11)
(5.11)
Тізбектің комплексті кіріс кедергісі, (5.11) еске алғанда, тең
 (5.12)
(5.12)
мұндағы 

5.5-сурет
5.5-суретте келісімді (а) және қарсы (б) қосылу үшін векторлык диаграммалар көрсетілген. 5.6-суретте тізбектің екі элементі (екі ораушы) кедергілері R1 және R2, индуктивтіктері L1 және L2, өзара индуктивтігі М параллельді қосылған, ал олардың аттас шыкпалары бір түйінге қосылған.
 (5.13)
(5.13)
мұндағы 
(5.13)теңдеулер жүйесін шешкенде, шығады:
 (5.14)
(5.14)

5.6-сурет
Тізбектің комплексті кіріс кедергісі
 (5.15)
(5.15)
Енді орауыштар 1 түйінге аттас емес шықпалармен қосылып тұрғанда қарайық.
 (5.16)
(5.16)
 (5.17)
(5.17)
5.3 Өзара индуктивтік бар кезде тармақталған тізбекті есептеу
Бұл жағдайда есептеу Кирхгофтың теңдеулері бойынша немесе контурлык ток әдісімен өткізіледі. Түйінді потенциалдар әдісі колданбайды.
Теңдеулерді Кирхгофтың екінші заңы бойынша құрғанда өзара индукцияның ЭҚК-і үйлесімді теңдеу ретінде есептеледі. К элементтегі ±  комплекстік кернeудің таңбасы К элементті аралап шығу бағытымен 8 элeменттегі токтың болымды бағытын салыстыру аркылы белгіленеді. Егер де бұл бағыттар аттас шықпаларға карай біршамада болса, онда кернеу тең
комплекстік кернeудің таңбасы К элементті аралап шығу бағытымен 8 элeменттегі токтың болымды бағытын салыстыру аркылы белгіленеді. Егер де бұл бағыттар аттас шықпаларға карай біршамада болса, онда кернеу тең  . Егер де ондай болмаса, онда кернеу тең ±
. Егер де ондай болмаса, онда кернеу тең ± 

Контурлык токгар үшін Кирхгофтың екінші заңы бойьнша теңдеулерді келтірейік: 

5.7-сурет
Қысқаша теңдеулерді былай жазуға болады:


Алтыншы тарау
6 Үшфазалы электр тізбектер
6.1 Үшфазалы электр тізбектер туралы түсінік
Үшфазалы электр тізбекті бір біріне  бұрышқа ығысқан бірдей жиіліктері бар ЭҚК-тер әрекет істейтін үш бірфазалы жиынтығы деп білуге болады. Бұл үшфазалы тізбектін үш бөлігі фазалар деп аталады (А,В және С фазалар).
бұрышқа ығысқан бірдей жиіліктері бар ЭҚК-тер әрекет істейтін үш бірфазалы жиынтығы деп білуге болады. Бұл үшфазалы тізбектін үш бөлігі фазалар деп аталады (А,В және С фазалар).
6.1-суретте фазалары электр байланыспаған үшфазалы тізбек көрсетілген. Мұндай үшфазалы тізбектер байлаулы емес деп аталады (қазіргі уақытта қолданбайды).

6.1-сурет. Байлаулы емес үшфазалы электр тізбек
ЭҚК-тердің амплитудалары және фазадағы кедергілер бірдей болғанда  токтардың шамалары бірдей және олар
токтардың шамалары бірдей және олар  бұрышқа ығысқан.
бұрышқа ығысқан.
Бұл токтардың қосындысы қандай болған уақыт мезгілде нөлге тең, сондықтан, егер де токтар қайтатын үш сымды біріктірсек, онда ол біріккен сымдағы ток нөлге тең болады, сол себептен ол сымды алып тастап 6.2-суреттегі тізбекке көшуге болады.

6.2-сурет. Байлаулы үшфазалы электр тізбек
Байлаулы үшфазалы электр тізбекті құру үшін үшфазалы синхронды генератор пайданалады. ЭҚК-терді түрлендіретін орамалар статордың ойықтарында орналасады. Фазалардың орамалары бір біріне қарай  бұрышқа ығысқан.
бұрышқа ығысқан.


6.3-сурет. Үшфазалы синхронды 6.4-сурет. Синхронды гене-
генератор ратордың векторлық диаграммасы
Ротор айналған кезде орамаларда амплитудалы және жиіліктері бір-біріне тең және  бұрышқа ығысқан Э.Қ.К-тер пайда болады. Бұл ЭҚК-терді бейнелейтін векторлар модуль (шама) бойынша бірдей және бір-біріне
бұрышқа ығысқан Э.Қ.К-тер пайда болады. Бұл ЭҚК-терді бейнелейтін векторлар модуль (шама) бойынша бірдей және бір-біріне  ығысқан (6.4-сурет). Үшфазалы генератордың лезді ЭҚК-тер 6.5-суретте көрсетілген, ал олардың аналитикалы көріністері:
ығысқан (6.4-сурет). Үшфазалы генератордың лезді ЭҚК-тер 6.5-суретте көрсетілген, ал олардың аналитикалы көріністері:
