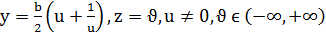Бет туралы түсінік. Бір тегіс беттер.
Ең қарапайым беттерден жазықтық, тұйық жарты жазықтық және квадратты айтамыз. Ең қарапайым беттерге гомеоморфты фигураны элементар бет деп айтамыз.
Басқаша айтқанда, элементар бет деп 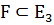 фигурасын айтамыз, егер ол екі өлшемді сызық
фигурасын айтамыз, егер ол екі өлшемді сызық 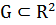 болса гомеоморфты болса.
болса гомеоморфты болса.
Евклид кеңістігіндегі 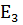 беттен ақырлы немесе санаулы элементар беттермен жабуға болатын
беттен ақырлы немесе санаулы элементар беттермен жабуға болатын 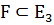 фигурасын айтамыз.
фигурасын айтамыз.
Егер әрбір нүктесінің маңайы элементар бет болса, онда ол бетті қарапайым деп атаймыз.
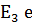 вклидтік кеңістігінде
вклидтік кеңістігінде 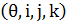 тік бұрышты координаттар жүйесін ендіреміз, онда элементар беттің теңдеуін келесі түрде беруге болады.
тік бұрышты координаттар жүйесін ендіреміз, онда элементар беттің теңдеуін келесі түрде беруге болады.
1. Векторлық теңдеуі: 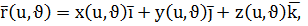
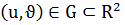
мұндағы 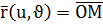 -
- 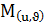 нүктесінің радиус векторы.
нүктесінің радиус векторы.
2. Параметрлік теңдеуі: 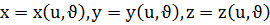
3. Айқындалмаған теңдеуі; 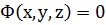
Параметрлік теңдеуі арқылы берілген F элементар беті 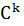 класына жататын біртегіс бет деп аталады.
класына жататын біртегіс бет деп аталады. 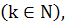 егер
егер 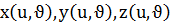 функциялары k реткіге дейін үзіліссіз дербес туындылары бар болып әрбір
функциялары k реткіге дейін үзіліссіз дербес туындылары бар болып әрбір 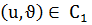 нүктесінде
нүктесінде 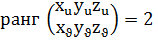 ғана орындалса.
ғана орындалса.
Айқындалмаған теңдеу арқылы арқылы берілген F беті 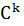 классына жататын бертегіс бет деп аталады, егер келесі екі шарт орындалса:
классына жататын бертегіс бет деп аталады, егер келесі екі шарт орындалса:
1) 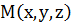 нүктесінің маңайында
нүктесінің маңайында 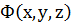 функциясы және оның k реткіге дейінгі дербес туындылары үзіліссіз болса;
функциясы және оның k реткіге дейінгі дербес туындылары үзіліссіз болса;
2) 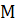 нүктесінде ранг
нүктесінде ранг 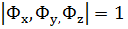 орындалсада.
орындалсада.
Егер векторлық функция арқылы теңдеуі берілген Г бетінде
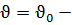 тұрақты деп алсақ, яғни,
тұрақты деп алсақ, яғни, 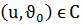 онда
онда 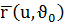 функциясы F бетінде жататын қандайда бір сызықты береді, оны u-сызығы деп атаймыз. Бұл сызықтың
функциясы F бетінде жататын қандайда бір сызықты береді, оны u-сызығы деп атаймыз. Бұл сызықтың 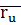 жанама векторы болады. Сол сияқты
жанама векторы болады. Сол сияқты 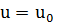 болған жағдайда.
болған жағдайда. 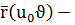 беттегі бір сызықтың теңдеуі болады, оны
беттегі бір сызықтың теңдеуі болады, оны 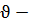 сызығы деп атаймыз.
сызығы деп атаймыз. 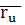 бұл сызықтың жанама векторы болады. Беттегі әрбір
бұл сызықтың жанама векторы болады. Беттегі әрбір 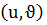 нүктесі арқылы біруден u және
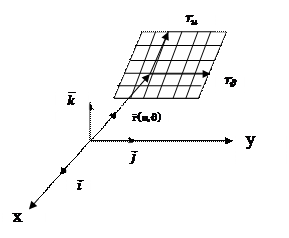
нүктесі арқылы біруден u және 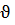 сызықтары өтеді. Осы сызықтарды беттегі координаттық сызықтар деп атаймыз. Бір тегіс беттегі
сызықтары өтеді. Осы сызықтарды беттегі координаттық сызықтар деп атаймыз. Бір тегіс беттегі 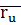 және
және 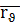 векторлары сызықты тәуелсіз векторлар болады: демек, біртегіс беттегі координаттық сызықтар әртүрлі бағыттарда өтеді екен.
векторлары сызықты тәуелсіз векторлар болады: демек, біртегіс беттегі координаттық сызықтар әртүрлі бағыттарда өтеді екен.
|

Егер 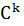 класына жататын
класына жататын 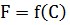 параметрлеу арқылы берілсе, ал
параметрлеу арқылы берілсе, ал 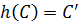 гомеоморфизм болса, онда
гомеоморфизм болса, онда
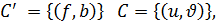 онда
онда 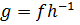 гомеоморфизмі анықталады. Егер g гомеоморфизмі
гомеоморфизмі анықталады. Егер g гомеоморфизмі 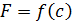 бетін анықтаса, онда h параметрлерді ауыстыру мүмкіндігінің гомеоморфизмі деп аталады.
бетін анықтаса, онда h параметрлерді ауыстыру мүмкіндігінің гомеоморфизмі деп аталады.
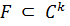 беті үшін
беті үшін 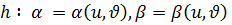 параметрін ауыстыру мүмкіндігіндегі бейнелуі деп аталады, егер келесі үш шарт орындалса:
параметрін ауыстыру мүмкіндігіндегі бейнелуі деп аталады, егер келесі үш шарт орындалса:
1) h - гомеомарфизм болса яғни 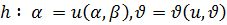
орындалса; 
2) 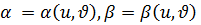 функцияларының k ретке дейінгі үзіліссіз дербес туындылары бар болса;
функцияларының k ретке дейінгі үзіліссіз дербес туындылары бар болса;
3) Әрбір нүктесі үшін 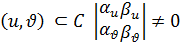 орындалса.
орындалса.
Мысалдар:
1. Келесі теңдеу арқылы берілген шеңберді OZ осі бойынша айналдырғанда пайда болған беттің параметрлік теңдеуін құрыңыздар:
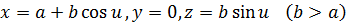
|
 Шешуі: Бастапқыда бұл беттің
Шешуі: Бастапқыда бұл беттің 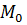 нүктесі бойында жатсын, яғни XOZ жазықтығында. t уақытынан кейін ол нүкте
нүктесі бойында жатсын, яғни XOZ жазықтығында. t уақытынан кейін ол нүкте 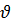 бұрышына бұрылым
бұрышына бұрылым 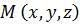 нүктесіне келеді. Бұрылу OZ осі бойынша болғандықтан нүкте OZ осіне перпендикуляр бұрылады, сондықтан нүктенің Z координатасы
нүктесіне келеді. Бұрылу OZ осі бойынша болғандықтан нүкте OZ осіне перпендикуляр бұрылады, сондықтан нүктенің Z координатасы 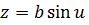 өзгермейді. Нүктенің траекториясы шеңбер болатыны белгілі және ол шеңбер xoy жазықтығына паралель, демек нүктенің координаттары
өзгермейді. Нүктенің траекториясы шеңбер болатыны белгілі және ол шеңбер xoy жазықтығына паралель, демек нүктенің координаттары 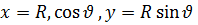 болады. R– айналу радиусы өзгермейді, демек
болады. R– айналу радиусы өзгермейді, демек 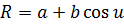 болады. Осыдан беттің теңдеуі келесі түрде болатынын көреміз.
болады. Осыдан беттің теңдеуі келесі түрде болатынын көреміз. 

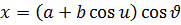
|
| |


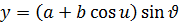
|



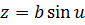
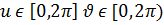
|
2. Келесі параметрлік теңдеулері арқылы берілген беттер беттесетінін дәлелдеңіздер.
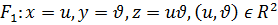
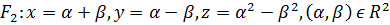
Шешуі: 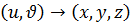 бейнелеуігомеоморфизм болады және
бейнелеуігомеоморфизм болады және 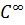 классына жатады, демек
классына жатады, демек 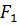 Беті бір тегіс себебі ранг
Беті бір тегіс себебі ранг 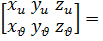 ранг
ранг 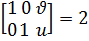
Осы сияқты 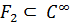 көреміз.
көреміз.
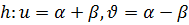 деп алсақ,
деп алсақ,
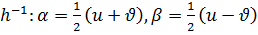 болып олар гомеоморфизмді анықтайды және
болып олар гомеоморфизмді анықтайды және 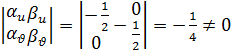
Демек 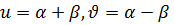 параметризация ауыстыруы мүмкін екен. Осыда бұл екі теңдеу бір бетті анықтайды.
параметризация ауыстыруы мүмкін екен. Осыда бұл екі теңдеу бір бетті анықтайды.
3. Келесі теңдеумен берілген бет бірқуысты гиперболлоидта анықтайтынын көрсетіңіз. Осы беттегі координаталық сызықтарды табыңыз:
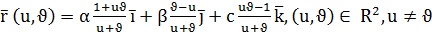
Шешуі: 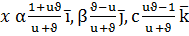 өрнектері
өрнектері 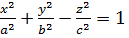 теңдеуін қанағаттандыратынын тексеріп көруге болады.
теңдеуін қанағаттандыратынын тексеріп көруге болады.
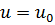 координаттық сызығының теңдеуі келесі түрде болады.
координаттық сызығының теңдеуі келесі түрде болады.
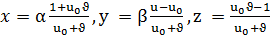 немесе
немесе 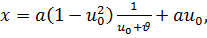
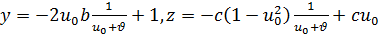 әрбір өрнектен
әрбір өрнектен 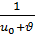 табатын болсақ,
табатын болсақ,
Келесі теңдікке келеміз.
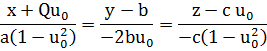
Бұл 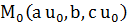 нүктесінен өтетін бағыттаушы векторы
нүктесінен өтетін бағыттаушы векторы
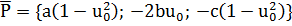
Осы сияқты 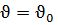 координаталық сызығын табамыз,
координаталық сызығын табамыз,
ол 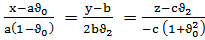
бұл сызықты 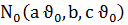 нүктесінен өтеді, бағыттаушы векторы
нүктесінен өтеді, бағыттаушы векторы
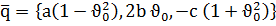
Сонымен бір қуысты гиперболлоидтық координаттық сызықтары түзу сызықтар болады, және бетте бұлардан өзгеше түзу сызықтар жоқ болады.
Жаттығулар:
1. Келесі сызықтардың қайсылары бір тегіс сызық болады? Болса қандай классқа жатады?
а) 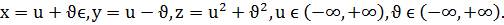
б) 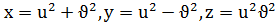
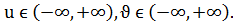
в) 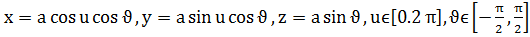 .
.
г) 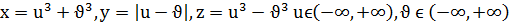 .
.
д) 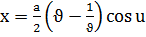 ,
, 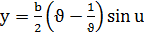 ,
, 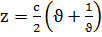 , u,
, u, 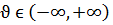
е) 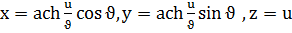
Жауаптары:
а) Болады 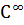 класына жатады;
класына жатады;
б) болмайды, кері бейнелері жоқ сондықтан гомеоморфизм болмайды
в) болады, 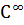 класына жатады;
класына жатады;
г) болмайды, функция 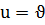 дифференцяланбайды;
дифференцяланбайды;
д) болмайды, функция 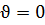 анықталмаған;
анықталмаған;
е) болады, 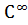 класына жатады.
класына жатады.
2. Параметрлік теңдеулері арқылы берілген келесі екінші ретті беттерді табыңыздар.
а) 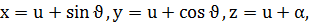 u,
u, 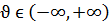
б) 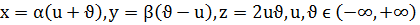
в) 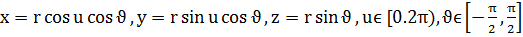 .
.
г) 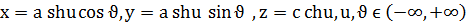
д) 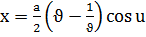 ,
, 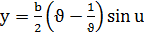 ,
, 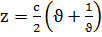 , u,
, u, 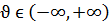
е) 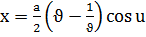 ,
, 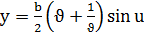 ,
, 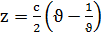 , u,
, u, 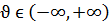
Жауаптары:
а) эллипстік цилиндр: 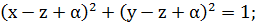
б) гиперболалық парабаллоид: 
в) сфера: 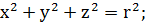
г) екі қуысты гиперболлоид: 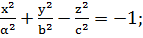
д)екі қуысты гирепболлоид: 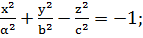
е) бір қуысты гиперболлоид: 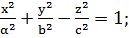
3. Параметрлері арқылы берілген беттердің теңдеулерін айқындалмаған түрде жазыңыздар:
а) 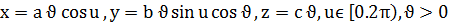
б) 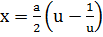 ,
, 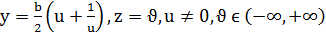
в) 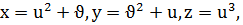 u,
u, 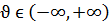
г) 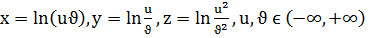
Жауаптары:
а) конус: 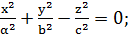
б) гиперболалық цилиндр: 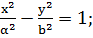
в) 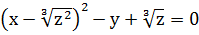
г)гиперболалық цилиндр: xy=z;
4. Келесі беттердің параметрлік теңдеуін жазыңыздар.
а) сфера;
б) эллипсоид;
в) екі қуысты гиперболлоид;
г) эллипстік параболлоид;
д) екінші ретті конус;
е) эллипстік цилиндр;
ж) гиперболалық цилиндр;
з) параболалық цилиндр.
Жауаптары:
а) 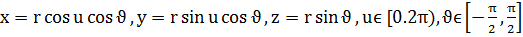
б) 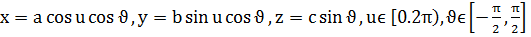
сфералық эллипсоидтың дербес түрі болатыны ескерілді;
в) 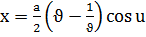 ,
, 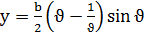 ,
, 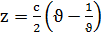 ,
, 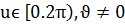
г) 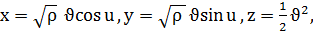
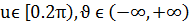
д) 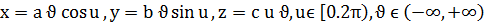
е) 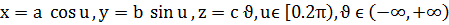
ж) 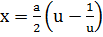 ,
,