Определение поперечных размеров

Требуемая площадь поперечного сечения i-ой ступени определяется по формуле

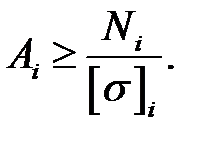
Учитывая заданные конструктивные ограничения по соотношению площадей ступеней, базовая площадь бруса А определяется в виде

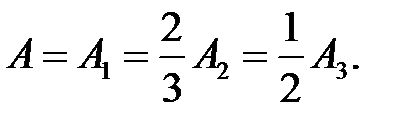
Требуемая по условию прочности базовая площадь поперечного сечения бруса в пределах I и II участков (первой ступени с материалом Ма1) рассчитывается исходя из наибольшей по абсолютной величине продольной силы N_i=N_II

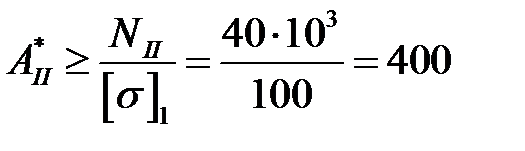мм².

Аналогично, исходя из наибольшей по абсолютной величине продольной силы N_i=N_IV=60кН в пределах III и IV участков второй ступени с материалом Ма2, имеем

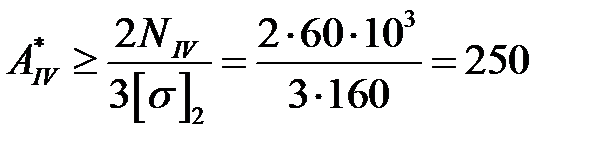мм².

Исходя из наибольшей по абсолютной величине продольной силы N_i=N_VI=100кН в пределах V и VI участков третьей ступени с материалом Ма3, для последней ступени бруса имеем

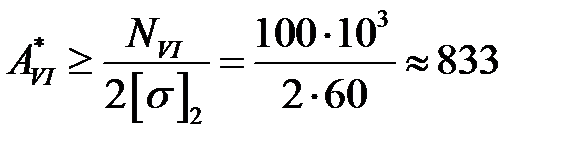мм².

Чтобы обеспечить прочность бруса при одновременном выполнении конструктивных ограничений по соотношению площадей ступеней, базовая площадь бруса А должна удовлетворять условию

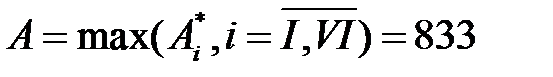мм².

Для дальнейших расчетов принимаем за базовую площадь бруса А=835мм².

Вычисление нормальных напряжений по участкам бруса в МПа

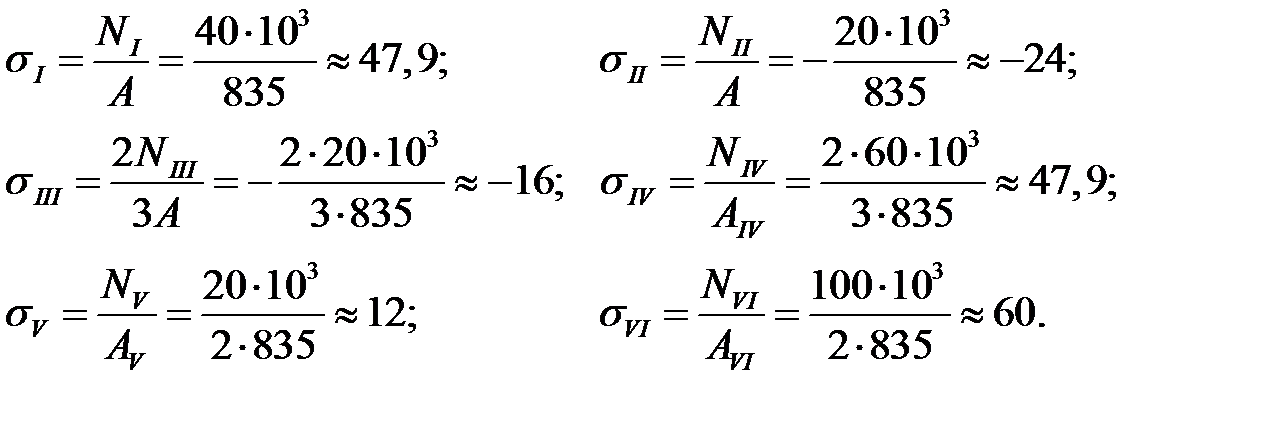
В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений (эпюра σ, рисунок 2.5).

Определение упругих перемещений бруса

Для определения упругих перемещений должно быть известно перемещение хотя бы одного из сечений бруса.

В сечении заделки (L) перемещение δ_L=0. Абсолютное удлинение участка VI (KL) определяется по закону Гука

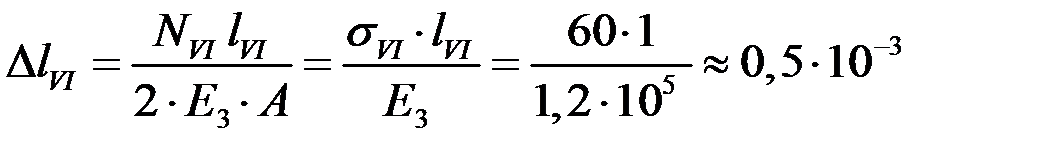м.

Тогда, перемещение сечения в (·) К

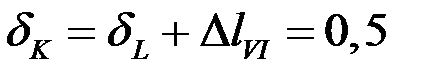мм.

Абсолютное удлинение участка V (LG) определяется в виде:

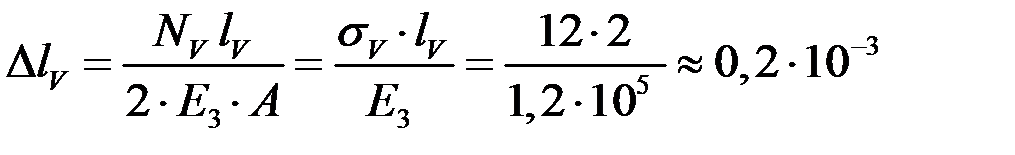м,

а перемещение сечения в (·) G

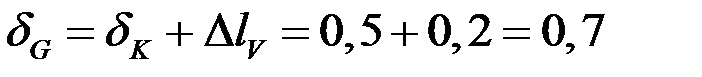мм.

Аналогично, нарастающим итогом определяются удлинения и упругие перемещения остальных участков:

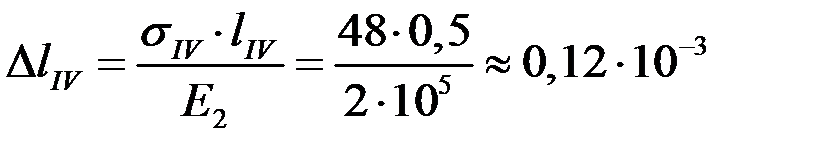м;

м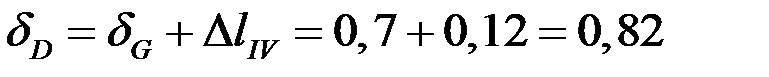м;

м;

мм;

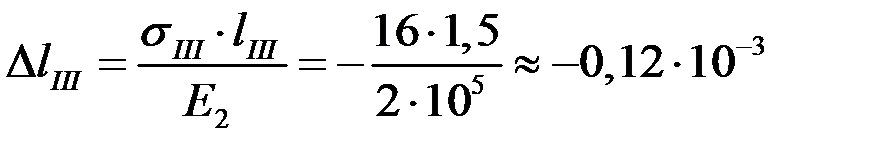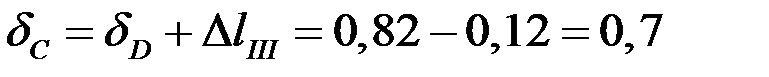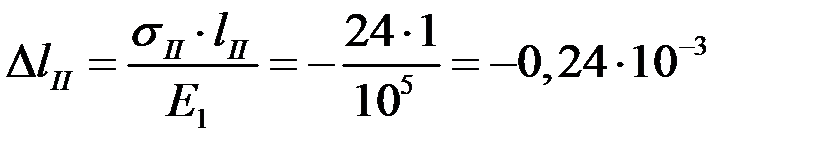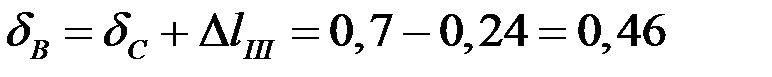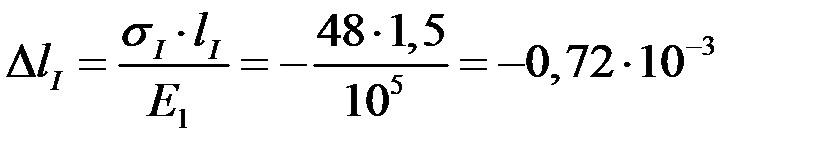м;

м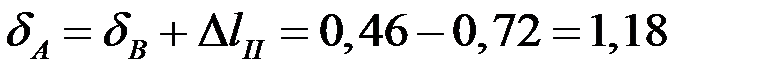м;

м;

мм.

Полное абсолютное удлинение бруса равно 1,18 мм.

В соответствии с полученными значениями упругих перемещений строим их эпюру (эпюра δ, рисунок 2.5).

№							F1	F2	F3	F4	F5
						0,5

Рисунок 2.5 – Эпюры продольной силы N, напряжений σ и перемещений δ.

Пример решения задачи 1.2

2.7

Дано: стержневая система, состоящая из абсолютно жесткой (заштрихованной) балки, удерживаемой тремя упругими стальными стержнями (рисунок 2.6а) одинакового поперечного сечения А1=А2=А3=А=200мм²;

допускаемое напряжение [σ]=160 МПа; модуль нормальной упругости E=2·10⁵ МПа;

a=b=1 м;

длина упругих стержней l1=l2=2 м.

Определить:

1) усилия, возникающие в упругих стержнях, выразив их через неизвестную нагрузку F;

2) допускаемую нагрузку [F] по условию прочности, приняв [σ] =160 МПа;

3) напряжения в стержнях при значении F=0,8[F];

4) определить вертикальное перемещение точки С.

Решение:

Предполагаем, что от внешней нагрузки все упругие стержни испытывают растяжение. Разрезаем стержни в узлах крепления, заменяя их по методу сечений продольными силами (Рисунок).

Усилия в стержнях определятся из условий равновесия нижней отсеченной части системы:

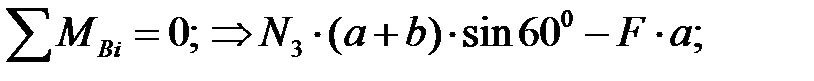
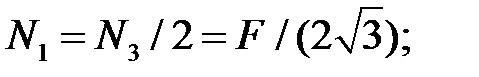
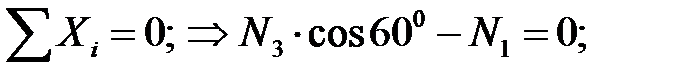
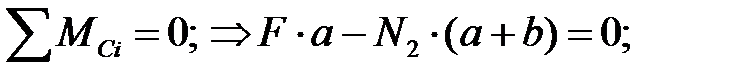
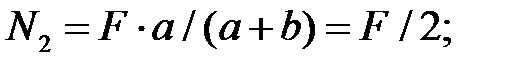
Проверка: сумма проекций всех сил на ось Y должна быть равна нулю:

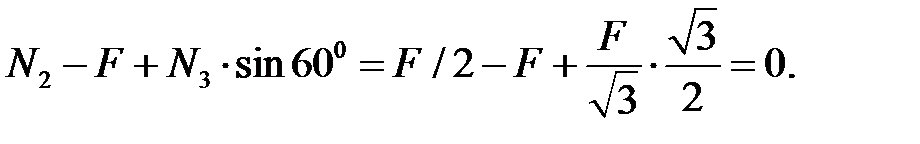
Вычислим напряжения, возникающие в каждом стержне:

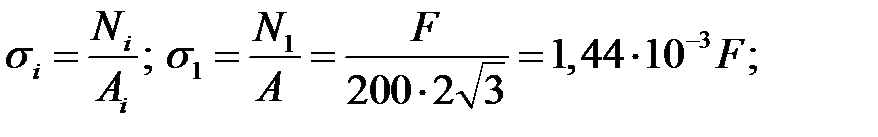
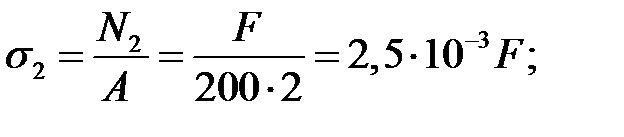
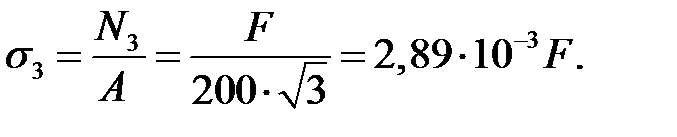
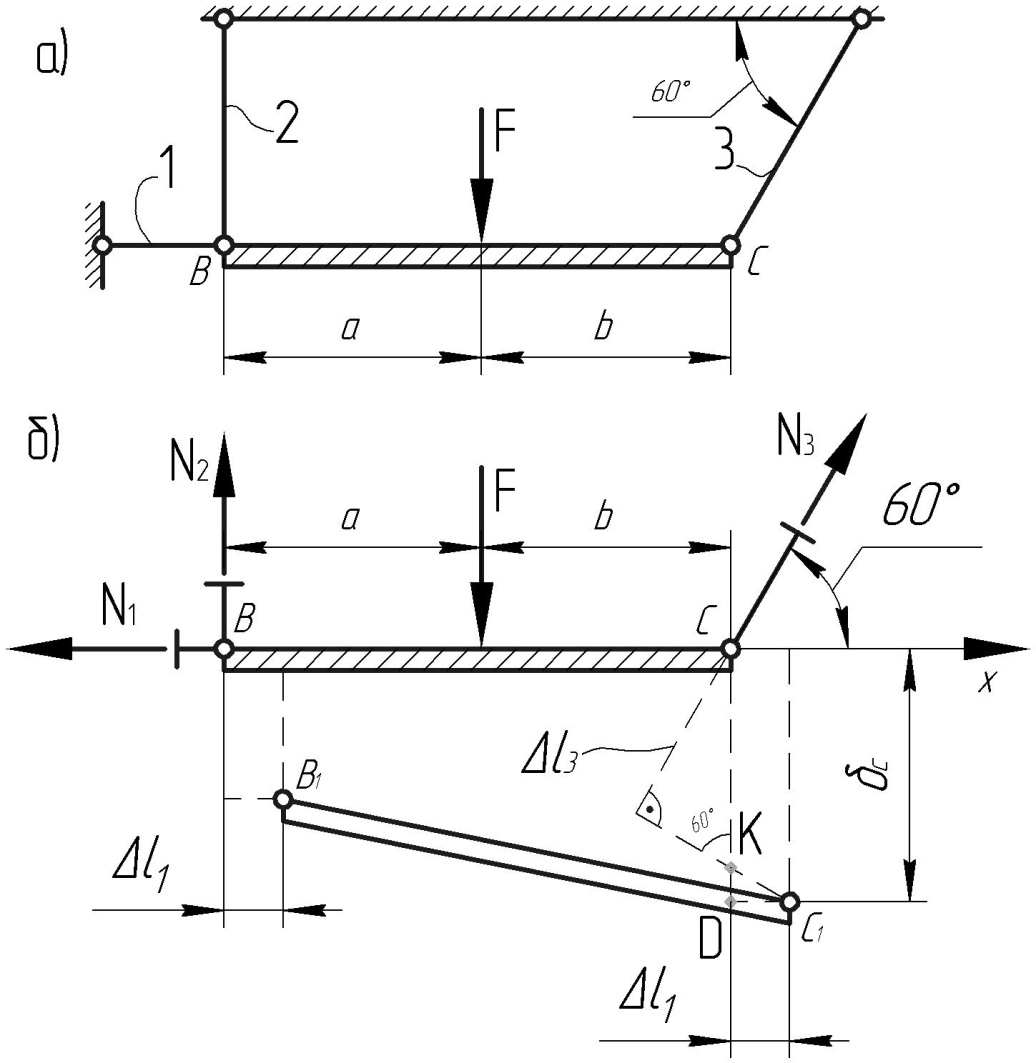
а) расчетная схема; б) деформированная схема стержневой системы

Рисунок 2.6 – Расчетные схемы

Наиболее напряженным оказался третий стержень. По условию прочности

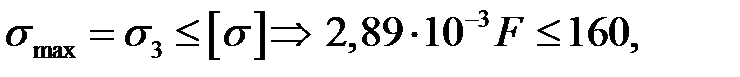
откуда, 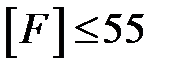кН. Принимаем [F]=55кН.

Вычислим напряжения, возникающие в каждом стержне при F=0,8[F]=44кН:

σ₁=63,4 МПа, σ₂=110 МПа,

σ₃=127,2 МПа.

Для определения вертикального перемещения точки С вычислим удлинения стержней (рисунок 2.6б):

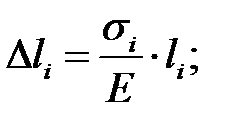
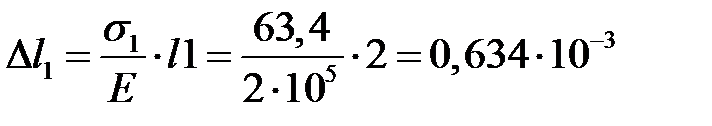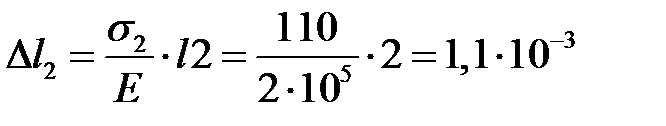м;

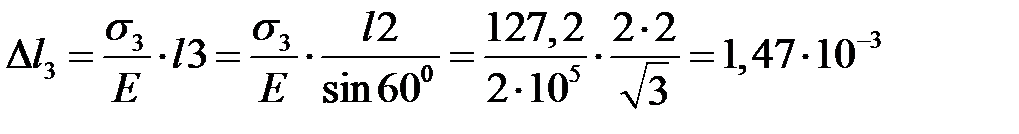м;

м.

Из геометрии деформированного состояния системы (рисунок 2.4б), имеем:

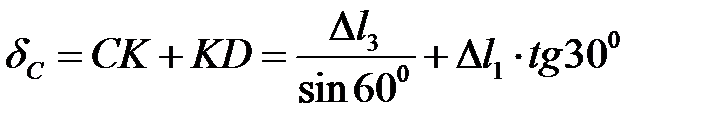
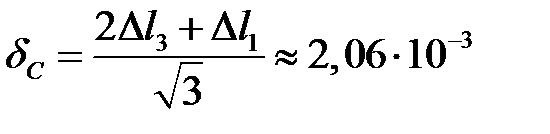м

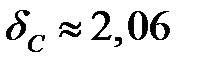или мм.

2.6 ЗАДАЧА № 1.3 Расчет статически неопределимой шарнирно – стержневой системы

Дано: Статически неопределимая шарнирно - стержневая система, нагруженная сосредоточенной силой F и состоящая из невесомой, абсолютно жесткой балки АВ, которая опирается на шарнирно-неподвижную опору и поддерживается двумя стальными стержнями.

Соотношение площадей поперечных сечений стержней заданы.

Исходные данные для решения задачи в соответствии с индивидуальным шифром варианта задания указаны в Приложении Б3.

Требуется:

1) составить в масштабе индивидуальную расчетную схему задачи;

2) определить степень статической неопределимости;

3) раскрыть статическую неопределимость – определить продольные силы натяжения стержней;

4) подобрать размеры сечений стержней в форме квадрата;

5) определить напряжения в стержнях:

¾ от действия силы F;

¾ при нагреве заданного i-го стержня;

¾ при сборке системы в результате неточности изготовления длины заданного i-го стержня.