Глава 2. тепловое расширение твердых и жидких тел 1 страница
Сборник задач по теплофизике
| |
Содержание
Глава 1. ТЕПЛОТА.. 3
Основные понятия, законы и формулы.. 3
Решение задач. Примеры.. 4
Задачи к главе 1. 12
Глава 2. ТЕПЛОВОЕ РАСШИРЕНИЕ ТВЕРДЫХ И ЖИДКИХ ТЕЛ.. 15
Основные понятия, законы и формулы.. 15
Решение задач. Примеры.. 15
Задачи к главе 2. 19
Глава 3. ГАЗЫ... 21
Основные понятия, законы и формулы.. 21
Решение задач. Примеры.. 23
Задачи к главе 3. 33
Глава 4. НАСЫЩАЮЩИЕ И НЕНАСЫЩАЮЩИЕ ПАРЫ. ВЛАЖНОСТЬ.. 40
Основные понятия, законы и формулы.. 40
Решение задач. Примеры.. 41
Задачи к главе 4. 45
Глава 1. ТЕПЛОТА
Основные понятия, законы и формулы
1. Все тела состоят из атомов и молекул, находящихся в непрерывном беспорядочном движении. Хаотическое движение молекул тела называют тепловым движением. Каждая молекула вещества обладает кинетической и потенциальной энергией, поэтому всякое тело, наряду с механической энергией направленного движения частиц, обладает внутренней энергией.
В молекулярной физике под внутренней энергией подразумевают часть ее: кинетическую энергию хаотического движения микрочастиц (молекул, атомов, ионов, свободных электронов) и потенциальную энергию их взаимодействия друг с другом. Все другие виды внутренней энергии тел (энергия электромагнитного излучения, электронных оболочек, внутриядерная) считаются неизменными и не влияющими на рассматриваемые процессы:
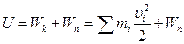
Изменение внутренней энергии и передача ее от одного тела к другому происходит в процессе взаимодействия тел. Есть два способа, две формы такого взаимодействия. При первом способе внутренняя энергия одного тела изменяется за счет изменения энергии упорядоченного (механического) движения частиц другого тела (механической работы, электризации, перемагничивания, облучения).
Мерой изменения энергии упорядоченного движения частиц вещества в процессе макроскопического взаимодействия тел служит работа А. Во втором случае изменение внутренней энергии происходит вследствие соударения хаотически движущихся молекул соприкасающихся тел.
Процесс изменения внутренней энергии тела, обусловленный передачей теплового движения молекул без совершения работы внешней средой, называют тепловым процессом или процессом теплопередачи.
Мерой взаимодействия тел, приводящего к изменению энергии хаотического движения и взаимодействия молекул (мерой энергии хаотического движения, переданной от одного тела к другому в процессе теплообмена), служит величина Q, называемая количеством теплоты.
2. Количество теплоты, подведенное к телу (системе тел) идет в общем случае на изменение внутренней энергии тела и на совершение телом работы над внешними телами (первое начало термодинамики – закон сохранения и превращения энергии с учетом тепловых явлений):
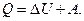 (1.1)
(1.1)
Количество теплоты Q, сообщенное телу, считают при этом положительным, отданное телом – отрицательным. Работу считают положительной, если тело за счет своей внутренней энергии совершает работу над внешней средой, и отрицательной, если работа совершается над телом и за счет работы увеличивается внутренняя энергия.
Количество теплоты и работа являются мерами изменения внутренней энергии, количество теплоты – в процессе теплопередачи, работа – в процессе превращения механической энергии в теплоту.
3. Если при подведении к телу количества теплоты Q температура тела повышается на 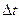 , то теплоемкость тела в рассматриваемом процессе равна:
, то теплоемкость тела в рассматриваемом процессе равна:
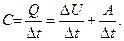 (1.2)
(1.2)
Удельная теплоемкость тела массой m:
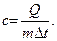 (1.3)
(1.3)
Если суммарная кинетическая энергия теплового движения молекул изменяется при неизменной потенциальной энергии, то изменение внутренней энергии тела массой m, равно:
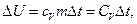 (1.3’)
(1.3’)
где 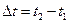 – изменение температуры тела, cV – удельная теплоемкость и CV – теплоемкость тела, взятые при постоянном объеме (А=0).
– изменение температуры тела, cV – удельная теплоемкость и CV – теплоемкость тела, взятые при постоянном объеме (А=0).
4. Тела могут находиться в одном из трех агрегатных состояний – твердом, жидком или газообразном – и при определенных условиях могут переходить из одного состояния в другое. Эти превращения происходят или в процессе теплообмена тела с окружающими телами, или вследствие перераспределения внутренней энергии в самом теле.
а) При плавлении кристаллических тел за счет теплоты, подводимой к телу (при А=0), потенциальная энергия атомов или молекул вещества, имеющего массу m, возрастает на величину
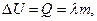 (1.4)
(1.4)
где l - удельная теплота плавления.
В процессе кристаллизации потенциальная энергия уменьшается на такую же величину, и соответствующее количество теплоты отводится к окружающим телам. Кинетическая энергия атомов при этом почти не меняется.
б) Если при испарении жидкости образуется пар массой m, то потенциальная энергия молекул пара увеличивается, а кинетическая энергия молекул, остающихся в жидкости, уменьшается на величину
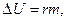 (1.5)
(1.5)
где R — удельная теплота испарения. Внутренняя энергия системы пар — жидкость при этом остается неизменной. Если процессу испарения сопутствует теплообмен с окружающей средой, в результате которого температура жидкости остается постоянной, то количество подводимой к ней теплоты определяется той же формулой (1.5).
При образовании пара массой m в процессе кипения жидкости внутренняя энергия молекул возрастает на величину
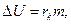
где Rk – удельная теплота кипения, являющаяся частным значением удельной теплоты испарения жидкости для температуры кипения. Внутренняя энергия системы в процессе кипения (при А=0) увеличивается за счет подвода к жидкости соответствующего количества теплоты извне.
в) В процессе химического соединения у ряда веществ перестраивается структура молекул, в результате чего резко увеличивается их кинетическая энергия. Такие процессы называют процессами горения, а участвующие в них тела – топливом и окислителем.
При полном сгорании топлива массой m внутренняя энергия теплового движения молекул возрастает на величину
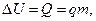 (1.6)
(1.6)
где q – удельная теплота сгорания топлива при данном окислителе.
Решение задач. Примеры
1. Решение задач этой главы основано на уравнении закона сохранения и превращения энергии с учетом формул изменения внутренней энергии тел и некоторых уравнений механики. Умение правильно применять закон сохранения энергии к конкретным физическим процессам представляет основную трудность при решении задач на теплоту. Особое внимание здесь нужно обратить на различие между количеством теплоты и изменением внутренней энергии и на выбор системы тел (или тела), для которой составляется основное уравнение. Нередко возникают затруднения при числовых расчетах в задачах, связанных с превращением одного вида энергии в другой. Здесь нужно помнить, что в уравнении (1.1) закона сохранения и превращения энергии все три величины Q, ΔU и А должны быть выражены в одних единицах.
2. Задачи об изменении внутренней энергии тел можно разделить на три группы. В задачах первой группы рассматривают такие явления, где в изолированной системе при взаимодействии тел, изменяется лишь их внутренняя энергия без совершения работы над внешней средой. Одни из тел, участвующих в теплообмене, при этом охлаждаются, другие – нагреваются. Согласно закону сохранения и превращения энергии (1.1) для тел, внутренняя энергия которых уменьшается, можно записать:
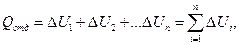 (1.7)
(1.7)
поскольку ни сами тела, ни над телами работу не совершают (A=0).
Аналогично для тел, энергия которых возрастает, мы получим:
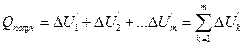 (1.7´)
(1.7´)
Из определения понятия количества теплоты и закона сохранения энергии как следствие вытекает:
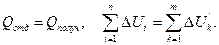 (1.8)
(1.8)
Перенеся все члены в левую часть равенства, уравнение (7.8) представим в ином виде:
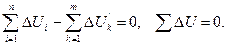 (1.8´)
(1.8´)
Последнее уравнение является очевидным следствием первого начала термодинамики – в изолированной системе тел, где происходят только процессы теплопередачи, внутренняя энергия системы не изменяется и, следовательно, алгебраическая сумма изменений энергии отдельных тел равна нулю.
Уравнение (1.8) называют уравнением теплового баланса, оно обычно служит основным расчетным соотношением для всех задач первой группы.
Правила их решения состоят в следующем:
а) Прочитав условие задачи, нужно установить, у каких тел внутренняя энергия уменьшается, у каких – возрастает. Особое внимание следует обращать на то, происходят ли в процессе теплообмена агрегатные превращения или нет.
б) Составить уравнения (1.7) для тел, энергия которых уменьшается, (1.7´)–для тел, энергия которых возрастает, и приравнять полученные суммы.
При записи уравнения теплового баланса в виде (1.8) нужно в выражении 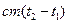 для изменения внутренней энергии всегда вычитать из большей температуры тела меньшую и суммировать все члены арифметически, если же уравнение записывается в виде (1.8), необходимо вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака.
для изменения внутренней энергии всегда вычитать из большей температуры тела меньшую и суммировать все члены арифметически, если же уравнение записывается в виде (1.8), необходимо вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака.
В ряде задач задается к.п.д. теплообмена; в этом случае его всегда нужно ставить сомножителем перед 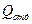 .
.
При определенном навыке можно составлять уравнение (1.8) или (1.8´) теплового баланса сразу, не прибегая к промежуточным выкладкам. Практически при решении задач удобнее пользоваться первым из этих уравнений.
3. В задачах второй группы рассматривают явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел. Результат такого взаимодействия – изменение внутренней энергии одного тела вследствие совершенной им или над ним работы. Теплообмен между телами здесь, как правило, не учитывают.
Уравнение закона сохранения и превращения энергии в этом случае имеет вид:
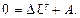 (1.9)
(1.9)
Решение таких задач удобно проводить по следующей схеме.
а) Анализируя условие задачи, нужно прежде всего установить, у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом. Кроме того, следует убедиться, что в процессе взаимодействия тел теплота извне к ним не подводится, т. е. действительно ли Q=0.
б) Записать уравнение (1.9) для тела, у которого изменяется внутренняя энергия, учтя знак перед А и к.п.д. рассматриваемого процесса. При записи уравнения (1.9) с учетом к.п.д. удобно поступать так. Если по смыслу задачи работа совершается за счет уменьшения внутренней, энергии одного из тел и по каким-либо причинам лишь часть ее идет на совершение работы A, то
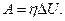 (1.9´)
(1.9´)
Если же из условия видно, что внутренняя энергия тела увеличивается за счет работы, совершенной над телом, и по каким-либо причинам лишь часть ее идет на увеличение U, то
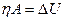 (1.9´´)
(1.9´´)
в) Составив уравнение (1.9) или (1.9´´), нужно найти выражение для А и ΔU.
Для А возможно одно из следующих соотношений:
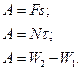
Для ΔU чаще всего достаточно использовать одну из формул:
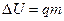 (сжигание топлива);
(сжигание топлива);
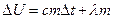 (нагрев и плавление тела);
(нагрев и плавление тела);
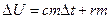 (нагрев и испарение).
(нагрев и испарение).
Подставляя в исходное уравнение вместо А и ΔU их выражения, получим окончательное соотношение для определения искомой величины. Если в условиях задачи даются дополнительные условия, то к основному уравнению следует, как обычно добавить вспомогательные.
г) Далее нужно выписать числовые значения известных величин, проверить число неизвестных в уравнениях и решить систему уравнений относительно искомой величины.
4. Задачи третьей группы объединяют в себе две предыдущие. В этих задачах рассматривают взаимодействие трех и более тел. В процессе такого взаимодействия к одному из тел подводится некоторое количество теплоты Q, в результате чего изменяется его внутренняя энергия и совершается работа.
Для решения этих задач надо составить полное уравнение закона сохранения и превращения энергии (1.1). Составление такого уравнения включает в себя приемы, описанные в п. 2 и 3.
Пример 1.В закрытом медном калориметре массой mM=200 г находится лед массой 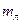 =1 кг при температуре
=1 кг при температуре 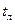 = -10°С. В калориметр впускают пар массой
= -10°С. В калориметр впускают пар массой 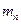 =200 г, имеющий температуру
=200 г, имеющий температуру 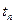 =110°С. Какая температура установится в калориметре? Удельную теплоемкость паров воды в интервале от 100 до 110°С считать равной
=110°С. Какая температура установится в калориметре? Удельную теплоемкость паров воды в интервале от 100 до 110°С считать равной 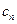 =1.7·103 дж/(кг град).
=1.7·103 дж/(кг град).
Решение. а) Примем систему пар – лед — калориметр за изолированную и будем считать, что с окружающей средой ее теплообмен ничтожно мал и им можно пренебречь. В такой системе полная внутренняя энергия остается неизменной, так как Q=0 и А=0.
Основным уравнением, описывающим процесс теплового взаимодействия между телами системы, здесь является уравнение теплового баланса с учетом агрегатных превращений. Поскольку в данном примере произведение 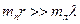 , нетрудно заметить, что при установившейся температуре в калориметре будет находиться вода при температуре, большей 0°С.
, нетрудно заметить, что при установившейся температуре в калориметре будет находиться вода при температуре, большей 0°С.
б) При тепловом взаимодействии со льдом и калориметром внутренняя энергия молекул пара уменьшается: при охлаждении от начальной температуры 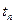 до температуры конденсации
до температуры конденсации 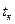 =100°С на величину
=100°С на величину 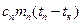 , при конденсации пара в воду – на величину
, при конденсации пара в воду – на величину 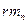 , при дальнейшем охлаждении образовавшейся воды от температуры
, при дальнейшем охлаждении образовавшейся воды от температуры 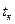 до окончательно установившейся температуры
до окончательно установившейся температуры 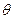 – на величину
– на величину 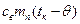 . В результате внутренняя энергия горячего тела – пара уменьшится на
. В результате внутренняя энергия горячего тела – пара уменьшится на
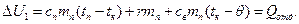
За счет этой энергии калориметр нагревается от начальной температуры, равной температуре льда 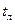 , до окончательной
, до окончательной 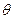 его внутренняя энергия увеличивается на величину
его внутренняя энергия увеличивается на величину 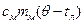 . Кроме того, часть энергии пара переходит ко льду. Энергия молекул льда возрастает: при нагревании от начальной температуры
. Кроме того, часть энергии пара переходит ко льду. Энергия молекул льда возрастает: при нагревании от начальной температуры 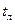 до температуры плавления
до температуры плавления 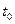 =0°С на величину
=0°С на величину 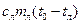 , в процессе плавления – на величину
, в процессе плавления – на величину 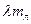 и при дальнейшем нагревании образовавшейся воды – на величину
и при дальнейшем нагревании образовавшейся воды – на величину 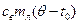 .
.
В результате внутренняя энергия холодных тел возрастает на
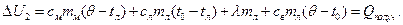
Так как 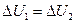 , то уравнение теплового баланса для данного процесса будет иметь вид:
, то уравнение теплового баланса для данного процесса будет иметь вид:
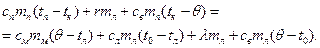
Решая это уравнение относительно 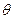 и подставляя числовые данные, взятые из условия задачи и из таблиц, находим:
и подставляя числовые данные, взятые из условия задачи и из таблиц, находим:
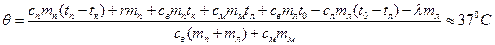 .
.
Анализируя полученное выражение, можно заметить, что при достаточно большой массе пара 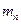 температура
температура 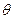 может оказаться больше начальной температуры пара
может оказаться больше начальной температуры пара 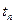 , чего в действительности быть не может. Такой результат объясняется тем, что после теплообмена при установившейся температуре одновременно могут существовать две фазы вещества: жидкость и пар, если при охлаждении пар не полностью конденсируется в воду. Уравнение теплового баланса в этом случае будет отличаться от того, которое мы составили. Чтобы не делать лишних вычислений, во всех сомнительных случаях, когда трудно определить, окажется ли вещество в одном или двух агрегатных состояниях, рекомендуется сделать предварительную числовую прикидку – сколько теплоты требуется для нагревания холодного тела до температуры соответствующего превращения (плавления или кипения) и сколько теплоты может выделиться горячим телом при остывании или при полной конденсации (кристаллизации). Сразу в общем виде такие задачи решать нельзя. Если окажется, что
, чего в действительности быть не может. Такой результат объясняется тем, что после теплообмена при установившейся температуре одновременно могут существовать две фазы вещества: жидкость и пар, если при охлаждении пар не полностью конденсируется в воду. Уравнение теплового баланса в этом случае будет отличаться от того, которое мы составили. Чтобы не делать лишних вычислений, во всех сомнительных случаях, когда трудно определить, окажется ли вещество в одном или двух агрегатных состояниях, рекомендуется сделать предварительную числовую прикидку – сколько теплоты требуется для нагревания холодного тела до температуры соответствующего превращения (плавления или кипения) и сколько теплоты может выделиться горячим телом при остывании или при полной конденсации (кристаллизации). Сразу в общем виде такие задачи решать нельзя. Если окажется, что 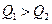 , то после перераспределения энергии получится одна фаза вещества, если же будет
, то после перераспределения энергии получится одна фаза вещества, если же будет 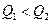 , то при установившейся температуре будут находиться две фазы – пар и жидкость (жидкость и лед).
, то при установившейся температуре будут находиться две фазы – пар и жидкость (жидкость и лед).
Пример 2.При соблюдении необходимых предосторожностей вода может быть переохлаждена до T1=–10°С. Сколько льда образуется из такой воды массой m0=1 кг, если в нее бросить кусочек льда и этим вызвать замерзание воды? Какую температуру должна иметь переохлажденная вода, чтобы она целиком превратилась в лед? Удельная теплоемкость переохлажденной воды 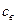 =4.19·103дж/(кг град), льда
=4.19·103дж/(кг град), льда 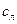 =2.1·103 дж/(кг град). Удельная теплота плавления льда λ=3.3·105 дж/кг.
=2.1·103 дж/(кг град). Удельная теплота плавления льда λ=3.3·105 дж/кг.
Решение. Для того чтобы при охлаждении вода замерзла, в ней должны находиться неоднородные включения, около которых начинается рост кристалликов льда. При отсутствии центров кристаллизации воду можно охладить до температуры значительно ниже 0°С. Такая вода называется переохлажденной.
Если в переохлажденной воде искусственно создать центры кристаллизации, в ней начнет образовываться лед. Молекулы станут переходить в состояние, соответствующее минимуму их потенциальной энергии. Уменьшение потенциальной энергии одной части молекул, образующих лед, вызывает увеличение теплового движения остальных молекул, которое регистрируется нами как нагревание воды. Так как взаимодействием переохлажденной воды с окружающей средой по условию задачи можно пренебречь, то в результате частичной кристаллизации воды в ней произойдет только перераспределение энергии. Полная внутренняя энергия останется неизменной, и, следовательно, уменьшение потенциальной энергии молекул будет равно увеличению их кинетической энергии.
Задача сводится к составлению уравнения теплового баланса при условии, что Q=0, А=0 с учетом агрегатного превращения.
При образовании из переохлажденной воды льда массой m2 потенциальная энергия молекул уменьшится на величину
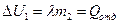 .
.
Эта энергия пойдет на нагревание образовавшегося льда от начальной температуры T1 до температуры T0=0°С и нагревание оставшейся после кристаллизации воды массой m1 на T0-T1 градусов (дальнейшее нагревание невозможно, так как при 0°С кристаллизация льда прекратится). Таким образом, вследствие нагревания внутренняя энергия теплового движения молекул увеличится на
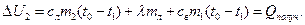
По закону сохранения энергии 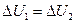 , поэтому уравнение теплового баланса будет иметь вид:
, поэтому уравнение теплового баланса будет иметь вид:
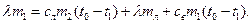 (1)
(1)
Кроме того,
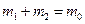 . (2)
. (2)
Из соотношений (1)–(2) находим массу образовавшегося льда:
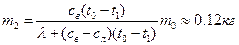 .
.
Чтобы замерзла вся переохлажденная вода, энергия, выделившаяся при кристаллизации, должна полностью пойти на нагревание образовавшегося льда, т. е.
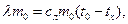 (3)
(3)
где Tх — начальная температура переохлажденной воды. Из последнего уравнения находим:
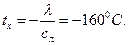
Пример 3.В колбе находилась вода при T=0°С. Выкачиванием из колбы воздуха заморозили всю воду в сосуде. Какая часть воды при этом испарилась, если притока теплоты извне не было? Удельная теплота испарения воды при 0°С R=24.8·105 дж/кг. Удельная теплота плавления льда 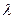 =3.3·105 дж/кг.
=3.3·105 дж/кг.
Решение. При испарении воды вылетают наиболее быстрые молекулы, вследствие чего суммарная кинетическая энергия оставшихся молекул уменьшается и температура воды понижается. Если из сосуда, в котором происходит испарение, откачивать пары воды и свести до минимума теплообмен с окружающей средой, то кинетическая энергия оставшихся молекул может уменьшиться настолько, что они образуют твердую фазу воды – лед. Поскольку в данном процессе тепло извне не подводится (Q=0) и работа не совершается (А=0), то внутренняя энергия всех молекул остается, постоянной, изменение потенциальной энергии вылетающих молекул воды 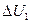 равно изменению потенциальной энергии
равно изменению потенциальной энергии 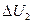 оставшихся, так как температура жидкости не изменяется.
оставшихся, так как температура жидкости не изменяется.
При образовании пара массой 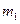 потенциальная энергия молекул пара возрастает на величину
потенциальная энергия молекул пара возрастает на величину
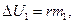
В процессе образования льда массой 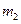 потенциальная энергия молекул уменьшается на
потенциальная энергия молекул уменьшается на
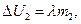
Поскольку 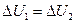 , то
, то
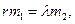 (1)
(1)
причем 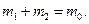 (2)
(2)
По условию задачи дам нужно определить отношение
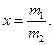
Из соотношений (1)–(2) находим:
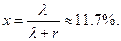
Пример 4.В дьюаровском сосуде, содержащем жидкий азот при температуре 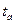 =195°С, за время
=195°С, за время 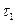 =24 ч испаряется азот объемом
=24 ч испаряется азот объемом 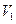 =1 дм3 при температуре окружающего воздуха
=1 дм3 при температуре окружающего воздуха 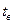 =20°С. Определите удельную теплоту парообразования азота, если известно, что при температуре
=20°С. Определите удельную теплоту парообразования азота, если известно, что при температуре 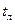 =00C в том же сосуде за время
=00C в том же сосуде за время 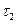 ==22.5 ч тает лед массой
==22.5 ч тает лед массой 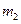 =40 г. Считать, что скорость подвода теплоты внутрь сосуда пропорциональна разности температур снаружи и внутри сосуда. Плотность жидкого азота
=40 г. Считать, что скорость подвода теплоты внутрь сосуда пропорциональна разности температур снаружи и внутри сосуда. Плотность жидкого азота 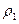 =0.8 г/см3, удельная теплота плавления льда
=0.8 г/см3, удельная теплота плавления льда 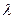 =3.3·105 дж/кг.
=3.3·105 дж/кг.
Решение. Вследствие того, то дьюаровский сосуд не является идеальным теплоизолятором, между телами, находящимися в сосуде, и окружающей средой происходит теплообмен. Так как работа при этом не совершается, то ОСНОВБЫМ уравнением, описывающим процесс теплопередачи при испарении азота и плавлении льда, служит уравнение теплового баланса:
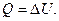
В результате теплообмена хранящиеся в сосуде холодные тела нагреваются и могут переходить из одного агрегатного состояния в другое. Теплота, подводимая извне, идет на увеличение внутренней энергии этих тел, причем согласно условию задачи
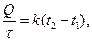
где 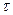 – время в течение которого к сосуду подводится количество теплоты Q (
– время в течение которого к сосуду подводится количество теплоты Q ( 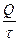 – скорость подвода теплоты); k – коэффициент пропорциональности, зависящий от устройства и материала сосуда;
– скорость подвода теплоты); k – коэффициент пропорциональности, зависящий от устройства и материала сосуда; 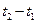 – разность температур снаружи и внутри сосуда.
– разность температур снаружи и внутри сосуда.
К. жидкому азоту за время 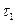 подводится количество теплоты, равное
подводится количество теплоты, равное
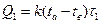 .
.
