Б) случай зонально- неоднородного пласта.
Отчет по лабораторной работе №6
На тему
«Исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в неоднородном пласте»
По дисциплине: ____Подземная гидромеханика_ ___
(наименование учебной дисциплины согласно учебному плану)
Выполнил: студент гр. НГ-09-2_ /Чеботов А. Ю./
(подпись) (Ф.И.О.)
Проверил:преподаватель /Гладков П.Д./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
Цель:исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в неоднородном пласте.
Теоретические сведения:
Рассмотрим особенности фильтрации в слоисто- неоднородных и зонально-неоднородных круговых пластах:
А) случай слоисто-неоднородного пласта
1. Распределение давления в каждом из пропластков носит логарифмический характер и определяется выражением:
Распределение давления в круговом пласте:
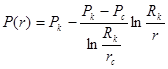 ,где (1)
,где (1)
P(r) - установившееся давление на расстоянии г от скважины. Па:
Рк - установившееся контурное (пластовое) давление на контуре питания rk, Па;
Рг - установившееся давление в скважине, Па;
гс - радиус скважины, м;
R- радиус контура питания пласта, м;
r - текущий радиус, м.
Градиенты давления в каждом пропластке постоянны и равны между собой:
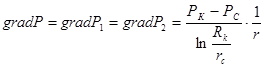 (2)
(2)
Скорости фильтрации по пропласткам:
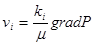 (3)
(3)
При равенстве градиентов давления в каждом пропластке из формулы 2 следует справедливость следующего соотношения:
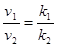 (4)
(4)
Т.е. для слоисто-неоднородного пласта скоростифильтрации по пропласткам прямо пропорциональны проницаемостям.
Дебит потока Q можно вычислить как сумму дебитов в отдельных пропластах Q1 и Q2:
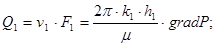 (5)
(5)
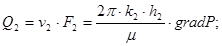 (6)
(6)
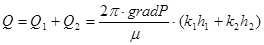 , (7) где B- ширина пласта, м;
, (7) где B- ширина пласта, м;
h1, h2– толщина пропластков, м.
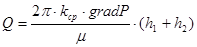 (8)
(8)
Приравняв уравнение 8 и 9, получим средний коэффициент проницаемости:
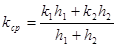 .
.
б) случай зонально- неоднородного пласта.
Для начала определим давление 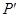 на границе между зонами, основываясь на уравнении неразрывности
на границе между зонами, основываясь на уравнении неразрывности 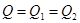 .
.
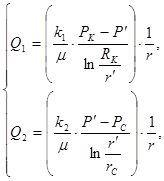
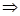
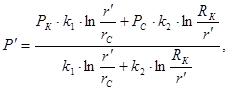 (9)
(9)
Распределение давления в каждой из зон носит логарифмический характер и определяется выражениями:
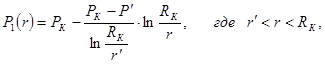 (10)
(10)
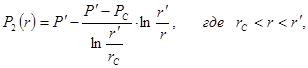 (11)
(11)
Градиенты давления в каждой зоне постоянны, но не равны между собой, поскольку:
gradP1 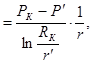 (12)
(12)
gradP2 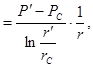 (13)
(13)
Скорости фильтрации по зонам соответственно:
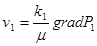 (14)
(14)
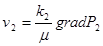 (15)
(15)
Дебит потока в силу установившегося движения несжимаемой жидкости будет постоянен через любую цилиндрическую поверхность, соосную скважине:
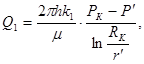 (16)
(16)
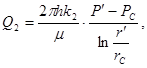 (17)
(17)
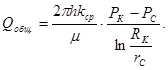 (18)
(18)
Определение средней проницаемости пласта:
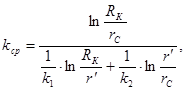 (19)
(19)
Задачи лабораторной работы:
1) изучение влияния изменения проницаемости на распределение давления в слоисто- и зонально-неоднородных круговых пластах при установившейся фильтрации в них несжимаемой жидкости;
2) изучение характера изменения градиента давления и скорости фильтрации по радиусу слоисто- и зонально-неоднородных круговых пластов при установившейся фильтрации в них несжимаемой жидкости;
3) определение средней проницаемости слоисто- и зонально-неоднородных круговых пластов.
Таблица 1
Исходные данные
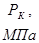 | 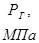 | 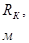 | 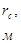 | 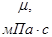 | 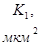 | 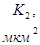 | Слоисто-неоднородный | Зонально-неоднородный | |
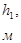 | 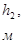 | 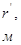 | |||||||
| 9,7 | 7,2 | 0,18 | 2,0 | 0,7 | 0,4 |
где 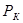 – давление на контуре питания;
– давление на контуре питания;
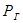 – давление на стенке галереи;
– давление на стенке галереи;
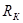 – радиус контура питания;
– радиус контура питания;
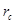 – радиус скважины;
– радиус скважины;
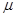 – динамическая вязкость жидкости;
– динамическая вязкость жидкости;
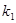 ,
, 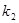 – проницаемость пропластков или зон пласта;
– проницаемость пропластков или зон пласта;
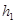 ,
, 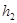 – толщина пропластков;
– толщина пропластков;
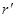 – радиус границы между первой и второй зонами пласта.
– радиус границы между первой и второй зонами пласта.
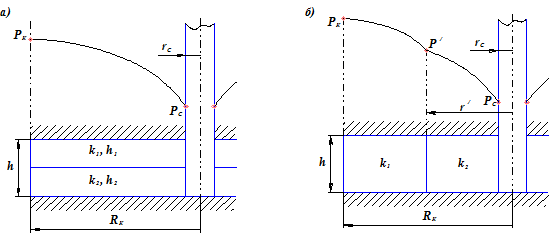
Рис.1.Схема плоскорадиального фильтрационного потока в слоисто-неоднородном (а) и зонально-неоднородном (б) пластах.
Расчеты:
