Генеральная и выборочная совокупности

Генеральной совокупностью называется вся подлежащая изучению совокупность объектов (наблюдений). Один или несколько элементов, взятых из генеральной совокупности для получения информации о ней, называется выборочной совокупностью или выборкой. Объемом совокупности (выборочной или генеральной) называется число элементов этой совокупности.

Метод статистического исследования, состоящий в том, что на основе изучения выборки делается заключение обо всей генеральной совокупности, называется выборочным. Для того чтобы по отобранным значениям некоторого показателя можно было достаточно уверенно судить обо всей совокупности, полученная выборка должна быть репрезентативной (представительной), т.е. правильно отражать пропорции генеральной совокупности. Выборка будет представительной лишь тогда, когда все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.

В дальнейшем под генеральной совокупностью будем подразумевать не само множество объектов, а множество значений случайной величины, принимающей числовое значение на каждом из объектов. В статистике обычно исследуемые случайные величины называют признаками и обозначают большими латинскими буквами 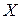, 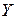и т.д.

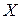Выборку будем рассматривать как совокупность независимых случайных величин , распределенных так же, как и случайная величина (признак) , представляющая генеральную совокупность.Конкретные значения, которые приняли эти случайные величины в результате эксперимента, называют реализацией выборки или значениями признака и обозначают строчными буквами . Различные значения признака называют вариантами.

Вариационные ряды

Числа, показывающие, сколько раз встречаются варианты в выборке, называются частотами (обозначаются ).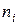

Вариационным (статистическим) рядом называется расположенный в порядке возрастания или убывания ряд вариант с соответствующими им частотами. Вариационный ряд часто называют рядом распределения выборки.

Вариация (изменение) количественных признаков может быть дискретной, например, академическая система успеваемости: 5 – отлично, 4 – хорошо и т.д., или непрерывной, например, возраст, рост или вес человека. В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.

Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину. Он представляет собой таблицу, состоящую из двух строк: конкретных значений признака и их частот:

			…
			…

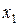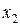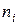где .

Вариационный ряд называется интервальным, если варианты могут отличаться один от другого на сколь угодно малую величину[1]. Он представляет собой таблицу, состоящую из двух строк – интервалов значений признака и числа значений выборки, попадающих в этот интервал:

Интервал,			…
Частота,			…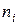

Числовые характеристики

Вариационный ряд содержит достаточно полную информацию об изменчивости признака. Однако обилие числовых данных, с помощью которых он задается, усложняет их использование. В то же время на практике часто оказывается достаточным знание лишь сводных числовых характеристик выборочной совокупности. Рассмотрим наиболее часто используемые числовые характеристики вариационных рядов: среднюю арифметическую, дисперсию и среднее квадратическое отклонение.

Средняя арифметическая

Средние величины характеризуют значения признака, вокруг которого концентрируются наблюдения. Наиболее распространенной из средних величин является средняя арифметическая. Для ее расчета используют формулу:

, (14)

где – варианты, 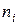– соответствующие им частоты, 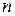– объем совокупности.

Если средняя арифметическая рассчитывается по всей генеральной совокупности в целом, то ее называют генеральной средней, а если по выборке – выборочной средней.

Если статистический материал представлен в виде интервального вариационного ряда, то при расчете выборочной средней сначала необходимо вычислить середины каждого интервала , которые рассчитываются по формуле: . Далее расчеты ведутся, как и для дискретного вариационного ряда, но в качестве вариантов используем .

Дисперсия и среднее квадратическое отклонение

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формуле:

. (15)

Дисперсия, рассчитанная для генеральной совокупности, называется генеральной дисперсией, а для выборки – выборочной дисперсией.

При вычислении выборочной дисперсии для интервальных вариационных рядов в качестве , как и при вычислении выборочной средней, используются середины соответствующих интервалов.

Иногда, особенно если дисперсию приходится рассчитывать «вручную», удобнее использовать другую формулу, которая легко получается из формулы (15) с помощью несложных математических преобразований:

. (16)

Среднее квадратическое отклонение представляет собой квадратный корень из дисперсии:

.

Среднее квадратическое отклонение (СКО) выражается в тех же единицах измерения, что и признак.

Точечные оценки

Большинство случайных величин имеют распределения, зависящие от одного или нескольких параметров. Так, например, нормальное распределение зависит от параметров 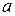и .

Выборочная характеристика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется статистической точечной оценкой этого параметра. Статистическая оценка неизвестных параметров теоретического распределения генеральной совокупности (или просто параметров генеральной совокупности) – одна из основных задач математической статистики.

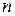Обозначим через некоторый неизвестный параметр генеральной совокупности, а через – точечную оценку этого параметра. Оценка есть функция от выборки объема из независимых случайных величин , каждая из которых имеет тот же закон распределения, что и генеральная совокупность. Поэтому оценка , как функция случайных величин, также является случайной величиной, в отличие от оцениваемого параметра , который является величиной неслучайной, детерминированной.

Оценка для параметра называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е. . В противном случае оценка называется смещенной.

Несмещенность – свойство оценок при фиксированном 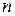. Оно означает отсутствие ошибки "в среднем", т.е. при систематическом использовании данной оценки.

Рассмотрим некоторые наиболее часто встречающиеся точечные оценки параметров генеральной совокупности.

1. Выборочная средняя 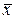есть несмещенная оценка для генеральной средней 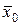, причем , где – объем выборки, – генеральная дисперсия признака.

2. Выборочная дисперсия является смещенной оценкой генеральной дисперсии .

3. Исправленная дисперсия , вычисляемая по формуле

(17)

или

, (18)

является несмещенной оценкой для генеральной дисперсии .

Разница между и заметна при небольшом числе наблюдений . При получим, что , т.е. в качестве оценки вполне можно использовать выборочную дисперсию .

Интервальные оценки

Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема точность обычно бывает достаточной, то для выборок небольшого объема вопрос точности оценок становится очень важным.

Чтобы получить представление о точности и надежности оценки параметра , используют интервальную оценку параметра.

Интервальной оценкой параметра называется числовой интервал , который с заданной вероятностью накрывает неизвестное значение параметра , т.е. . Такой интервал называется доверительным, а вероятность – доверительной вероятностью или надежностью оценки.

Обычно надежность оценки задается заранее величиной, близкой к единице, например: 0,9, 0,95, 0,99 или 0,999.

Границы доверительного интервала и его длина находятся по выборочным данным и поэтому являются случайными величинами. Длина доверительного интервала уменьшается с ростом объема выборки 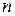и увеличивается с ростом доверительной вероятности .

Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно несмещенной точечной оценки , т.е. выбирается интервал вида . Число при этом называется точностью оценки.

Так, например, интервальная оценка (доверительный интервал) для генеральной средней 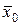исследуемого признака 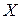, имеющего нормальное распределение, может быть найдена по формуле:

. (19)

В случае, когда генеральная дисперсия известна (например, это заранее заданная ошибка измерительного прибора), то точность оценки находится по формуле:

, (20)

где 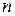– объем выборки, а число определяется из равенства , т.е. по таблице значений функции Лапласа находится значение аргумента , которому соответствует значение функции , равное .

В случае, когда генеральная дисперсия неизвестна, а известна лишь ее оценка – исправленная выборочная дисперсия , то точность оценки находится по формуле:

, (21)

где значение числа определяется по таблице критических точек распределения Стьюдента при доверительной вероятности и числе степеней свободы .

Замечание. Если выборка объема 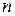представляет собой набор независимых одинаково распределенных случайных величин, то, согласно центральной предельной теореме, распределение при больших 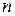близко к стандартному нормальному. Это позволяет строить доверительный интервал для генеральной средней 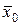по формулам (19) и (20) при любом распределении признака, если объем выборки является достаточно большим ( ), при этом в качестве используется ее любая оценка.