Геометрический смысл производной

Геометрическая интерпретация производной состоит в следующем: значение производной функции 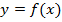в точке 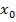равно угловому коэффициенту касательной, проведенной к графику функции в той же точке 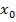, то есть:

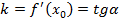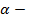, где угол между положительным направлением оси 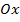и касательной к графику функции 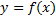в точке .

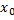Уравнение касательной имеет вид:

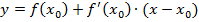
Примеры решения задач

Пример 1. Составьте уравнение касательной к графику функции

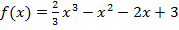в точке с абсциссой .

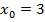Решение:

Найдем ординату точки касания: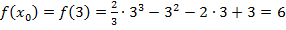

Найдем значение производной в точке :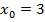

; .

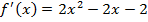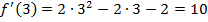Имеем искомое уравнение: 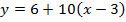, то есть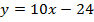

Исследование функций и построение графиков

Общая схема исследования функции:

1. Найти область D(y), то есть те значения x, при которых функция определена.

2. Определить является ли функция чётной или нечётной.

Если f(-x)=f(x), то функция чётная (график будет симметричен относительно Оy)

Если f(-x)= - f(x), то функция нечётная (график будет симметричен относительно О)

3. Определить (если не затруднительно) точки пересечения с осями координат

С осью Оx: y=0, находим значение x С осью Оy: x=0, находим значение y

Найти асимптоты, если они имеются.

Наклонная асимптота – прямая вида 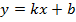, где ,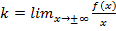

.

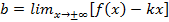Вертикальная асимптота – прямая вида 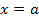, если .

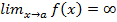Горизонтальная асимптота – прямая вида 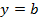, если .

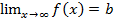5. Найти критические точки функции:

а) находим производную функции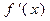

б) приравниваем производную к нулю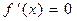

6. Определить промежутки монотонности функции:

Разбиваем область определения на интервалы и определяем знак производной в каждом из интервалов:

Если 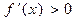, то f(x) ­, если 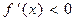, то f(x) ¯

7. Определить экстремумы функции,то есть определяем точки min и max, вычисляем значение функции в этих точках.

8. Найти критические точки 2 рода:

а) находим вторую производную функции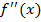

б) приравниваем вторую производную к нулю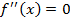

9. Определить промежутки вогнутости, выпуклости, точки перегиба:

а) разбиваем область определения на интервалы и определяем знак второй производной в каждом из интервалов.

Если, 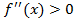то f(x)È , если, 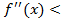то f(x)Ç

б) определяем точки перегиба и вычисляем значение функции в них

Построить график

Используя результаты исследования, соединяем полученные точки плавной кривой. Иногда для большей точности графика находят несколько дополнительных точек.

Примеры решения задач

Пример 1.Исследовать функцию и построить ее график.

Решение:

1. .

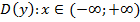2. Имеем: . Функция не является ни четной, ни нечетной, так как 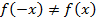и .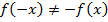

3. Найдем точки пересечения графика функции с осями координат.

С осью Ox: 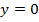, получаем уравнение: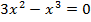

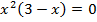
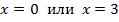
Значит 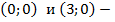точки пересечения с осью Ox.

С осью Oy: 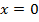, из равенства получаем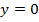

Значит (0;0) 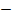точка пересечения с осью Oy.

4. Асимптот нет.

5. а)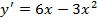

б)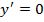

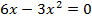
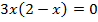
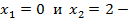критические точки функции

6. Область определения функции разделится на три промежутка, определяем знак производной в каждом:

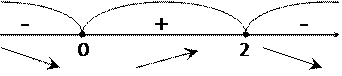При 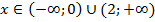функция убывает

При 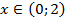функция возрастает

7. Точки экстремума: 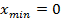, тогда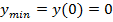

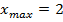, тогда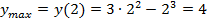

8. а)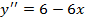

б)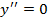

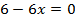
критическая точка II рода

9. Область определения функции разделится на два промежутка, определяем знак второй производной в каждом:

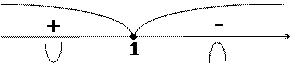При 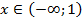функция выпукла вниз

При 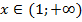функция выпукла вверх

При 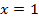имеем точку перегиба, ее ордината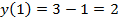

10. Построим график:

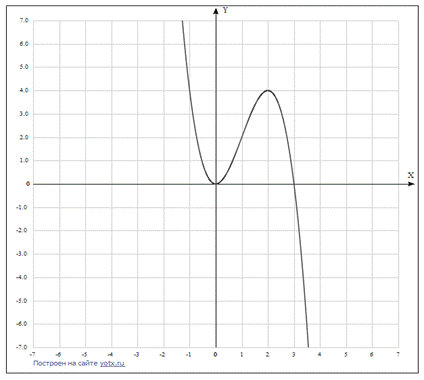
Пример 2. Исследовать функцию 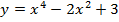и построить ее график.

Решение:

1. .

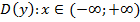2. Имеем: 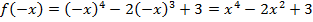. Функция является четной, так как 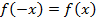. Значит график будет симметричен относительно .

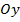3. Найдем точки пересечения графика функции с осями координат.

С осью Ox: 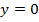, получаем уравнение: 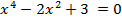. Уравнение является биквадратным, пусть 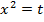, тогда 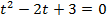. Получившееся уравнение не имеет действительных корней. Значит, точек пересечения графика с осью Ox нет.

С осью Oy: 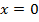, из равенства 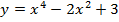получаем 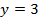. Значит (0;3) 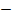точка пересечения с осью Oy.

4. Асимптот нет.

5. а)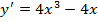

б)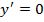

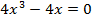
4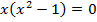

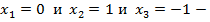критические точки функции

6. Область определения функции разделится на четыре промежутка, определяем знак производной в каждом:

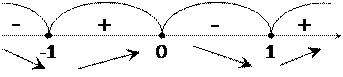При 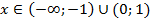функция убывает

При 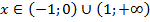функция возрастает

7. Точки экстремум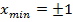а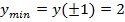: , тогда

, тогда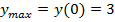

8. а)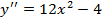

б)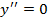

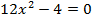
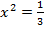
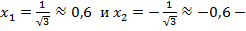критические точки II рода

9. Область определения функции разделится на три промежутка, определяем знак второй производной в каждом:

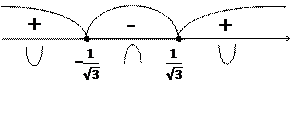При 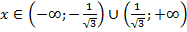функция выпукла вниз

При 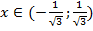функция выпукла вверх

При 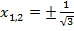имеем точки перегиба, их ординаты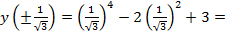

10. Построим график:

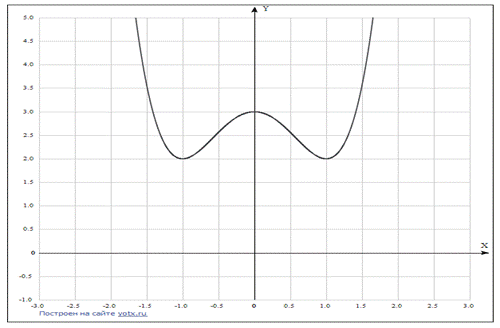
Тема 1.2

Интегральное исчисление функции одной переменной

Неопределенный интеграл

Определение:Функция 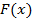, определенная на интервале 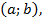называется первообразной для функции 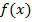, определенной на том же интервале 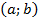, если .

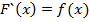Определение:Совокупность всех первообразных 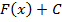функции 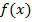на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом 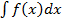, где 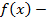подынтегральная функция, 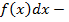подынтегральное выражение, 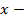переменная интегрирования.

Таким образом, 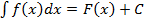, где 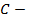любое действительное число.

Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:

.

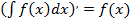Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.