Выбор переменных состояния и формировка уравнений состояния в пространстве состояний

Задание на расчетно-графическую работу

Цельюрасчетно-графической работы является практическое применение метода моделирования для исследования динамики САУ.

Для заданной в виде структурной схемы системы автоматического управления на примере электромеханического привода промышленного манипулятора:

1.Выбрать переменные состояния, сформировать уравнения состояния в пространстве состояний.

2.Получить эквивалентную передаточную функцию системы.

3.Получить фробениусову каноническую форму уравнений состояния.

4.Получить жорданову каноническую форму уравнений состояния.

5.Оценить устойчивость, управляемость, наблюдаемость исследуемой САУ.

6.Получить переходную характеристику с помощью MATLAB.

7.Составить программу расчета переходной характеристики исследуемой САУ.

8.Найти переходную характеристику САУ, оценить параметры системы.

9.Получить графические изображения реакций САУ при одиночных и последовательностях трапецеидального, импульсного и гармонического сигналов.

10.Повторить п.9 при различных числовых параметрах последовательностей сигналов.

11.Сделать анализ-заключение по результатам работы.

Исходные данные для исследования.

a) структурная схема электромеханического привода манипулятора (рис. 1.)

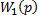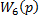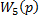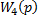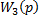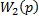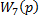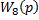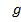
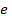
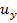
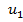
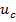
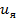
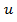
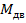
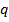
Рис. 1. Структурная схема исследуемой системы.

b) передаточные функции элементов электромеханической системы:

Выбор переменных состояния и формировка уравнений состояния в пространстве состояний.

В любой системе можно выделить совокупность переменных, которые характеризуют динамическую систему. Эти переменные зависят от времени и могут меняться при изменении внешних воздействий на систему. В общем случае, можно выделить некоторую совокупность переменных, которая в полной мере характеризует состояние системы в некоторый момент времени. Такую совокупность переменных называют переменными состояния системы. Она должна быть достаточной для описания различных состояний и режимов системы, но, в то же время, должна быть минимальной и не содержать избыточности. Все элементы исследуемой системы являются элементами первого порядка. Поэтому целесообразно в качестве переменных состояния рассматривать выходные координаты каждого элемента и относительно них сформулировать уравнения для каждого блока.

Таблица 1.

Выходная координата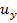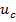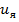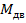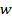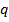
Переменная состояния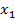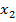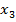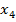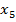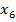

В структурной схеме исследуемой САУ имеется три встречно-параллельных соединения звеньев. Покажем входные координаты звеньев с передаточными функциями 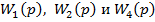через выходные координаты других звеньев.

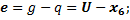
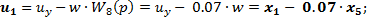
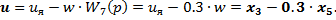
Для получения математической модели системы известны передаточные функции звеньев. Передаточная функция системы (звена) характеризует отношение изображения по Лапласу выходной величины к изображению по Лапласу входной при нулевых начальных условиях:

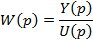
a) Первое уравнение состояния

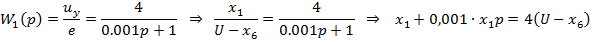
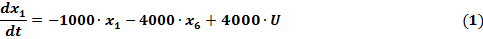
b) Второе уравнение состояния

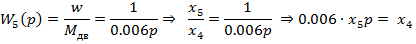
c) Третье уравнение состояния

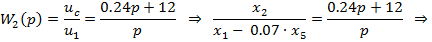
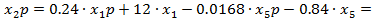
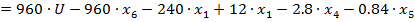
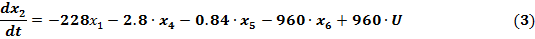
d) Четвертое уравнение состояния

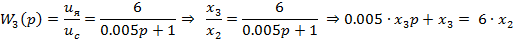
e) Пятое уравнение состояния

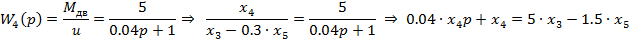
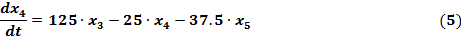
f) Шестое уравнение состояния

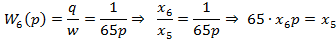
Для непрерывных систем обычно удобнее представлять уравнения состояния (1) – (6) в виде системы в дифференциальной форме. Тогда некоторую непрерывную динамическую систему можно описать с помощью следующей системы уравнений:

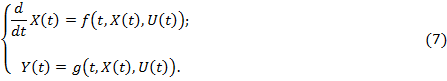
В случае линейности динамических систем равнения (7) можно значительно упростить и записать следующим образом:

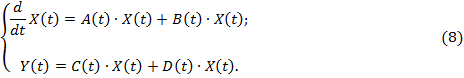
Матрицы коэффициентов 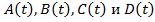определяют структурой и параметрами конкретной динамической системы. Так как исследуемая система стационарная, т.е. ее параметры не зависят от времени, то матрицы коэффициентов постоянны. В этом случае уравнения линейной стационарной динамической системы можно записать в следующем виде:

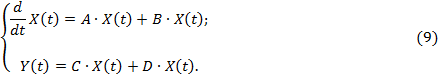
Постоянная квадратная матрица 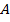, входящая в описание системы, характеризует внутренную структуру системы и ее собственную динамику.

Постоянная квадратная матрица 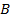характеризует структуру входного устройства системы, а постоянная матрица 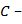структуру выходного устройства системы.

Постоянная матрица 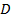связывает вектор входа и вектор выхода системы.

Таким образом, математическая модель исследуемой САУ в пространстве состояний будет иметь следующий вид:

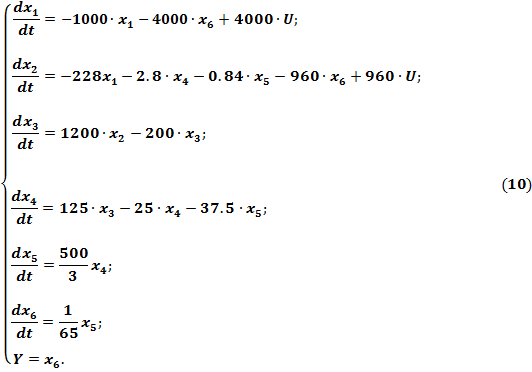
Здесь первые пять уравнений являются уравнениями состояния системы, а последнее уравнение – это уравнение выхода системы.

Используя формулу (9), запишем математическую модель исследуемой САУ в пространстве состояний в векторно-матричной форме:

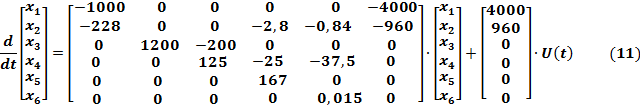
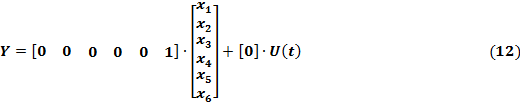
Таким образом, в пространстве состояний исследуемая система описывается системой из шести дифференциальных уравнений первого порядка и одним линейным алгебраическим уравнением.

Запишем отдельно матрицы коэффициентов.

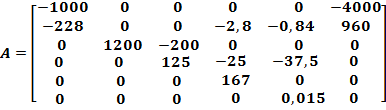– матрица состояний системы.

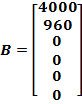– входная матрица системы.

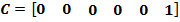– выходная матрица системы.

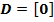– вход-выходная матрица системы.

Уравнениям (11) и (12) соответствует следующая блок-схема:

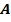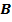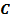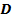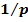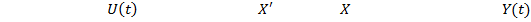
Рис. 2. Реализация линейной системы в пространстве состояний.