Дифференциальное исчисление функции одной переменной

1. Определение производной. Дифференцируемая функция и ее дифференциал.

2. Связь между непрерывностью и дифференцируемостью. Правила дифференцирования суммы, произведения, частного.

3. Дифференцирование сложной функции. Логарифмическое дифференцирование. Дифференцирование обратной функции, параметрически заданной функции. Таблица производных.

4. Производные и дифференциалы высших порядков. Инвариантность формы дифференциала.

5. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя для раскрытия неопределенностей вида 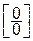или 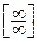. Использование правила Лопиталя при вычислении пределов для раскрытия неопределенностей вида , , , .

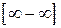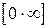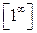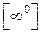6. Формула Тейлора с остаточным членом в форме Пеано и Лагранжа. Формула Маклорена для основных элементарных функций.

7. Признаки возрастания и убывания функции на промежутке. Локальный экстремум функции. Необходимое условие экстремума; достаточные условия экстремума. Наибольшее и наименьшее значения функции на отрезке.

8. Определение выпуклой кривой, вогнутой кривой, точки перегиба. Условия выпуклости и вогнутости кривой. Понятие асимптоты кривой, отыскание вертикальных и невертикальных асимптот. Общая схема исследования функции и построение её графика.

9. Понятие функции нескольких переменных. Предел и непрерывность функции. Определение и вычисление частных производных.

Номера контрольных работ, которые необходимо выполнить в первом семестре, и номера задач соответствующих вариантов представлены в табл. 1.

Таблица 1

Номер варианта	Контрольная работа № 1 Номера задач	Контрольная работа № 2 Номера задач
	1 11 21 31	41 51 61 71
	2 12 22 32	42 52 62 72
	3 13 23 33	43 53 63 73
	4 14 24 34	44 54 64 74
	5 15 25 35	45 55 65 75
	6 16 26 36	46 56 66 76
	7 17 27 37	47 57 67 77
	8 18 28 38	48 58 68 78
	9 19 29 39	49 59 69 79
	10 20 30 40	50 60 70 80

II семестр

Программа

Интегральное исчисление функции одной переменной

1. Первообразная функции и её свойства. Понятие неопределенного интеграла, его свойства. Таблица основных интегралов.

2. Основные методы интегрирования: метод подведения под знак дифференциала, метод замены переменной, метод интегрирования по частям.

3. Интегрирование некоторых классов функций: тригонометрических функций; функций, содержащих квадратный трехчлен; дробно-рациональных функций.

4. Понятие определенного интеграла, его свойства. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Приложения определенных интегралов: вычисление площади плоской фигуры, длины дуги кривой, объема тела вращения.

5. Несобственные интегралы первого и второго рода, их вычисление.