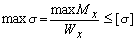Определение деформаций и перемещений

Определим упругие деформации стержня предполагая, что изменение его длины при растяжении Dl, называемое абсолютной продольной деформацией или удлинением, мало по сравнению с его первоначальной длиной l(Dl<<l). Тогда относительная продольная деформация будет равна

e = Dl / l

Учитывая, что согласно закону Гука для одноосного растяжения (сжатия)

e = s / E

где Е - модуль продольной упругости материала стержня, а нормальные напряжения определяются по формуле -s=N_z /F (в нашем случае N_z=P), для абсолютной деформации получаем

Dl = N_z / EF

(2)

Произведение EF принято называть жесткостью поперечного сечения стержня при растяжении (сжатии), так как удлинение обратно пропорционально EF.

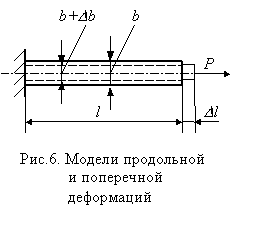Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются (см. рис. 6), а при сжатии - увеличиваются. Это явление получило название эффекта Пуассона.

По аналогии с продольной деформацией изменение размеров поперечного сечения Db (на рис. 6 Db<0) будем называть абсолютной поперечной деформацией, а e'=Db/b - относительной поперечной деформацией. Относительные продольная и поперечная деформа-ции, имеющие противоположные знаки, связаны между собой коэффициентом m, являющимся константой материала и называемым коэффициентом поперечной деформации или коэффициентом Пуассона:

e' = - me

Как известно, для изотропного материала 0 £ m £1/2.

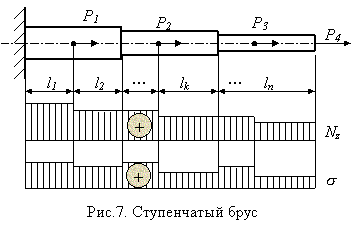
Формула (2) для удлинения стержня Dl применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EF=const, N_z=const). Удлинение стержня со ступенчатым изменением EF и N_z (рис. 7) может быть определено как сумма удлинений ступеней, у которых EF и N_z постоянны:

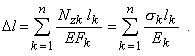
(индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов). В случае, когда N_z и EF меняются по длине стержня l непрерывно и их можно считать постоянными лишь в пределах ступеней длиной dz, обобщая формулу эту, получаем

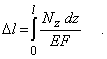
В качестве тестов для практики расчетов определенных интегралов рекомендую воспользоваться системой входных тестов Т-5, указанных в ПРИЛОЖЕНИИ.

С упругими продольными деформациями стержня при растяжении (сжатии) связаны продольные перемещения его сечений. На рис. 8 приведены три случая определения таких перемещений, откуда видно, что перемещения поперечных сечений численно равны удлинениям заштрихованных частей стержня:

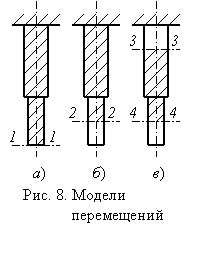• перемещение свободного торцевого сечения 1-1 при неподвижном другом торцевом сечении (рис. 8, а) численно равно удлинению стержня;
• перемещение промежуточного сечения 2-2 (рис. 8, б) численно равно удлинению части стержня, заключенной между данным сечением и сечением неподвижным;
• взаимное перемещение сечений 3-3 и 4-4 (рис, 8, в) численно равно удлинению части стержня, заключенной между этими сечениями.

Напряженное состояние при растяжении (сжатии)

Напряженное состояние при растяжении стержня является одноосным (рис. 9, а). Поскольку на поперечных и продольных площадках касательные напряжения не возникают, то эти площадки являются главными. Причем в случае растяжения s₁ =s >0, s₂=s₃=0, а в случае сжатия s₁=s₂=0, а s₃=s<0.

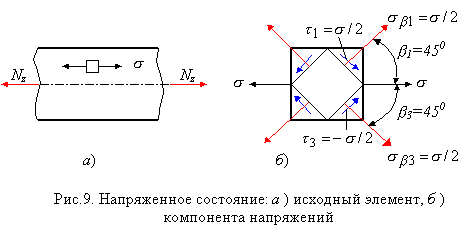
Напряжения на площадках, наклоненных к оси стержня под углом a, определяются по формулам для упрощенного плоского напряженного состояния:

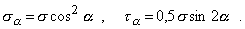
Площадки с экстремальными касательными напряжениями t₁₃ (рис. 9, б), как известно, наклонены по отношению к исходным под углами b=±45° (следует и из формулы для t_a) и равны t₁₃=s/2.

Именно с действием экстремальных t связывается появление на боковой поверхности образца из малоуглеродистой стали, испытываемого на растяжение, линий скольжения, ориентированных под углом b=±45° к оси образца. На площадках с экстремальными t действуют и нормальные напряжения, равные s₁₃=s/2.

13 Прямой чистый изгиб призматического стержня

Ключевые слова: прочность, жесткость, осевой момент инерции, осевой момент сопротивления.

При прямом чистом изгибе в поперечном сечении стержня возникает только один силовой фактор - изгибающий момент М_х (рис. 1). Так как Q_y=dM_x/dz=0, то M_x=const и чистый прямой изгиб может быть реализован при загружении стержня парами сил, приложенными в торцевых сечениях стержня. Поскольку изгибающий момент M_х по определению равен сумме моментов внутренних сил относительно оси Ох с нормальными напряжениями его связывает выкающее из этого определения уравнение статики

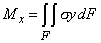
Сформулируем предпосылки теории чистого прямого изгиба призматического стержня. Для этого проанализируем деформации модели стержня из низкомодульного материала, на боковой поверхности которого нанесена сетка продольных и поперечных рисок (рис. 2). Поскольку поперечные риски при изгибе стержня парами сил, приложенными в торцевых сечениях, остаются прямыми и перпендикулярными к искривленным продольным рискам, это позволяет сделать вывод о выполнении гипотезы плоских сечений, которая, как показывает решение этой задачи методами теории упругости, перестает быть гипотезой, становясь точным фактом - законом плоских сечений. Замеряя изменение расстояний между продольными рисками, приходим к выводу о справедливости гипотезы о ненадавливании продольных волокон (s_х =s_y=0).

Ортогональность продольных и поперечных рисок до и после деформирования (как отражение действия закона плоских сечений) указывает также на отсутствие сдвигов, касательных напряжений в поперечных и продольных сечениях стержня.

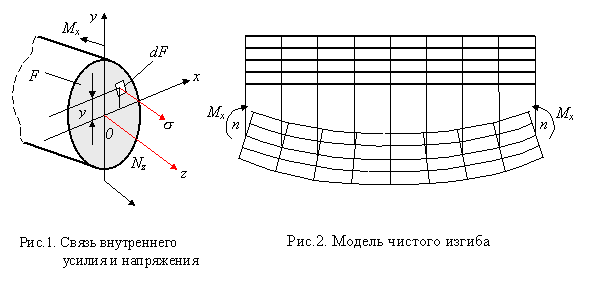
Таким образом, чистый прямой изгиб призматического стержня сводится к одноосному растяжению или сжатию продольных волокон напряжениями s (индекс г в дальнейшем опускаем). При этом часть волокон находится в зоне растяжения (на рис. 2 это - нижние волокна), а другая часть - в зоне сжатия (верхние волокна). Эти зоны разделены нейтральным слоем (n-n), не меняющим своей длины, напряжения в котором равны нулю. Учитывая сформулированные выше предпосылки и полагая, что материал стержня линейно-упругий, т. е. закон Гука в этом случае имеет вид: s=eЕ, выведем формулы для кривизны нейтрального слоя 1/r (r - радиус кривизны) и нормальных напряжений s. Предварительно отметим, что постоянство поперечного сечения призматического стержня и изгибающего момента (M_х=сonst), обеспечивает постоянство радиуса кривизны нейтрального слоя по длине стержня (рис. 3, а), нейтральный слой (n-n) описывается дугой окружности.

Рассмотрим призматический стержень в условиях прямого чистого изгиба (рис. 3, а) с поперечным сечением, симметричным относительно вертикальной оси Оу. Это условие не отразится на конечном результате (чтобы прямой изгиб был возможен, необходимо совпадение оси Оу с главной осью инерции поперечного сечения, которая и является осью симметрии). Ось Ox поместим на нейтральном слое, положение которого заранее неизвестно.

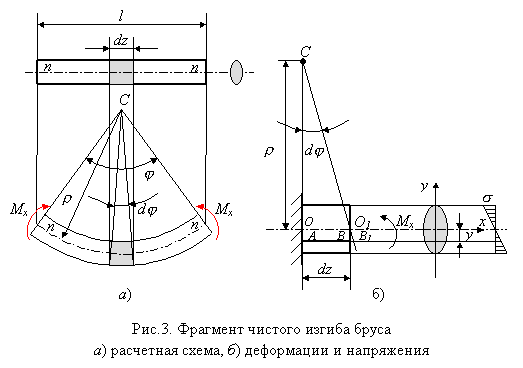
Рассмотрим вырезанный из стержня элемент длиной dz, который в масштабе с искаженными в интересах наглядности пропорциями изображен на рис. 3, б. Поскольку интерес представляют деформации элемента, определяемые относительным смещением его точек, одно из торцевых сечений элемента можно считать неподвижным. Ввиду малости dj считаем, что точки поперечного сечения при повороте на этот угол перемещаются не по дугам, а по соответствующим касательным.

Вычислим относительную деформацию продольного волокна АВ, отстоящего от нейтрального слоя на у:

e =ВВ₁ / АВ=ВВ₁ / ОО₁

Из подобия треугольников С00₁ и 0₁ВВ₁ следует, что

BB₁ / OO₁ = O₁B/CO = y /r

Продольная деформация e оказалась линейной функцией расстояния от нейтрального слоя, что является прямым следствием закона плоских сечений

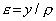
(1)

Тогда нормальное напряжение, растягивающее волокно АВ, на основании закона Гука будет равно

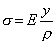
(2)

Эта формула не пригодна для практического использования, так как содержит две неизвестные: кривизну нейтрального слоя 1/r и положение нейтральной оси Ох, от которой отсчитывается координата у. Для определения этих неизвестных воспользуемся уравнениями равновесия статики. Первое выражает требование равенства нулю продольной силы

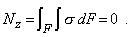
(3)

Подставляя в это уравнение выражение (2)

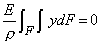
и учитывая, что (Е / r) ¹ 0, получаем, что

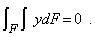
Интеграл в левой части этого уравнения представляет собой статический момент поперечного сечения стержня относительно нейтральной оси Ох, который может быть равным нулю только относительно центральной оси. Поэтому нейтральная ось Ох проходит через центр тяжести поперечного сечения.

Вторым уравнением равновесия статики является, связывающее нормальные напряжения с изгибающим моментом (который легко может быть выражен через внешние силы и поэтому считается заданной величиной). Подставляя в уравнение связки выражение для. напряжений, получим:

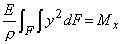
и учитывая, что 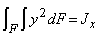где J_x - главный центральный момент инерции относительно оси Ох, для кривизны нейтрального слоя получаем формулу

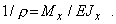
(4)

Кривизна нейтрального слоя 1/s является мерой деформации стержня при прямом чистом изгибе. 1/s тем меньше, чем больше величина EJ_х, называемая жесткостью поперечного сечения при изгибе (по аналогии с жесткостью поперечного сечения при растяжении EF).

Подставляя (4) в (2), получаем формулу для нормальных напряжений в виде

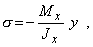
(5)

которая была впервые получена Ш. Кулоном в 1773 году. Для согласования знаков изгибающего момента М_х и нормальных напряжений s в правой части формулы (5) ставится знак минус, 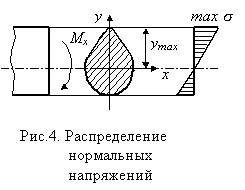так как при M_х>0 нормальные напряжения s при y>0 оказываются сжимающими. Однако в практических расчетах удобнее, не придерживаясь формального правила знаков, определять напряжения по модулю, а знак ставить по смыслу. Нормальные напряжения при чистом изгибе призматического стержня являются линейной функцией координаты у и достигают наибольших значений в волокнах, наиболее удаленных от нейтральной оси (рис. 4), т. е.

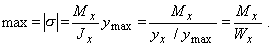
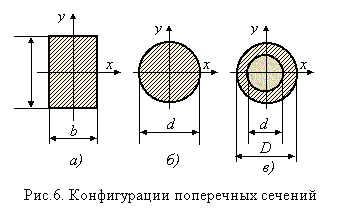
Здесь введена геометрическая характеристика 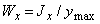, имеющая размерность м³ и получившая название момента сопротивления при изгибе. Поскольку при заданном M_х напряжения max s тем меньше, чем больше W_x, момент сопротивления является геометрической характеристикой прочности поперечного сечения изгибе. Приведем примеры вычисления моментов сопротивления для простейших форм поперечных сечений. Для прямоугольного поперечного сечения (рис. 5, а) имеем J_х=bh³/12, y_max = h/2 и W_x = J_x/y_max = bh²/6. Аналогично для круга (рис. 5,6 J_x=pd⁴/64, y_max=d/2) получаем W_x=pd³/32, для кругового кольцевого сечения (рис. 5, в), у которого

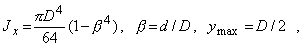
получаем

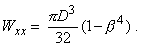
Итак, максимальные нормальные напряжения в сечении с изгибающим моментом M_х определяются по формуле

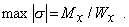
(6)

Этой формулой удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня получает вид

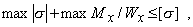
где max M_х - максимальное значение изгибающего момента (легко определяемое по его эпюре), [s] - допускаемое напряжение на простое растяжение (сжатие). Напомним, 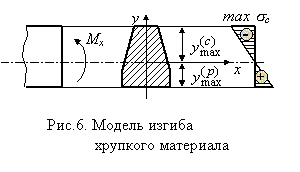что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором s=const).

При расчете балок из хрупких материалов следует различать наибольшие растягивающие max s_p и наибольшие сжимающие max |s_c| напряжения (рис. 6), которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение |s_т| и сжатие [s_с]. Условие прочности в этом случае будет иметь вид:

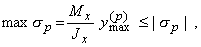
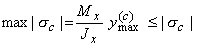
14 Прямой поперечный изгиб призматического стержня

Ключевые слова: прочность, жесткость, двутавр, швеллер, рациональное сечение, равнопрочность.

При прямом поперечном изгибе в сечениях стержня возникает изгибающий момент М_х и поперечная сила Q_y (рис. 1), которые связаны с нормальными s и касательными t_yz напряжениями

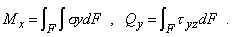
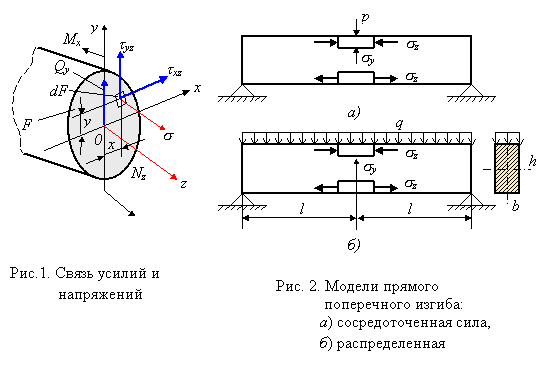
Выведенная в случае чистого изгиба стержня формула для прямого поперечного изгиба, вообще говоря, неприменима, поскольку из-за сдвигов, вызываемых касательными напряжениями t_yz, происходит депланация поперечных сечении (отклонение от закона плоских сечений). Однако для балок с высотой сечения h<l/4 (рис. 2) погрешность невелика и ее применяют для определения нормальных напряжений поперечного изгиба как приближенную. При выводе условия прочности при чистом изгибе использовалась гипотеза об отсутствии поперечного взаимодействия продольных волокон. При поперечном изгибе наблюдаются отклонения от этой гипотезы:

а) в местах приложения сосредоточенных сил. Под сосредоточенной силой напряжения поперечного взаимодействия могут быть достаточно велики и во много раз превышать продольные напряжения s_z, убывая при этом, в соответствии с принципом Сен-Венана, по мере удаления от точки приложения силы;

б) в местах приложения распределенных нагрузок. Так, в случае, приведенном на рис. 2, б, напряжения от давления на верхние волокна балки sy = -q/b. Сравнивая их с продольными напряжениями s_z, имеющими порядок

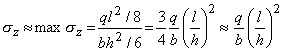
приходим к выводу, что напряжения s_y << s_z при условии, что h² << l², так как s_y /s_z 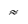(h/l)² << 1.

Получим формулу для касательных напряжений t_yz. Примем, методика расчета нормальных напряжений известна, что касательные напряжения равномерно распределены по ширине поперечного сечения (рис. 3). Эта предпосылка выполняется тем точнее, чем уже поперечное сечение стержня. Точное решение задачи для прямоугольного поперечного сечения показывает, что отклонение от равномерного распределения tyz , зависит от отношения сторон b/h. При (b/h)=1,0 оно составляет 12,6%, при (b/h)=0,5 - только 3,3%.

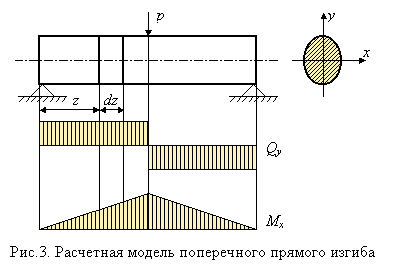
Непосредственное определение напряжений t_yz затруднительно, поэтому находим равные им (вследствие закона парности) касательные напряжения t_yz, возникающие на продольной площадке с координатой у элемента длиной dz, вырезанного из балки, (рис. 3). Сам элемент показан на рис. 4. От этого элемента продольным сечением, отстоящим от нейтрального слоя на у, отсекаем верхнюю часть, заменяя действие отброшенной нижней части касательными напряжениями t (индекс гу в дальнейшем опускаем), равнодействующая которых dT=tbdz показана на рис. 5. Здесь, согласно второй предпосылке

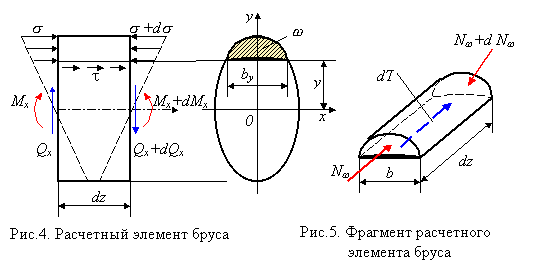
t=const по ширине элемента b. Нормальные напряжения s и s + ds, действующие на торцевых площадках элемента, также заменим их равнодействующими

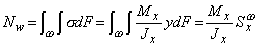
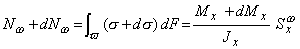
Согласно первой предпосылке нормальные напряжения определяются уже известным способом, 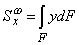, где S_x^w - статический момент отсеченной части площади поперечного сечения w относительно оси Ох.

Рассмотрим условие равновесия элемента (рис. 5) составив для него уравнение статики Sz = 0:

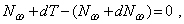
откуда после несложных преобразований, учитывая, что

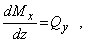
получаем формулу для касательных напряжений при нормальном поперечном изгибе призматического стержня

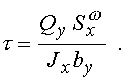
которая называется формулой Журавского. В этой формуле b_y - ширина сечения в том месте, где определяются касательные напряжения, а статический момент, подставляемый в эту формулу, может быть вычислен как для верхней, так и для нижней части (статические моменты этих частей сечения относительно его центральной оси Ох отличаются только знаком, так как статическим момент всего сечения равен нулю).

В качестве примера применения формулы Журавского построим эпюру касательных напряжений для случая прямоугольного поперечного сечения балки (рис. 6). Учитывая, что для этого сечения

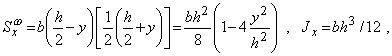
получаем

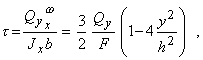
где F=bh - площадь прямоугольника.

Как видно из формулы, касательные напряжения по высоте сечения меняются по закону квадратичеокой параболы, достигая максимума на нейтральной оси

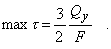
Сделаем несколько замечаний, касающихся расчетов на прочность при прямом поперечном изгибе. В отличие от простых видов деформации, когда в поперечных сечениях стержня возникает лишь один силовой фактор, к которым относятся и изученные выше растяжение (сжатие) и чистый изгиб, прямой поперечный изгиб должен быть отнесен к сложным видам деформации. В поперечных сечениях стержня при поперечном изгибе возникают два силовых фактора: изгибающий момент М_х и поперечная сила Q_y (рис. 7), напряженное состояние является упрощенным плоским, при котором в окрестности произвольно выбранных точек поперечного сечения действуют нормальные s и касательные t напряжения. Поэтому условие прочности для таких точек должно быть сформулировано на основе какого-либо уже известного критерия прочности.

Однако учитывая, что наибольшие нормальные напряжения возникают в крайних волокнах, где касательные напряжения отсутствуют (рис. 7), а наибольшие касательные напряжения во многих случаях имеют место в нейтральном слое, где нормальные напряжения равны нулю, условия прочности в этих случаях формулируются раздельно по нормальным и касательным напряжениям

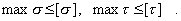
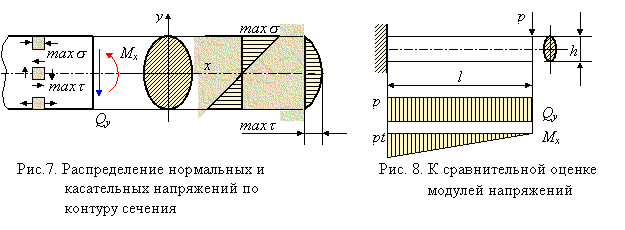
Покажем, что доминирующая роль в расчетах на прочность балки, подвергнутой поперечному изгибу, будет принадлежать расчету по нормальным напряжениям. Для этого оценим порядок max s и max t на примере консольной балки, показанной на рис. 8:

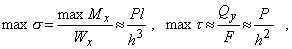
так как 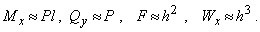Тогда

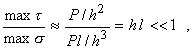
откуда max t<<maxs, а поскольку [t]/[s] 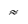0,5 то доминирующим в этом случае будет расчет по нормальным напряжениям и условие прочности, например, для балки из пластичного материала, работающей на прямой изгиб, как и в случае чистого изгиба будет иметь вид