Формула интегрирования по частям и формула – это два взаимно обратных правила

Пример 2

Найти неопределенный интеграл.

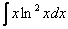
Подынтегральная функция представляет собой произведение логарифма на многочлен.
Решаем.

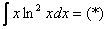
Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.

Как уже говорилось, за 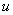необходимо обозначить логарифм (то, что он в степени – значения не имеет). За 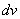обозначаем оставшуюся часть подынтегрального выражения.

Записываем в столбик:

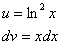
Сначала находим дифференциал :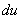

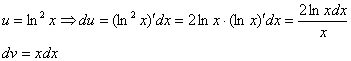
Здесь использовано правило дифференцирования сложной функции 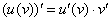. Не случайно, на самом первом уроке темы Неопределенный интеграл. Примеры решений я акцентировал внимание на том, что для того, чтобы освоить интегралы, необходимо «набить руку» на производных. С производными придется столкнуться еще не раз.

Теперь находим функцию 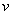, для этого интегрируем правую часть нижнего равенства :

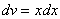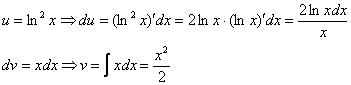
Для интегрирования мы применили простейшую табличную формулу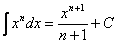

Теперь всё готово для применения формулы 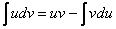. Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью :

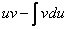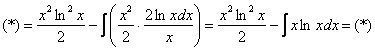
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за 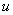в похожих ситуациях всегда обозначается логарифм.

Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.

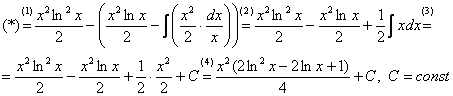
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей скобке 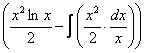, и эти скобки нужно корректно раскрыть.

(2) Раскрываем скобки. Последний интеграл упрощаем.

(3) Берем последний интеграл.

(4) «Причесываем» ответ.

Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.

А сейчас пара примеров для самостоятельного решения:

Пример 3

Найти неопределенный интеграл.

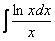
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.

Пример 4

Найти неопределенный интеграл.

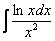
А вот этот интеграл интегрируется по частям (обещанная дробь).

Это примеры для самостоятельного решения, решения и ответы в конце урока.

Вроде бы в примерах 3,4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.

По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочлена четвертой степени и т.д. Нет, презерватив на глобус я натягивать не буду, но вы все прочитаете мой пост Графики и свойства элементарных функций =).