Измерения неравноточные

При неравнорассеянных результатах измерения в группах их объединение осуществляется таким образом, чтобы получить наиболее эффективную оценку математического ожидания 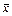. Эту оценку будем искать, используя принцип максимального правдоподобия (пп. 2.3.1).

Если средние арифметические в группах можно считать распределенными по нормальному закону, то функцию правдоподобия можно представить в виде

. (3.15)

Логарифмическая функция правдоподобия

. (3.16)

Нам нужно найти эффективную оценку , поэтому приравниваем нулю производную по

.

Отсюда

. (3.17)

Это так называемое средневзвешенное, которое принимается за оценку математического ожидания объединенных групп.

Для равных дисперсий получаем выражение (3.12).

Оценка дисперсии

. (3.18)

После получения оценок дисперсии вычисляют границы случайной погрешности по формуле (3.3), в которой t_P для (n₁₊ n₂) > 30 , берется для нормального распределения.