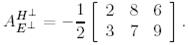Түйіндес кеңістіктегі ортогональ толықтауыш

Анықтама 5. Айталық 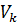- 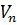векторлық кеңістіктің кез келген ішкі кеңістігі болсын. 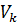-ға тиісті барлық векторларға ортогональ 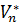-ға тиісті ковекторлардың жиынын 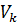кеңістігіне ортогональ толықтауыш деп атайды және оны 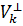деп белгілейді:

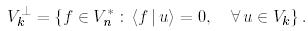
Басқаша айтқанда, 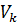кеңістігіне ортогональ толықтауыш - бұл , 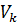-ға тиісті векторларда нөлге айналатын, 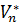-ға тиісті барлық сызықтық функциялардың жиыны.

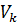ішкі кеңістігінің ортогональ толықтауышы басқа 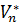кеңістігінде жатады.

Теорема 2. 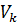ішкі кеңістігінің ортогональ толықтауышы 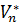кеңістігінің ішкі кеңістігі болып табылады, сонымен қатар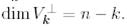

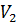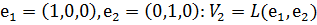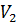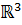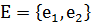Мысал 3. (Ішкі кеңістікке ортогонал толықтауыш). -де векторлар жүйесін қарастырайық, олар векторларына созылған сызықтық қабықша болып табылады. - -те базисі бар ішкі кеңістік. 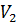-ге 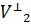ортогональ толықтауыш

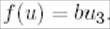(18)

түріндегі сызықтық функциялар жиыны болатындығын көрсетейік.

Расында да, кез келген 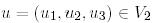векторы 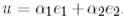түріне келтірімді. (18) түрдегі 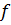функциясы үшін 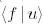есептейік:

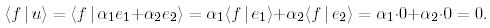
Осылайша, (18) түрдегі кез келген функция 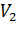ішкі кеңістігінің базисіне ортогональді, ендеше осы ішкі кеңістіктің кез келген векторына да ортогональ болады, дәлелдеу керегі де осы еді.

Мысал 4. (ортогональ толықтауыш және оның өлшемі). Берілген 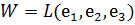ішкі кеңістігі үшін 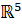векторлық кеңістігінің 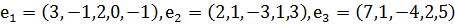векторларына созылған сызықтық қабықшаның 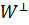ортогональ толықтауышын құрайық. 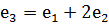болғандықтан, онда 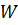базисі ретінде 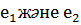векторларын алуға болады. Бұдан 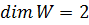, ендеше .

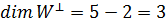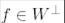функциясының түрін анықтау үшін

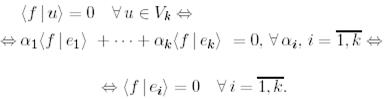
тепе-теңдігін қолданайық.

Айталық 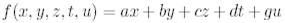- -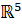те әрекет ететін кез келген сызықтық функция болсын. 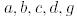параметрлерінің қандай мәнінде 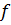функциясы 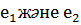векторларына ортогонал болатындығын анықтайық. 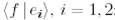жүйесін шешейік:

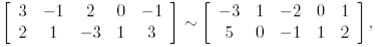
бұдан

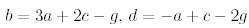
аламыз. Осылайша,

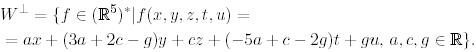
Базис ретінде келесі функцияларды алуға болады:

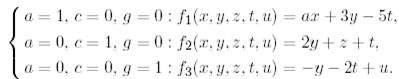
Түйіндес бейнелеу

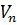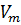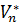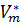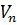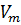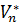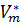және екі сызықтық кеңістігін, сонымен қатар оған түйіндес және кеңістіктерін қарастырайық. Енді және кеңістіктерінің, сонымен қатар және кеңістіктерінің бейнелеуін қарастырып, осы бейнелеулер арасында өзара бірмәнді сәйкестік болатындығын орнатайық.

Айталық қандай да бір 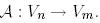сызықтық бейнелеуі берілсін.

Анықтама 6. 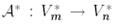бейнелеуі 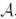үшін түйіндес бейнелеу деп аталады, егер кез келген 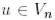және кез келген 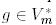үшін төмендегі қатынас орындалса:

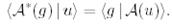(19)

Теорема 3. Кез келген берілген 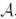сызықтық бейнелеуі үшін 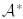түйіндес бейнелеуі бар, сызықты және жалғыз болады.

Мысал 5. (Түйіндес бейнелеу).

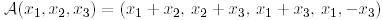
болатындай 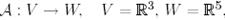бейнелеуі және 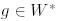ковекторы үшін

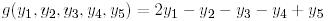
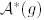түйіндес бейнелеуі кезіндегі оның 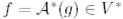бейнесін табайық:

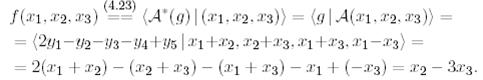
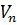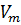Айталық, және кеңістіктерінен 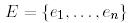және 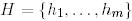базистері таңдап алынсын. Бұл базистарға 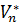және 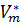түйіндес кеңістіктердің 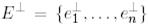және 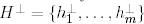биортогональды базистері сәйкес келеді.

Айталық 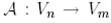сызықтық бейнелеуі және оған түйіндес 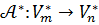бейнелеуі берілсін.

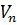сызықтық кеңістіктің әрбір Е, Н базистер жұбы және 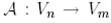сызықтық бейнелеуі осы бейнелеудің матрицасымен байланысты. Берілген базистегі сызықтық бейнелеудің матрицасы деп 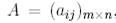матрицасын айтады, мұнда j-шы баған 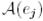векторының координатынан құралған, яғни Н базисінде j-шы базистік вектордың бейнесінің координаты болып табылады:

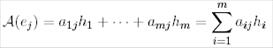
Берілген матрица мен түйіндес бейнелеудің арасындағы байланысты зерттейік.

Айталық, Е,Н базисіндегі 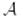бейнелеуі 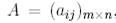матрицасына ие болсын. 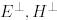биортогональ базистеріндегі 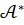түйіндес бейнелеудің 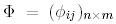матрицасының құрылымын анықтайық.

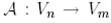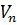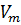Теорема 4. Айталық сызықтық бейнелеу, Е және Н – сәйкесінше және кеңістіктерінің базистері, 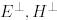- 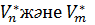кеңістіктерінің биортогональ базистері болсын. Онда егер 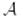бейнелеуі Е және Н базистерінде А матрицасына ие болса, онда 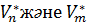биортогональ базистерінде 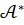түйіндес бейнелеуі 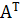матрицасына ие болады.

Дәлелдеуі. А және 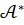бейнелеулерінің матрицасының анықтама бойынша келесі жіктелуден анықталады:

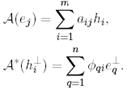(20)

(19) түйіндес бейнелеудің анықталатын қатынасынан мынаны аламыз:

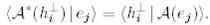(21)

Бұл теңдіктің оң жақ және сол жақ бөліктерін жеке – жеке (20) қолданып есептейік:

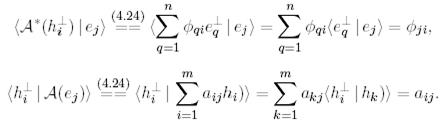
Алынған өрнектерді (21) қойып, 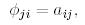болатындығын аламыз, ал бұл 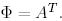дегенді білдіреді.

Мысал 6. (Түйіндес бейнелеудің матрицасы).

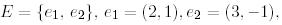(22)

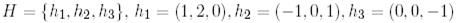
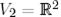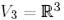базистерімен берілген және екі сызықтық кеңістікті және 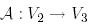сызықтық бейнелеуін қарастырайық:

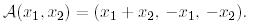
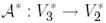түйіндес бейнелеудің 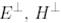биортогональ базистегі матрицасын табайық.

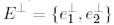биортогональ базисін 1-мысалға сәйкес анықтайық. 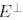биортогональ базисін анықтау үшін жүйені шешеміз:

.

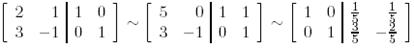Бұдан 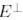мынадай ковекторлардан тұрады:

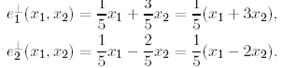(23)

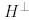табу үшін жүйені шешеміз:

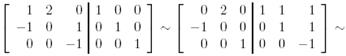
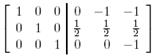
Бұдан 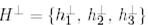төмендегідей ковекторлардан құралады:

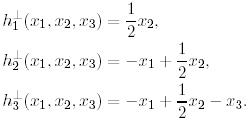(24)

Е және Н базисіндегі 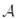бейнелеуінің 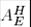матрицасын табайық. Ол үшін Е базисінің 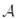бейнелеуіндегі базистік векторларының бейнесін есептейік:

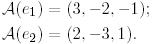
Н базисіндегі ізделінді 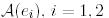векторының координаттық бағанын 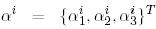деп белгілейік:

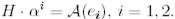(25)

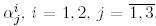координатын табайық. Ол үшін (25) теңдікті 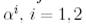қатысты шешеміз:

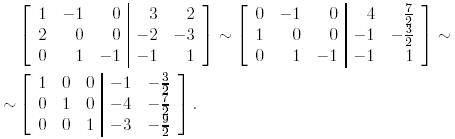
Осылайша, Е және Н базисіндегі 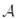бейнелеуінің матрицасы мына түрге ие болады:

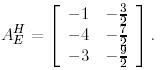
Ендеше 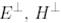базистеріндегі 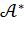түйіндес бейнелеудің 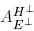матрицасы мына түрге ие болады: