Тең жартыға бөлу әдісі . Есептің қойылыуы

Есептің қойылыуы. Теңдеудің түбірін табу математикалық мәселесі ғылым мен техниканың әртүрлі салаларында жиі кездеседі. Бізге келесі теңдеулердің түбірлерін табу керек болсын:

(4.1)

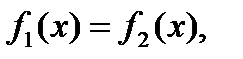немесе (4.2)

мұндағы 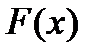және 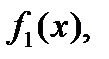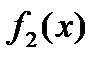- кейбір 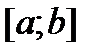аралығында анықталған, үзіліссіз және дифференциялданатын функциялар.

Бұл теңдеулерді

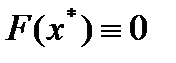(4.1а)

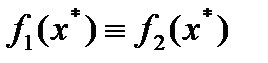(4.2а)

түріндегі тепе-теңдікке айналдыратын 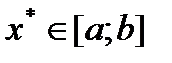саны теңдеудің түбірі немесе теңдеудің шешімі деп аталады. Егер 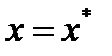кезінде 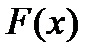функциясымен бірге оның 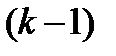-ші ретке дейінгі туындыларының барлығы нольге тең болса, онда мұндай 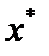саны k еселі түбір деп аталады:

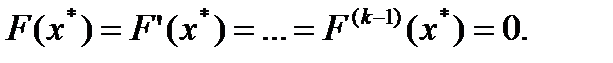
Бір еселі түбір жай деп аталады. Егер (4.1) теңдеудің сол жағы тек ғана алгебралық функциялар (бүтін, рационал, ироционал) болса, онда (4.1) теңдеу алгебралық деп аталады.

Мысалы: 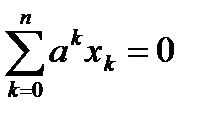- бүтін алгебралық функция.

Ал егер (4.1) теңдеудің сол жағы алгебралық функция болмаса (логорифмдік, көрсеткіштік, тригонометриялық және т.б), онда ол трансценденттік деп аталады.

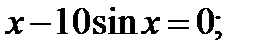
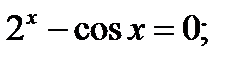
Мысалы: 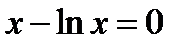т.б.

Сызықты емес теңдеулерді шешудің тура және итерациялық әдістері бар. Теңдеуді шешудің тура әдістері оның шешімін белгілі бір текті қатынастар (формулалар) арқылы өрнектейді. Мысалы, алгебра курсынан тригонометриялық, көрсеткіштік, логарифмдік, алгебралық екінші дәрежелі 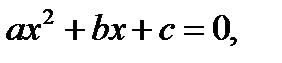толымсыз үшінші дәрежелі 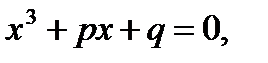биквадрат 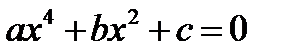теңдеулерінің түбірлерінің формулалары белгілі. Әрине, практикада кездесетін теңдеулерді мұндай қарапайым әдістермен шеше беруге мүмкін бола бермейді. Сондықтан қандай да бір сандық әдісті пайдалану қажеттілігі туады: (4.1) немесе (4.2) теңдеуінің [а;b] аралығында берілген e дәлдікпен барлық нақты түбірлерін табу керек. Мұндай кезде теңдеудің түбірлерін табу үшін негізінен екі: бөліктеу (айыру) және дәлелдеу кезеңінен тұратын итерациялық немесе біртіндеп жуықтау әдістерін қолданамыз.

Билеті №5

Бір айнымалы функциялар.

1) Бір айнымалы функциялар. Аргументтің жеткілікті аз 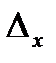қателігінен пайда болған дифференциялданатын 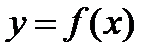функциясының абсолют қателігі

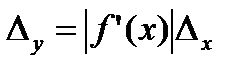(3.1)

шамасымен бағаланады.

Егер 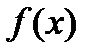функциясының мәндері оң болса, онда салыстырмалы қателік үшін келесі бағалау орынды:

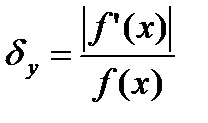
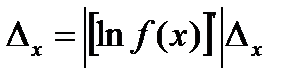
(3.2)

Дербес жағдайда негізгі элементар функциялар үшін келесідей ережелерді аламыз:

а) 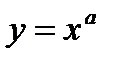дәрежелі функциясы. Дәрежелі функцияның абсолют қателігі былайша анықталады:

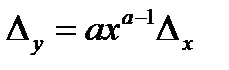(3.3)

Дәрежелі функцияның салыстырмалы қателігі:

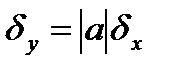(3.4)

б) 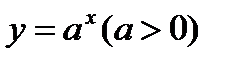көрсеткішті функциясы. Көрсеткішті функцияның абсолют қателігі:

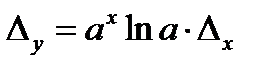(3.5)

Ал салыстырмалы қателігі:

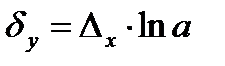(3.6)

Дербес жағдайда 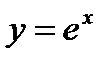функциясыүшін

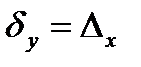(3.7)

екеніне көз жеткіземіз.

в) 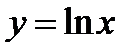логорифмдік функциясы. Санның натурал логарифмнің абсолют қателігі санның өзінің салыстырмалы қателігіне тең:

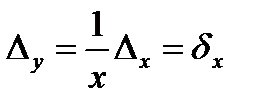(3.8)

г) Тригонометриялық функциялар. Синус пен косинустың абсолют қателіктері аргументтің абсолют қателіктерінен аспайды:

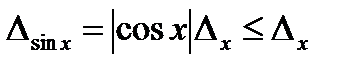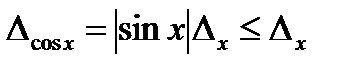, (3.9)

Тангенс пен котангенстің абсолют қателіктері барлық уақытта аргументтің қателігінен үлкен:

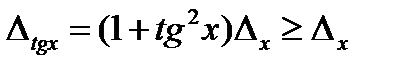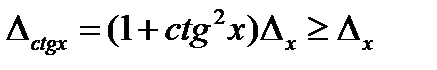, (3.10)