С использованием нечеткой логики

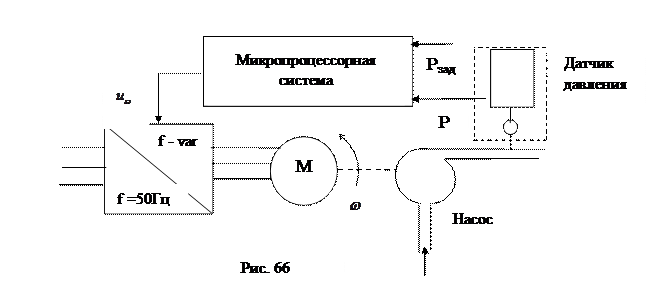
Пример 10.Рассмотрим пример управления асинхронным электроприводом центробежного насоса для стабилизации давления в системе водоснабжения. Система управления (Рис. 66) включает в себя микропроцессорную систему, реализующую управление по правилам нечеткой логики, и преобразователь частоты, позволяющий регулировать подачу насоса изменением его частоты вращения. Функции принадлежности входных и выходных сигналов, правила принятия решений формируются на основе знаний эксперта (опытного специалиста) о ходе технологического процесса.

Значение давления Р определяется датчиком давления, сигнал с которого после двенадцатиразрядного АЦП поступает в микропроцессорную систему управления в виде целого числа (от 0 до 4000). Положим, что значение требуемого давления находится на середине диапазона измерения датчика.

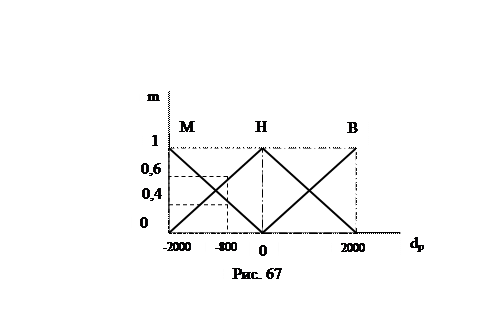
Заданное давление Р_зад примем равным 2000. Тогда отклонение текущего давления (ошибка регулирования) d_p от заданного значения находится в диапазоне от минус 2000 до плюс 2000. Для перехода к нечетким переменным по отклонению давления примем стандартную форму функций

принадлежности трех термов: уменьшить (М), норма (Н) и увеличить (В) (рис. 67).

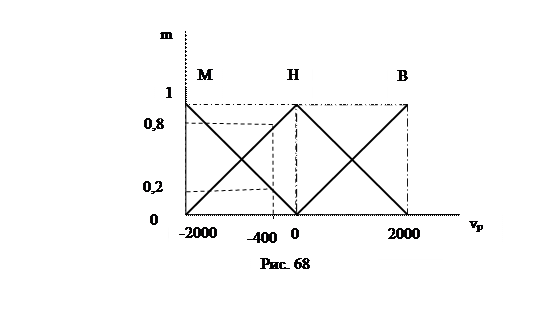
Чтобы более качественно управлять процессом, вычисляется также скорость изменения давления v_p, которая может принимать значения от -2000 до +2000. Для перехода к нечетким переменным скорости изменения давления примем стандартную форму функций принадлежности трех термов: уменьшить (М), норма(Н) и увеличить (В), (рис. 68).

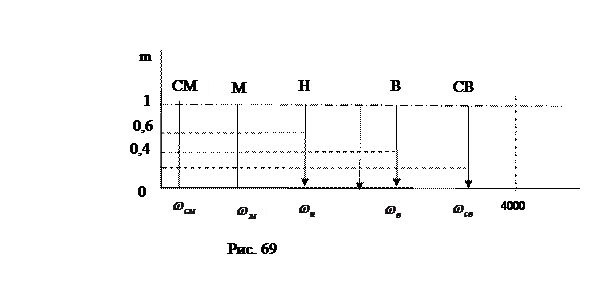
Для регулирования с помощью преобразователя частоты скорости электропривода насоса используем сигнал задания скорости u_w, который поступает с выхода ЦАП для микропроцессорной системы управления. Формированием управляющего сигнала обеспечивается изменение частоты вращения 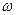, которое определяется целым числом в диапазоне от 0 до 4000. В лингвистических переменных нечеткой логики управление изменением частоты вращения может быть представлено пятью термами: сильно уменьшить (СМ), уменьшить (М), норма (Н), увеличить (В) и сильно увеличить (СВ), (рис. 69).

Если давление меньше и его значение не изменяется, то частоту вращения насоса увеличиваем. Через нечеткие переменные это правило запишем следующим образом: если d_p = M и v_p = Н, то 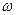= В.

Если давление меньше и его значение уменьшается, то частоту вращения насоса сильно увеличиваем. Через нечеткие переменные это правило можно записать так: если d_p = M и v_p = M, то 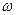= СВ.

Аналогично составляются остальные правила. Если анализировать все возможные состояния условий, то для рассматриваемого случая можно составить девять правил. Совокупность всех правил удобно представить в виде таблицы, в которой столбцы соответствуют условиям одного параметра, строки – условиям другого параметра, а на их пересечениях записываются выводы, соответствующие этим условиям (табл. 3).

Таблица 3.

Отклонение давления dp	Скорость изменения давления vp
М	Н	В
М	СВ	В	Н
Н	В	Н	М
В	Н	М	СМ

В качестве метода дефазификации примем метод центра тяжести. Рассмотрим, как определяется управление в некоторой точке движения системы.

Допустим, имеет место отклонение давления, равное -800, оно продолжает снижаться со скоростью -400. В этом случае термы М и Н отклонения давления имеют степень принадлежности 0,4 и 0,6 соответственно (см. рис. 59), а термы М и Н скорости изменения давления равны 0,2 и 0,8 (см. рис. 60). Остальные термы имеют степень принадлежности, равную 0. Для принятой формы записи правил степень принадлежности антецедента каждого правила определяется по минимуму всех условий, т.е. для вывода имеют значения правила, содержащие условия с ненулевыми степенями принадлежности:

1. Если d_p = М и v_p = М, то 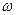=СВ;
2. » d_p = М и v_p = Н, » 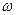=В;
3. » d_p = Н и v_p = М, » 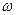=В;
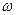4. » d_p = Н и v_p = Н, » =Н.

Каждое из этих правил дает степень принадлежности выводу по минимуму:

1. m_СВ( 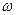) = min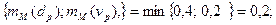

2. m_В( 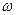) = min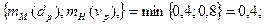

3. m_В( 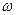) = min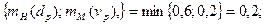

4. m_Н( 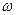) = min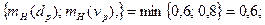

На втором шаге формирования нечеткого вывода определим степень принадлежности термов выходной переменной по максимуму. Например, выражения п.п. 2 и 3 дают разные значения степени принадлежности для терма В, но берется максимальное:

m_В( 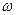) = max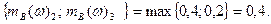

Таким образом, при данном состоянии входных сигналов степени принадлежности термов выходной переменной имеют значения (см. рис. 61):

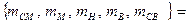
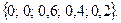
Для перехода от нечетких выводов к управляющему воздействию используем формулу дефазификации по методу центра тяжести:

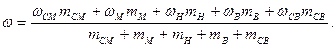
Подставив в формулу численные значения, получим

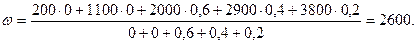
Таким образом, получено значение сигнала управления приводом насоса.

Затем эти операции повторяются с большой частотой, т. е. работа нечеткого логического регулятора носит дискретный по времени характер, и его можно рассматривать как импульсный цифровой регулятор.

Пример 11.