Унитар матрицалардың анықтамасы және қасиеттері
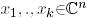 векторлар жүйесі ортогональ деп аталады, егер
векторлар жүйесі ортогональ деп аталады, егер
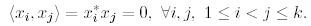
Егер де бұл векторлар нормаланған болса, яғни
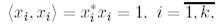
онда мұндай жүйені ортонормаланған деп атайды.
Теорема 1. Кез келген ортонормаланған жүйе сызықты тәуелсіз болып табылады.
Дәлелдеуі.  ортонормаланған векторлар жүйесі үшін
ортонормаланған векторлар жүйесі үшін
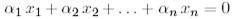
теңдігін қарастырайық және ол  болған кезде ғана орындалатындығын көрсетейік. Теңдікті оң жағынан
болған кезде ғана орындалатындығын көрсетейік. Теңдікті оң жағынан
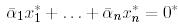
түйіндесіне көбейтіп, мынаны аламыз:
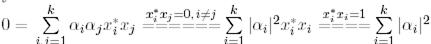
ал бұл 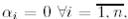 болғанда ғана мүмкін, бұдан
болғанда ғана мүмкін, бұдан  жүйесінің сызықтық тәуелсіздігі шығады.
жүйесінің сызықтық тәуелсіздігі шығады.
Кез келген сызықтық тәуелсіз векторлар жүйесін берілген жүйенің сызықтық қабықшасындай болатын ортонормаланған жүйеге түрлендіруге болады. Мұндай түрлендіруді Грам-Шмидтің ортогоналдау процессін қолданып жүргізуге болады.
Айталық  - комплексті векторлық кеңістіктегі
- комплексті векторлық кеңістіктегі 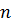 сызықтық тәуелсіз векторлар жүйесі және
сызықтық тәуелсіз векторлар жүйесі және  - ізделінді ортонормаланған жүйе болсын.
- ізделінді ортонормаланған жүйе болсын. 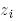 векторлары төмендегі формулалар бойынша рекуррентті есептеледі:
векторлары төмендегі формулалар бойынша рекуррентті есептеледі:
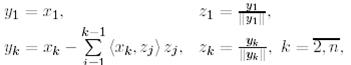 (1)
(1)
мұндағы 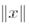 -
- 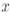 векторының евклид ұзындығы.
векторының евклид ұзындығы.
Мысал 1. (Грам-Шмидтің ортогоналдау процессі).
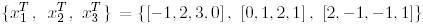
Сызықтық тәуелсіз векторлар жүйесін ортонормалайық.
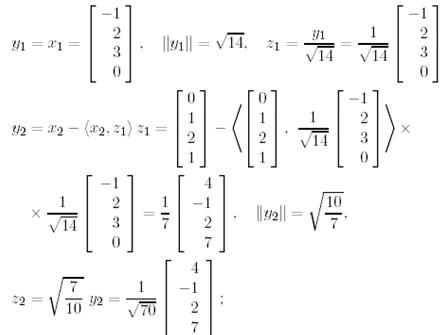
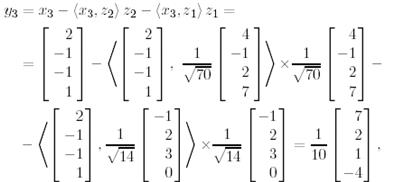
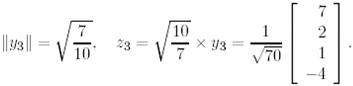
Грам-Шмидт процессінің әрбір 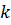 -шы қадамында
-шы қадамында  векторлары тек қана алғашқы
векторлары тек қана алғашқы 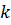 сызықтық тәуелсіз векторлардың
сызықтық тәуелсіз векторлардың  сызықтық комбинациясы түрінде өрнектеледі, яғни
сызықтық комбинациясы түрінде өрнектеледі, яғни
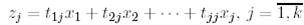 (2)
(2)
болатындай 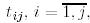 сандары бар болады.
сандары бар болады.
Грам-Шмидт процессін кез келген ақырлы немесе саналымды (сызықтық тәуелсіз болуы міндетті емес) векторлар жүйесіне қолдануға болады.
Анықтама 1. 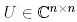 матрицасы унитар деп аталады, егер
матрицасы унитар деп аталады, егер 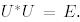 болса. Егер сонымен қатар
болса. Егер сонымен қатар 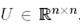 болса, онда
болса, онда 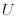 ортогональды деп аталады.
ортогональды деп аталады.
Мысал 2. (Унитар матрица). Айталық 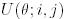 мына түрге ие болсын:
мына түрге ие болсын:

мұнда 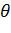 – нақты параметр. Бұл матрица бірлік матрицадан
– нақты параметр. Бұл матрица бірлік матрицадан 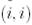 және
және 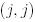 позицияларындағы элементтерімен ғана ерекшеленеді, мұнда олар сәйкесінше
позицияларындағы элементтерімен ғана ерекшеленеді, мұнда олар сәйкесінше 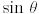 және
және 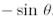 алмастырылады.
алмастырылады. 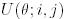 матрицасы
матрицасы  -ға тисті кез келген
-ға тисті кез келген 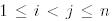 индекстер жұбы және кез келген
индекстер жұбы және кез келген 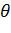 бұрышының шамасы үшін унитар (ортогональді) болып табылады. Мысалы,
бұрышының шамасы үшін унитар (ортогональді) болып табылады. Мысалы, 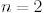 болғанда мынаны аламыз:
болғанда мынаны аламыз:
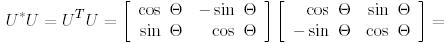
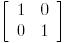 .
.
Теорема 2. (унитарлылық критерийі жайлы). Төмедегі тұжырымдар 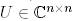 матрицасы үшін эквивалентті болады:
матрицасы үшін эквивалентті болады:
1. 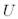 унитарлы;
унитарлы;
2. 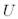 ерекше емес және
ерекше емес және 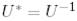 ;
;
3. 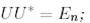
4. 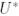 унитарлы;
унитарлы;
5. 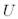 -ң бағандары ортонормаланған жүйе құрайды;
-ң бағандары ортонормаланған жүйе құрайды;
6.  -ң жолдары ортонормаланған жүйе құрайды;
-ң жолдары ортонормаланған жүйе құрайды;
7. Кез келген 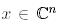 векторы үшін
векторы үшін 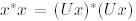 теңдігі орындалады (яғни унитарлы матрицалар изометриялы).
теңдігі орындалады (яғни унитарлы матрицалар изометриялы).
Теорема 3(QR-жіктелу жайлы). Егер 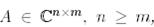 болса, онда ортонормаланған бағандары бар
болса, онда ортонормаланған бағандары бар 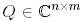 матрицасы және
матрицасы және
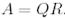
болатындай 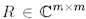 жоғары үшбұрышты матрица бар болады. Егер
жоғары үшбұрышты матрица бар болады. Егер 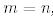 болса, онда Q унитарлы.
болса, онда Q унитарлы.
Дәлелдеуі. Егер 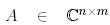 және
және 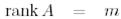 болса, онда А матрицасының QR-жіктелуі А матрицасының бағандарына Грам-Шмидтің процессін қолданғанда
болса, онда А матрицасының QR-жіктелуі А матрицасының бағандарына Грам-Шмидтің процессін қолданғанда 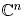 -де сызықтық тәуелсіз жүйені құрайтын нәтиженің матрицалық жазылуын аламыз.
-де сызықтық тәуелсіз жүйені құрайтын нәтиженің матрицалық жазылуын аламыз.
Айталық, 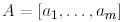 матрицаның бағандары сызықтық тәуелсіз болсын. Грам-Шмидтің алгоритмін осы жағдай үшін жалпылайық. Грам-Шмидтің ортогоналдау процессінің нәтижесінде
матрицаның бағандары сызықтық тәуелсіз болсын. Грам-Шмидтің алгоритмін осы жағдай үшін жалпылайық. Грам-Шмидтің ортогоналдау процессінің нәтижесінде  болатындай
болатындай 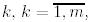 -лар үшін (яғни
-лар үшін (яғни 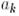 бұл
бұл 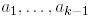 сызықтық комбинация болып табылады),
сызықтық комбинация болып табылады), 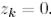 болсын делік. Керісінше жағдайда,
болсын делік. Керісінше жағдайда, 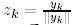 (қарапайым Грам-Шмидт процессіндегідей).
(қарапайым Грам-Шмидт процессіндегідей).
 векторлары ортогональ жүйені құрайды, оның әрбір элементі нормаланған немес нөлдік.
векторлары ортогональ жүйені құрайды, оның әрбір элементі нормаланған немес нөлдік.
Әрбір 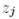 векторы – бұл
векторы – бұл  векторларының сызықтық комбинациясы және керісінше. Бұдан,
векторларының сызықтық комбинациясы және керісінше. Бұдан,
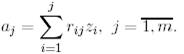 (3)
(3)
болатындай 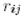 сандары табылады.
сандары табылады.
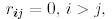
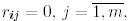 , егер
, егер 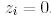 болса. (4)
болса. (4)
Осылайша,  -нан жоғарыда сипатталған процедураның көмегімен жоғары үшбұрышты матрицаны
-нан жоғарыда сипатталған процедураның көмегімен жоғары үшбұрышты матрицаны
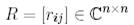
және  векторларын табайық.
векторларын табайық.
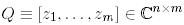
Матрицасы ортогонал бағандардан тұрады (кейбіреулері нөлдік болуы мүмкін) және (3)-ң негізінде 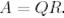 болады.
болады.
Егер 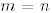 және
және 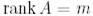 (яғни А ерекше емес) болса, онда Q – 2-теореманың (5-қасиеті бойынша) унитарлы және
(яғни А ерекше емес) болса, онда Q – 2-теореманың (5-қасиеті бойынша) унитарлы және 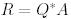 матрицасының барлық диагональды элементтері нөлден өзгеше. Бұл жағдайда
матрицасының барлық диагональды элементтері нөлден өзгеше. Бұл жағдайда 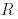 матрицасы – жоғары үшбұрышты болғандықтан,
матрицасы – жоғары үшбұрышты болғандықтан, 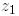 векторы
векторы 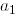 векторының еселігі болады және
векторының еселігі болады және 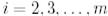 болғанда
болғанда 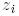 векторы бірөлшемді кеңістікте жатады, ол
векторы бірөлшемді кеңістікте жатады, ол  векторларының сызықтық қабықшасындағы
векторларының сызықтық қабықшасындағы 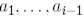 векторларының сызықтық қабықшасының ортогональ толықтауышы болып табылады. Бұдан, әрбір
векторларының сызықтық қабықшасының ортогональ толықтауышы болып табылады. Бұдан, әрбір 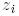 векторы модулі бойынша 1-ге тең скаляр көбейткішке дейінгі дәлдікпен бірмәнді анықталады. Сондықтан да
векторы модулі бойынша 1-ге тең скаляр көбейткішке дейінгі дәлдікпен бірмәнді анықталады. Сондықтан да 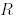 -ды
-ды 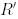 -қа ауыстырып:
-қа ауыстырып:
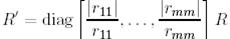
және 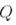 -ды
-ды 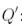 -қа ауыстырып:
-қа ауыстырып:
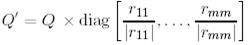
теореманың тұжырымында айтылған сол жалғыз жіктеуді аламыз.
Егер А матрицасының бағандары тәуелді болса, онда Q-дан нөлдік емес бағандар жиынын (ортонормаланған) алып және оны 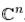 -гі ортонормаланған базиске дейін толықтырамыз. Мұндай әдіспен алынған жаңа векторларды
-гі ортонормаланған базиске дейін толықтырамыз. Мұндай әдіспен алынған жаңа векторларды  деп белгілейміз. Енді Q-дағы бірінші нөолдік бағанды
деп белгілейміз. Енді Q-дағы бірінші нөолдік бағанды 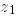 менғ ал екіншіні
менғ ал екіншіні 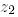 -мен және т.с.с. ауыстырамыз. Алынған матрицаны
-мен және т.с.с. ауыстырамыз. Алынған матрицаны 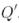 деп белгілейік. Ол ортонормаланған бағандардан тұрады және
деп белгілейік. Ол ортонормаланған бағандардан тұрады және  , себебі
, себебі 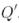 -ғы жаңа бағандар
-ғы жаңа бағандар 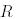 -ғы нөлдік жолдарға сәйкес келеді. Осылайша,
-ғы нөлдік жолдарға сәйкес келеді. Осылайша, 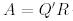 - қажетті түрдегі жіктеу.
- қажетті түрдегі жіктеу.
Мысал 3. (QR-жіктеу).
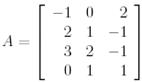
матрицасы үшін QR-жіктеуін құрайық. Ол үшін Грам-Шмидтің ортогоналдау процессін қолданайық. А матрицасының бағандарын
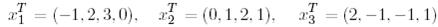
деп белгілейік. 1-мысалда көрсетілгендей Грам-Шмидтің ортогоналдау процессінің нәтижесінде 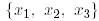 векторлар жүйесі
векторлар жүйесі 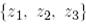 ортонормаланған векторлар жүйесіне түрленеді, мұнда
ортонормаланған векторлар жүйесіне түрленеді, мұнда
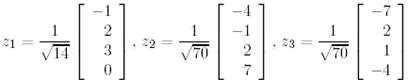
сонымен қатар,
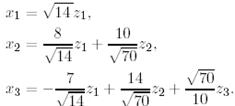
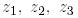 векторларынан матрица құрамыз
векторларынан матрица құрамыз
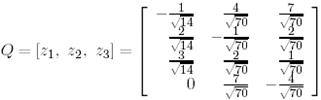
Онда 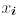 және
және 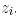
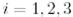 байланыстыратын теңдіктерден мынаны аламыз:
байланыстыратын теңдіктерден мынаны аламыз:
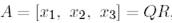 , мұндағы
, мұндағы 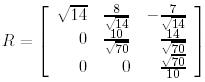 .
.
2. Унитар ұқсастық
Унитар матрица үшін 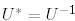 болса, онда
болса, онда 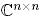 анықталған
анықталған 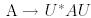 түрлендіруі ұқсас болып табылады, ол унитар ұқсастық деп аталады.
түрлендіруі ұқсас болып табылады, ол унитар ұқсастық деп аталады.
Анықтама 2. 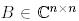 матрицасы
матрицасы 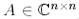 матрицасына унитар ұқсас деп аталады, егер
матрицасына унитар ұқсас деп аталады, егер 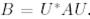 болатындай
болатындай 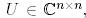 унитар матрицасы бар болса. Егер
унитар матрицасы бар болса. Егер 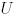 - ды нақты етіп таңдап алуға болса(ендеше ортогоналды болатындай), онда
- ды нақты етіп таңдап алуға болса(ендеше ортогоналды болатындай), онда 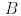 матрицасы А матрицасына ортогональ ұқсас деп аталады.
матрицасы А матрицасына ортогональ ұқсас деп аталады.
Унитар матрицалардың екі арнайы түрін қарастырайық, олар унитар ұқсастық түрлендіруін жүзеге асырады, бұл меншікті мәндерді есептеу үшін маңызды.
Мысал 4. (Жалпақ (тегіс) айналу). 2-мысалдағы 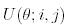 матрицасы жазықтықта
матрицасы жазықтықта 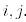 координатының (
координатының ( 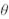 бұрышқа) айналуын жүзеге асырады. Егер матрица сол жағынан
бұрышқа) айналуын жүзеге асырады. Егер матрица сол жағынан 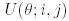 -ға көбейтілсе, ендеше мұнда тек қана
-ға көбейтілсе, ендеше мұнда тек қана 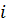 -ші және
-ші және 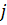 -ші жол өзгереді, ал егер матрица оң жағынан көбейтілсе, онда тек қана
-ші жол өзгереді, ал егер матрица оң жағынан көбейтілсе, онда тек қана 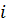 -ші және
-ші және 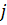 -ші баған өзгереді. Осылайша,
-ші баған өзгереді. Осылайша, 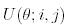 көмегімен жүзеге асырылатын унитар ұқсас матрицаға көшкенде тек қана
көмегімен жүзеге асырылатын унитар ұқсас матрицаға көшкенде тек қана 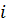 және
және 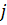 нөмірлі жол және бағандар өзгереді. Тегіс айналу көмегімен алынатын унитар ұқсастық меншікті мәндерді есептеген кезде қолданылады.
нөмірлі жол және бағандар өзгереді. Тегіс айналу көмегімен алынатын унитар ұқсастық меншікті мәндерді есептеген кезде қолданылады.
Мысал 5. (Хаусхолдер түрлендіруі). Кез келген нөлдік емес 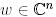 векторын алайық және матрица құрайық
векторын алайық және матрица құрайық
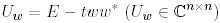
мұндағы 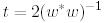 .
. 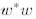 -бұл оң скаляр,
-бұл оң скаляр, 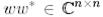 - матрица екендігін ескерейік. Егер
- матрица екендігін ескерейік. Егер 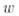 векторы нормаланған
векторы нормаланған 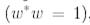 болса, онда
болса, онда 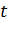 2-ге тең болуы керек, ал
2-ге тең болуы керек, ал 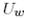 матрицасы мына түрге ие болу керек:
матрицасы мына түрге ие болу керек:
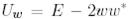 .
.
Әдетте 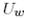 матрицасын алдын ала
матрицасын алдын ала 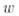 нормаланған векторын таңдап алу арқылы құрады.
нормаланған векторын таңдап алу арқылы құрады.
Кез келген 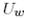 матрицасы Хаусхолдер түрлендіруі деп аталады.
матрицасы Хаусхолдер түрлендіруі деп аталады.
Теорема 4. 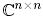 -ға тиісті А және В унитарлы ұқсас матрицалары үшін келесі теңдік орындалады:
-ға тиісті А және В унитарлы ұқсас матрицалары үшін келесі теңдік орындалады:
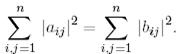
Дәлелдеуі ұқсас үрлендіруге қатысты матрица ізінің инварианттылығының негізінде алынатын төмендегі теңдіктер тізбегінен алынады:
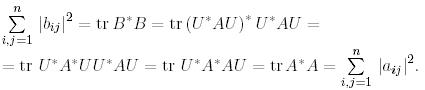
Теорема 5. (Унитар триангулярлау жайлы Шур теоремасы). Айталық 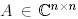 матрицасы берілсін және оның қандай да бір
матрицасы берілсін және оның қандай да бір  меншікті мәндерінің реті бекітілсін. Онда
меншікті мәндерінің реті бекітілсін. Онда
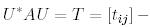
диагоналында 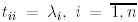 элементі тұратын жоғары үшбұрышты матрица болатындай
элементі тұратын жоғары үшбұрышты матрица болатындай 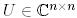 унитар матрицасы бар болады. сонымен қатар, егер
унитар матрицасы бар болады. сонымен қатар, егер 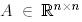 және оның барлық меншікті мәндері нақты болса, онда
және оның барлық меншікті мәндері нақты болса, онда 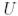 -ды ортогонал етіп таңдап алуға болады.
-ды ортогонал етіп таңдап алуға болады.
басқаша айтқанда, кез келген комплексті матрица ұқсас үшбұрышты матрицаға унитарлы болады.
Мысалы, төмендегі 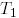 және
және 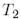 матрицалары
матрицалары 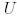 түрлендіруінің унитар матрицасымен унитар ұқсас:
түрлендіруінің унитар матрицасымен унитар ұқсас:
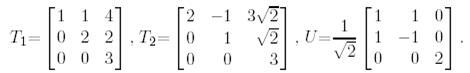
Салдар 1. Айталық 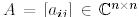 болсын.
болсын. 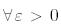 үшін
үшін 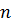 әр түрл меншікті мәні бар (ендеше, диагоналданатын) және
әр түрл меншікті мәні бар (ендеше, диагоналданатын) және
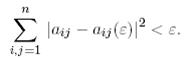
болатындай 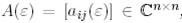 матрицасы бар болады.
матрицасы бар болады.
Басқаша айтқанда, кез келген матрица үшін оған соншалықты жақын диагональданатын матрица бар болады.
Салдар 2. Айталық 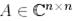 болсын.
болсын. 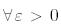 үшін
үшін
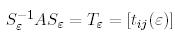
жоғары үшбұрышты матрица және 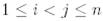 үшін
үшін 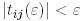 болатындай, ерекше емес
болатындай, ерекше емес 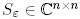 матрицасы бар болады.
матрицасы бар болады.
Басқаша айтқанда, кез келген матрица кез келген кішкентай диагональдан тыс элементтері бар жоғары үшбұрышты матрицаға ұқсас болады.
Теорема 6. Егер 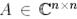 матрицасы
матрицасы  меншікті мәндеріне (еселігін ескергенде) ие болса, онда
меншікті мәндеріне (еселігін ескергенде) ие болса, онда
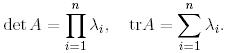
Дәлелдеуі. Шур теоремасын қолданып 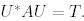 деп жазамыз. Онда іздің және матрицаның анықтауышының ұқсас түрлендіруге қатысты инварианттылығын ескерсек мынаны аламыз:
деп жазамыз. Онда іздің және матрицаның анықтауышының ұқсас түрлендіруге қатысты инварианттылығын ескерсек мынаны аламыз:
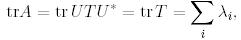 (5)
(5)
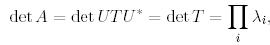 (6)
(6)
ал бұл дәлелдеуді аяқтайды.
