Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси

Для вывода уравнения динамики вращательного движения твердого тела используем теорему о кинетической энергии: работа результирующей всех сил, действующих на тело, идет на приращение кинетической энергии: dA=dE_k.

Пусть к телу, закрепленному на оси О, в горизонтальной плоскости приложена внешняя сила F (рис.5).

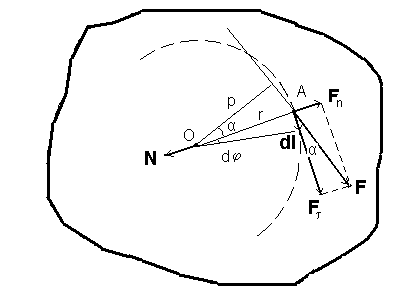Рис.5.

Напомним, что элементарной работой dA силы F называется скалярное произведение силы F на бесконечно малое перемещение dl:

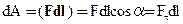
где a - угол между направлением силы и направлением перемещения.

Отметим, что нормальная составляющая силы F_n (в отличие от тангенциальной F_τ) и сила реакции опоры N работы не совершают, так как они перпендикулярны направлению перемещения.

Элемент dl=rdj при небольших углах поворота dj (r – радиус-вектор элемента тела). Тогда работа этой силы записывается следующим образом:

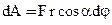. (19)

Выражение Fr cosa является моментом силы (произведение силы F на плечо p=r cosa):

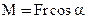(20)

Тогда работа равна

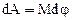. (21)

Эта работа затрачивается на изменение кинетической энергии вращения:

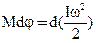. (22)

Если I=const, то после дифференцирования правой части получим:

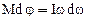
или, так как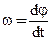

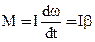, (23)

где 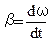- угловое ускорение.

Выражение (23) является уравнением динамики вращательного движения твердого тела относительно неподвижной оси,которое лучше с точки зрения причинно-следственных связей представить как:

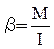. (24)