Теорема о проецировании прямого угла

Вопрос

Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны.

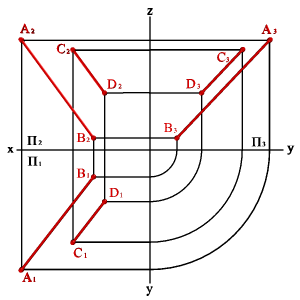
Пересекающиеся прямые.

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.

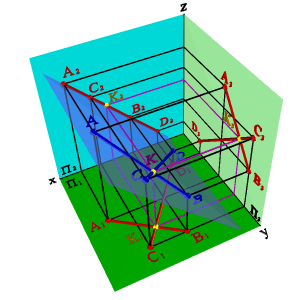
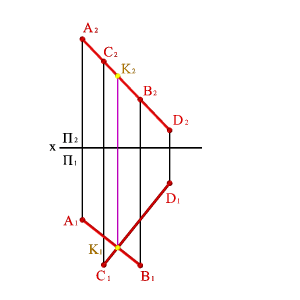Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи

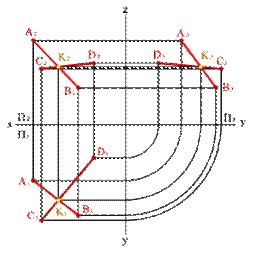
Скрещивающимися называются две прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

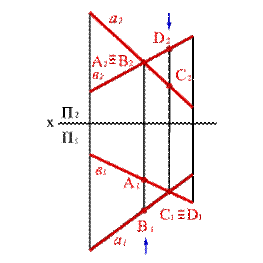
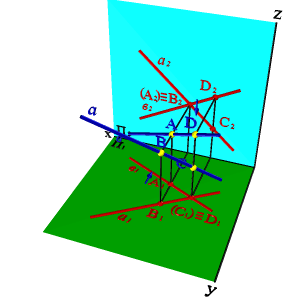
Если у точек равны две одноименные координаты, то они называются конкурирующими. Конкурирующие точки расположены на одной проецирующей прямой.

Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В лежащая на прямой в,следовательно, прямая впроходит в этом месте ближе прямой а и фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и Д решение аналогично).

Этот способ определения видимости по конкурентным точкам. В данном случае точки А и В- фронтально конкурирующие, а С и Д -горизонтально конкурирующие.

Теорема о проецировании прямого угла

Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения.

5 вопрос

Плоскость – одно из основных понятий геометрии.

1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;

2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Общее уравнение плоскости:

Ax+By+Cz+D=0,

где А, В, С, и D - постоянные, причем А, В и С одновременно не равны нулю.

Способы графического задания плоскостей

Положение плоскости в пространстве можно определить:

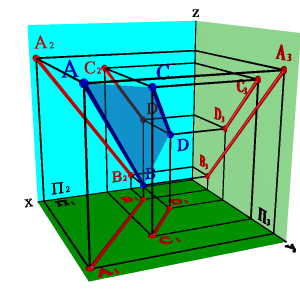
1. Тремя точками, не лежащими на одной прямой линии

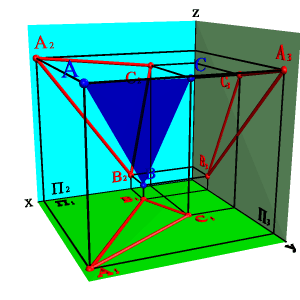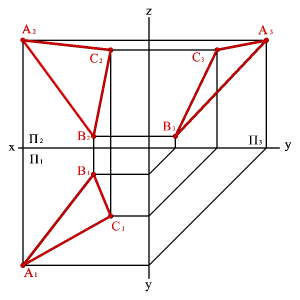2. Прямой линией и точкой, не принадлежащей этой прямой

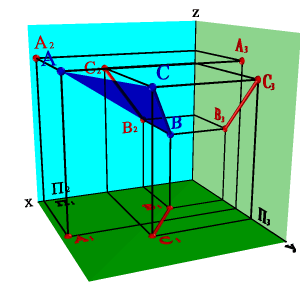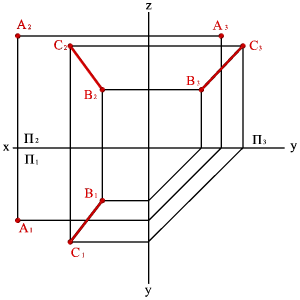3. Двумя пересекающимися прямыми

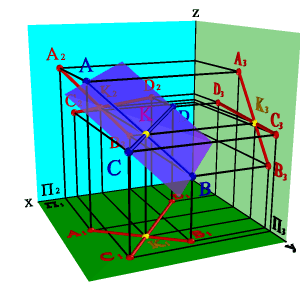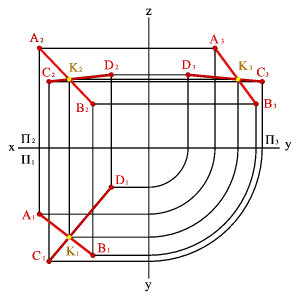4. Двумя параллельными прямыми

Различное положение плоскости относительно плоскостей проекций

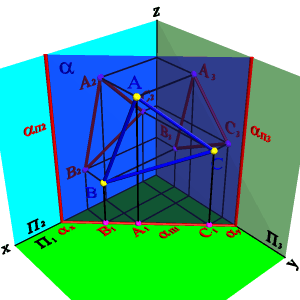
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций

2. Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими.
горизонтально проецирующей плоскостью

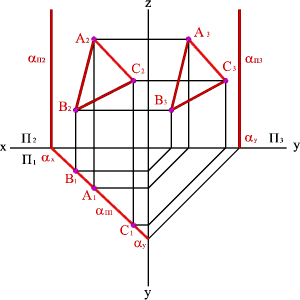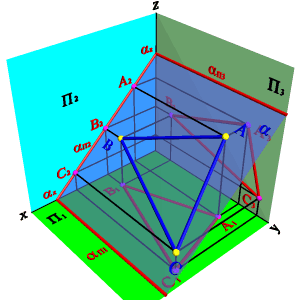
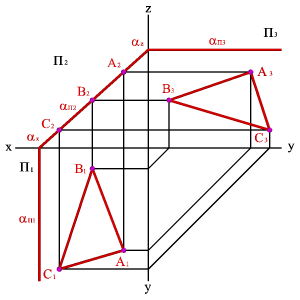
2.2. Плоскость перпендикулярная фронтальной плоскости проекций (a^П₂)- фронтально проецирующая плоскость.

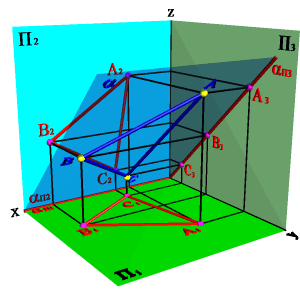
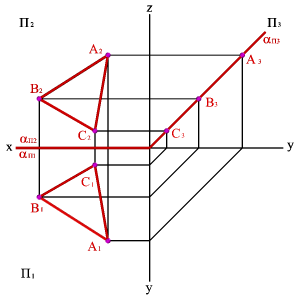
2.3. Плоскость перпендикулярная профильной плоскости ( ^aП₃) - профильно проецирующая плоскость.

3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:

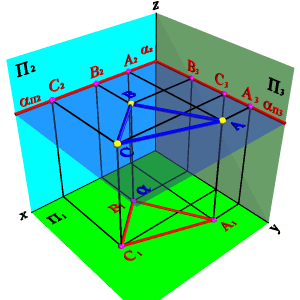
3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (aП₁) - (^aП₂,^aП₃

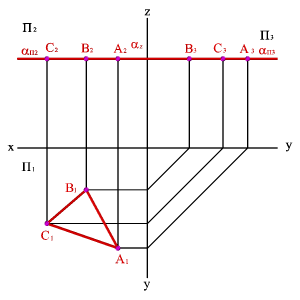3.2. Фронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (aП₂), (a^П₁, a^П₃). Любая фигура в этой плоскости проецируется на плоскость П₂ без искажения, а на плоскости П₁ и П₃ в прямые - следы плоскости a_П1 и a_П3

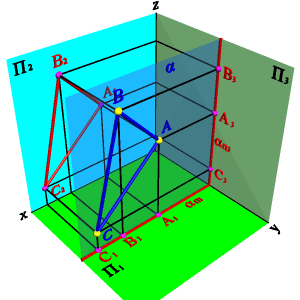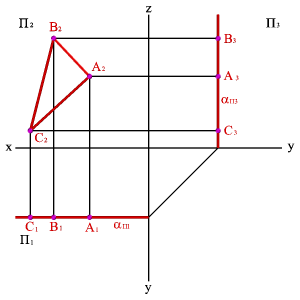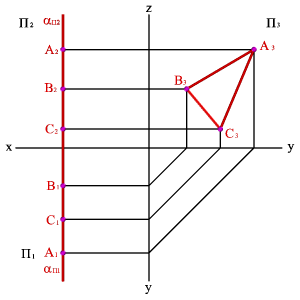
3.3.Профильная плоскость - плоскость параллельная профильной плоскости проекций (a//П₃), (a^П₁, a^П₂).Любая фигура в этой плоскости проецируется на плоскость П₃ без искажения, а на плоскости П₁ и П₂ в прямые - следы плоскости a_П1 и a_П2

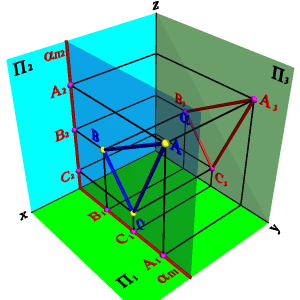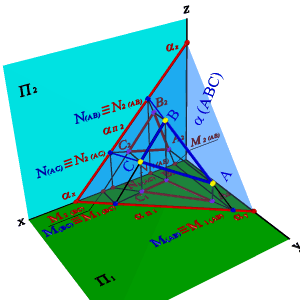
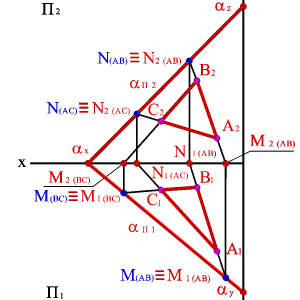
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают: горизонтальный, фронтальный и профильный следы плоскости.

6 вопрос

Взаимное расположение прямой и плоскости

Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей.

Прямая линия, принадлежащая плоскости

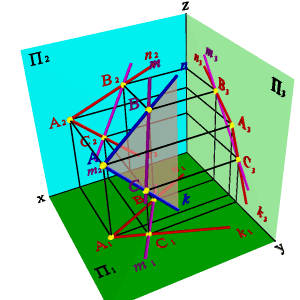
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости

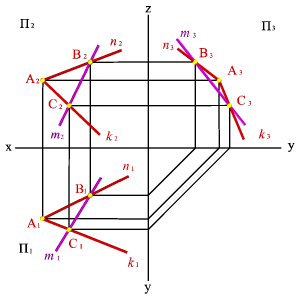Аксиома 2.Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

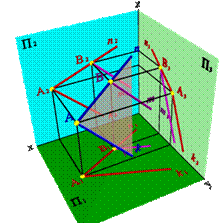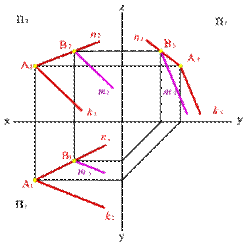Главные линии в плоскости

Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:

1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎСВА, hP₁, h₂Ох,h₃Оy)

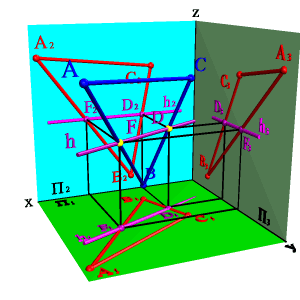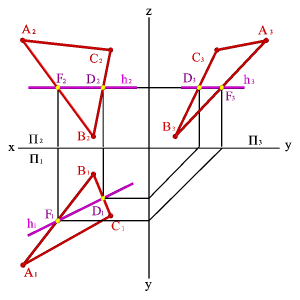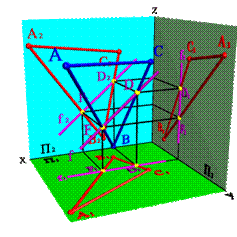
2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎСВА, fP₂, f₁Ох, f₃Оz)

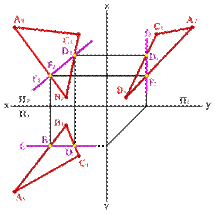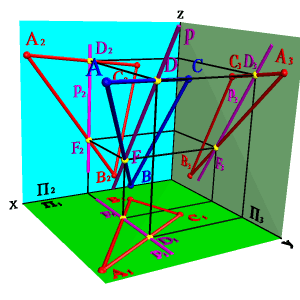
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (рÎСВА, рP₃, р₁^Ох, р₂^Ох)

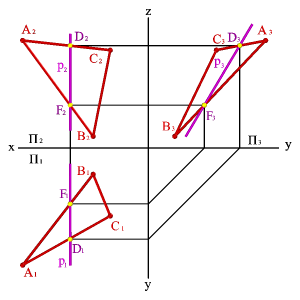Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций

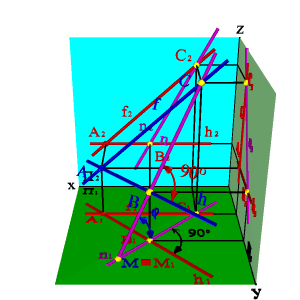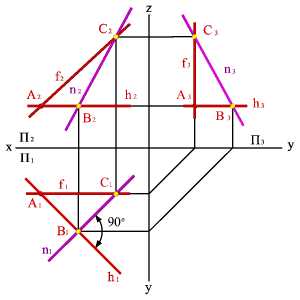7 вопрос

Возможны два случая взаимного расположения двух плоскостей в пространстве:

• Параллельны
• Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в противном случаи они пересекаются.

Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.