Түрлендіру әдісін қолдану
Біз геометрияның теориялық сұрақтарын қарастырғанымызда түрлендіру әдісінің кейбір қолдануларын қарастырдық. Мысалы, қозғалысты фигуралар теңдігін анықтағанда, ұқсас түрлендіруді үшбұрыштар ұқсастығын оқып-үйренгенде.
Түрлендірулер әдісін түрлі геометриялық есептер шығаруда қолдануды қарастырайық.
19-мысал. АОВ тікбұрыштың ішінен М нүктесі алынған.
| Сурет - 46 |
 SOA(M) = M1, SOB(M) = М2
SOA(M) = M1, SOB(M) = М2 шарттарын қанағаттандыратындай нүктелер жүргізілген. М1, О және М2 нүктелерінің бір түзудің бойында жататынын дәлелдеу керек (46- сурет)
Берілгені:  АОВ =90"
АОВ =90"
М €  АОВ
АОВ
SOA(M) = M1, SOB(M) = М2
Дәлелдеу керек: (М1, О және М2) €L
Дәлелдеу. М1, О, М2 нүктелері бір түзудің бойында жату үшін
 l=
l=  5, яғни олар вертикаль бұрыштар болуы қажет. АО ны созсақ,
5, яғни олар вертикаль бұрыштар болуы қажет. АО ны созсақ,
 АОВ= 90 °, онда
АОВ= 90 °, онда  ВОК = 90 °.
ВОК = 90 °.
Бұл арадан  5 = 90?-
5 = 90?- 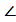 4
4
 2= 90?-
2= 90?- 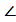 3 түрінде жазуға болады. Симметриялы нүктелердің қасиеті бойынша
3 түрінде жазуға болады. Симметриялы нүктелердің қасиеті бойынша
 4 =
4 =  3
3
 2 =
2 =  1
1
Сонымен,  5 = 90?-
5 = 90?- 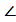 4
4
 1 = 90?-
1 = 90?-  4 яғни
4 яғни  5 =
5 =  1 вертикаль бұрыштар болады.
1 вертикаль бұрыштар болады.
Ендеше М1,О, М2 нүктелері бір түзудің бойында жатады.
 20-мысал. Берілгені: ∆АВС (47-сурет)
20-мысал. Берілгені: ∆АВС (47-сурет)
AL - биссектриса,
КМ  AL
AL
BB1  КМ
КМ
Дәлелдейтініміз: Р∆ВВ1С1 > Р∆АВС
Дәлелдеуі. ВВ1+В1С+ВС>АВ+АС+ВС
немесе ВВ1+ В1С>АС+АВ
КМ -ге қарағанда
 нүктесін табамыз. 47-сурет
нүктесін табамыз. 47-сурет
Симметриялы нүктелердің қасиеті бойынша  l=
l=  2 (1), мұндағы
2 (1), мұндағы  2+
2+  3 =
3 =  4+
4+  5 себебі: AL
5 себебі: AL  KM.
KM.
Есептің шарты бойынша  2=
2=  3, ендеше
3, ендеше  2=
2=  5 (2).
5 (2).
Жоғарыдағы (1), (2) теңдіктерден  =
=  5 болады. Демек,
5 болады. Демек,  AB -
AB -
түзу сызық. ∆  ВС1 үшбұрыштың екі қабырғаның ұзындықтарының қосындысы үшінші қабырғасының ұзындығынан артық деген қасиет бойынша С1В1 + В1В> С1А + АВ
ВС1 үшбұрыштың екі қабырғаның ұзындықтарының қосындысы үшінші қабырғасының ұзындығынан артық деген қасиет бойынша С1В1 + В1В> С1А + АВ
Себебі С1В1 = В1С, С1А = АС сонымен, В1С1+ В1В > AC + АВ теңсіздіктің екі жағына ВС-ні қоссақ, нәтижесінде В1В + В1С1 + BC>AC + АВ + ВС болады.
| Сурет 48 |
 21-мысал. Теңбүйірлі үшбұрыштың табанындағы кез келген бірнүктеден бүйір қабырғаларына дейінгі ара қашықтықтардың қосындысы үшбұрыштың бір төбесінен оған қарсы жатқан бүйір қабырғасына түсірілген биіктіктің ұзындығына тең болатынын дәлелдеу керек.
21-мысал. Теңбүйірлі үшбұрыштың табанындағы кез келген бірнүктеден бүйір қабырғаларына дейінгі ара қашықтықтардың қосындысы үшбұрыштың бір төбесінен оған қарсы жатқан бүйір қабырғасына түсірілген биіктіктің ұзындығына тең болатынын дәлелдеу керек. Берілгені: ∆АВС: АВ = ВС
М  АС, АК
АС, АК  ВС
ВС
MN  ВС
ВС
РM  AB
AB
Дәлелдеу керек: PM + МК = АК
Дәлелдеу үшін АС қабырғасына қарағанда ∆АВС-ға симметриялы үшбұрыш сызамыз, сонда АВСВ1 ромбы шығады. Р нүктесіне симметриялы Р1= S (Р) нүктені табамыз. Р мен М нүктелерін қосып, Р, М, Nнүктелерінің бір түзу бойында жататынын дәлелдейміз. Егер Р1= SАС (Р) болса, онда Р1М  АВ1
АВ1
| Сурет 49 |
 22 - мысал.Табанының ұзындығы a - ға тең, үшбұрыштың бүйір қабырғаларын О төбесінен бастап есептегенде қатынасы m болатындай бөліктерге бөлетін кесіндінің ұзындығын табу керек (49-сурет).
22 - мысал.Табанының ұзындығы a - ға тең, үшбұрыштың бүйір қабырғаларын О төбесінен бастап есептегенде қатынасы m болатындай бөліктерге бөлетін кесіндінің ұзындығын табу керек (49-сурет). Берілгені: ∆ОВС, ВС = а,
ОЕ : EC = OD : BD = m
Табатынымыз DE - ?
Шешуі: Н0к -гомотетияны қарастыралық. Егер Н0к (О) = О, Н0к (D) = В, Н0к(Е) = С, болса,
Онда ОС = к∙ОЕ, OB = к∙OD және
ВС = к ∙ DE → а = к ∙ DE —> DE= 

23-мысал. Трапецияның табандарына параллель және диагональдарының қиылысу нүктесінен өтетін, бүйір қабырғаларын қосатын кесіндісінің үзындығын табу керек.
| 50-сурет |
 Берілгені ABCD - трапеция АВ = a, DC = b (50-сурет)
Берілгені ABCD - трапеция АВ = a, DC = b (50-сурет) Табатынымыз: ЕҒ-?
Шешуі: Центрі О-нүктесі, к - коэффициенті болатын гомотетияны қарастыралық. Мұндағы О— трапецияның диагоналдарының қиылысу нүктесі.
Гомотетияның анықтамасы бойынша

 24-мысал. Үшбұрыш қабырғаларының ортасын қосқаннан (центрі - медианаларының қиылысу нүктесі) коэффициенті к = - ? болатын, әуелгі үшбұрышқа гомотетиялы үшбұрыш шығатынын дәлелдеу керек
24-мысал. Үшбұрыш қабырғаларының ортасын қосқаннан (центрі - медианаларының қиылысу нүктесі) коэффициенті к = - ? болатын, әуелгі үшбұрышқа гомотетиялы үшбұрыш шығатынын дәлелдеу керек
(51-сурет).
Берілгені: ∆АВС
| Сурет 51 |
Дәлелдейтініміз: ∆АВС және ∆А0В0С0
гомотетиялы болатынын, яғни Н  (∆АВС)=∆А0В0С0
(∆АВС)=∆А0В0С0
Шешуі: Берілген ABC үшбұрышының медианаларының табандарын төбелеріне сәйкес А0В0 және С0 деп белгілеп, оларды қоссақ, ∆А0В0С0, шығады. О - центрлі коэффициенттері К болатын және Н0к(0) = 0, Н0к (A) = А0, Н0к (B) = В0, Н0к (С) = С0 шарттарын қанағаттандыратын
| Сурет 52 |
 гомотетияны қарастырайық. Үшбұрыш медианасының белгілі қасиеті бойынша ОА0 : ОА = ОВ0 : ОВ = ОС0 : ОС =
гомотетияны қарастырайық. Үшбұрыш медианасының белгілі қасиеті бойынша ОА0 : ОА = ОВ0 : ОВ = ОС0 : ОС = -  . Сонымен, к = -
. Сонымен, к = -  бола отырып, ∆АВС мен ∆А0В0С0 гомотетиялы болады.
бола отырып, ∆АВС мен ∆А0В0С0 гомотетиялы болады.
25-мысал. ABCD - параллелограмының А төбесінен BD диагоналын және CD қабырғасын сәйкесінше P, Q нүктелерінде қиып өтетін түзу жүргізілген.
Егер  =
=  болса, онда
болса, онда  =
=  +1
+1
теңдігі орындалатынын көрсету керек.
Шешуі. Берілгендері бойынша Hкр(Р) = Р,Hкр(A) = Q, HkP(B) = D
HRp (B) = D шарттарын қанағаттандыратындай түрлендірулер жүргіземіз. Сонда 
гомотетия коэффициенті.
AB:DC =  немесе
немесе  =
= 

