Практичне заняття 17. довірчі інтервали

1. Довірчий інтервал для оцінки математичного сподівання нормального розподілу при відомому .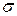

2. Довірчий інтервал для оцінки математичного сподівання нормального розподілу при невідомому .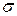

Приклад. Вимірявши 40 випадково відібраних після виготовлення деталей, знайшли вибіркову середню, що дорівнює 15 см. Із надійністю побудувати довірчий інтервал для середньої величини всієї партії деталей, якщо генеральна дисперсія дорівнює .

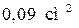Розв’язання. Для побудови довірчого інтервалу необхідно знати: 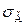, n, x.

З умови задачі маємо: 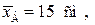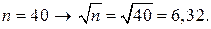Величина х обчислюється з рівняння

Знайдемо числові значення кінців довірчого інтервалу:

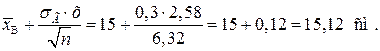
Таким чином, маємо:

.

Приклад. Маємо такі дані про розміри основних фондів (у млн грн.) на 30-ти випадково вибраних підприємствах:

4,2; 2,4; 4,9; 6,7; 4,5; 2,7; 3,9; 2,1; 5,8; 4,0;

2,8; 7,8; 4,4; 6,6; 2,0; 6,2; 7,0; 8,1; 0,7; 6,8;

9,4; 7,6; 6,3; 8,8; 6,5; 1,4; 4,6; 2,0; 7,2; 9,1.

Побудувати інтервальний статистичний розподіл із довжиною кроку h = 2млн грн.

З надійністю знайти довірчий інтервал для , якщо 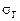= 5 млн грн.

Розв’язання. Інтервальний статистичний розподіл буде таким:

h = 2 млн грн.	2–4	4–6	6–8	8–10
ni

Для визначення 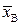необхідно побудувати дискретний статистичний розподіл, що має такий вигляд:

ni

.

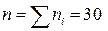Тоді

Для побудови довірчого інтервалу із заданою надійністю необхідно знайти х:

Обчислюємо кінці інтервалу:

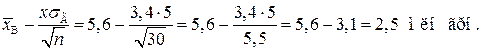
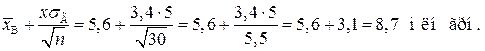
Отже, довірчий інтервал для буде .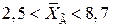

Приклад. Якого значення має набувати надійність оцінки γ, щоб за обсягу вибірки n = 100 похибка її не перевищувала 0,01 при .

Розв’язання. Позначимо похибку вибірки

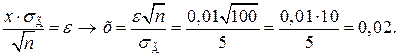
Далі маємо:

Як бачимо, надійність мала.

Приклад. Визначити обсяг вибірки n,за якого похибка гарантується з імовірністю 0,999, якщо .

Розв’язання. За умовою задачі 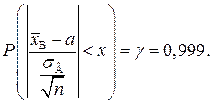Оскільки то дістанемо: Величину х знаходимо з рівності Тоді

Приклад. Випадково вибрана партія з двадцяти приладів була випробувана щодо терміну безвідмовної роботи кожного з них t_і. Результати випробувань наведено у вигляді дискретного статистичного розподілу:

ti
ni

З надійністю побудувати довірчий інтервал для «а» (середнього часу безвідмовної роботи приладу).

Розв’язання. Для побудови довірчого інтервалу необхідно знайти середнє вибіркове і виправлене середнє квадратичне відхилення.

Обчислимо :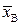

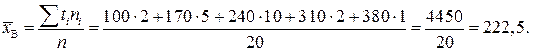
Отже, дістали

Визначимо D_B:

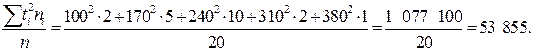
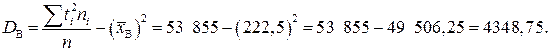
Отже, D_B = 4348,75.

Виправлене середнє квадратичне відхилення дорівнюватиме:

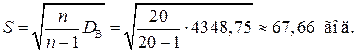
За таблицею значень 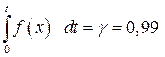(додаток 3) розподілу Ст’юдента за заданою надійністю і числом ступенів свободи = 20 – 1 = 19 знаходимо значення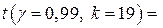

Обчислимо кінці довірчого інтервалу:

Отже, з надійністю можна стверджувати, що 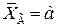буде міститися в інтервалі .

При великих обсягах вибірки, а саме: на підставі центральної граничної теореми теорії ймовірностей (теореми Ляпунова) розподіл Ст’юдента наближається до нормального закону. У цьому разі знаходиться за таблицею значень функції Лапласа.

Приклад. У таблиці наведено відхилення діаметрів валиків, оброблених на верстаті, від номінального розміру:

h= 5 мк	0–5	5–10	10–15	15–20	20–25
ni

Із надійністю побудувати довірчий інтервал для .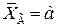

Розв’язання.Для побудови довірчого інтервалу необхідно знайти 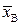, S.

Для цього від інтервального статистичного розподілу, наведеного в умові задачі, необхідно перейти до дискретного, а саме:

	2,5	7,5	12,5	17,5	22,5
ni

Обчислимо :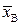

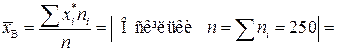
Отже,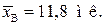

Визначимо D_B:

Обчислимо виправлене середнє квадратичне відхилення S:

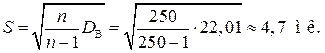
З огляду на великий (n = 250) обсяг вибірки можна вважати, що розподіл Ст’юдента близький до нормального закону. Тоді за таблицею значення функції Лапласа

Обчислимо кінці інтервалів:

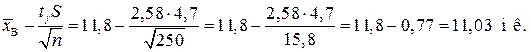
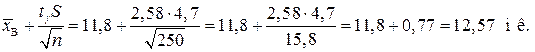
Отож, довірчий інтервал для середнього значення відхилень буде таким: .

Звідси з надійністю (99%) можна стверджувати, що а 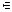[11,03 мк; 12,57 мк].