Построение годографа разомкнутой ИСАУ

Задание на расчет.

1. Преобразовать исходную структурную схему к типовому виду; определить не­прерывную передаточную функцию приведенной непрерывной части разомкнутой импульсной системы ;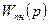

2. По 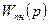найти дискретную передаточную функцию разомкнутой импульсной системы ;

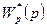3. Построить годограф разомкнутой импульсной САУ:

- По выражению ;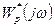

- По годографу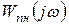

4. Оценить устойчивость замкнутой импульсной САУ и найти предельный коэффициент усиления:

- По критерию Найквиста;

- По критерию Гурвица;

- По корням характеристического уравнения

Построить переходной процесс для замкнутой импульсной САУ.

Определить статическую и кинетическую ошибки замкнутой импульсной САУ.

1. Преобразование исходной структурной схемы к типовому виду и определение не­прерывной передаточной функции приведенной непрерывной части разомкнутой импульсной системы .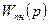

Приведем исходную структурную схему:

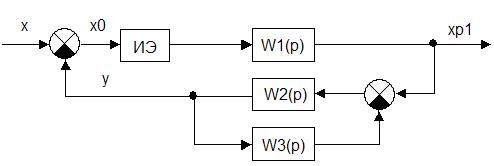
Рис.1. Исходная структурная схема.

Приведем схему замещения импульсного элемента:

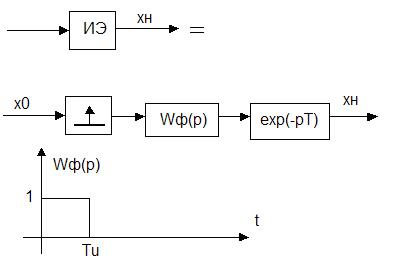
Рис.2. Схема замещения импульсного элемента.

Запишем исходные данные:

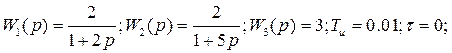
Введем следующие обозначения:

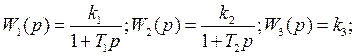
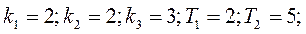
Осуществим преобразование структурной схемы:

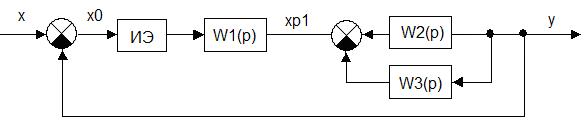
Рис.3. Преобразование структурной схемы.

Представим структурную схему данной ИСАУ в типовом виде:

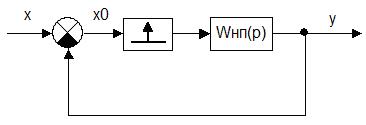
Рис.4. Представление структурной схемы в типовой форме.

Запишем выражение для 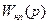в общем виде:

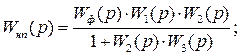
Выполним необходимые преобразования и запишем результат:

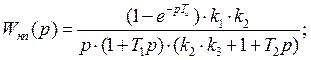
Таким образом, мы получили выражение для непрерывной приведенной части ИСАУ.

2. Нахождение по 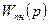дискретной передаточной функции разомкнутой импульсной системы .

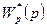Для того, чтобы получить передаточную функцию разомкнутой импульсной системы, сначала выполним разложение функции 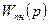на простые дроби:

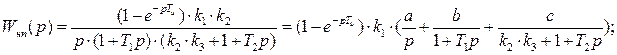
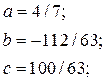
Применим дискретное преобразование Лапласа к полученному выражению для :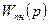

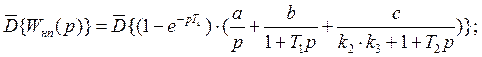
Вынесем выражение 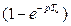за оператор дискретного преобразования Лапласа по свойству умножения преобразуемой функции на экспоненту:

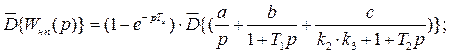
Воспользуемся свойством линейности дискретного преобразования Лапласа:

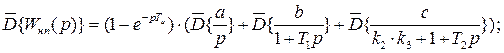
Используем таблицу для осуществления дискретного преобразования Лапласа:

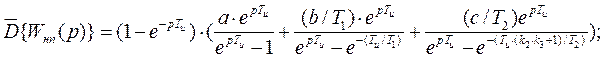
Далее выполним математические преобразования и получим следующее выражение для дискретной передаточной функции:

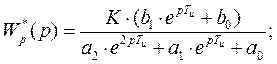
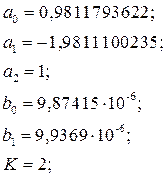
Запишем выражение для дискретной передаточной функции разомкнутой системы с подстановкой параметров:

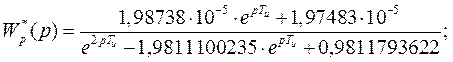
Таким образом, мы получили выражение для дискретной передаточной функции разомкнутой системы.

Построение годографа разомкнутой ИСАУ.

Построим годограф импульсной разомкнутой системы двумя способами:

1. по найденной ранее дискретной передаточной функции :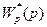

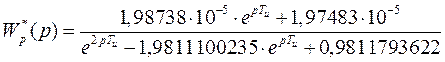
2. приближенным способом:

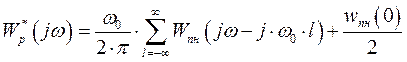
Рассмотрим данную формулу в приближении:

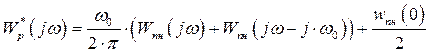где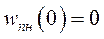

Для построения годографов воспользуемся математическим пакетом Mathcad 11 Enterprise Edition.

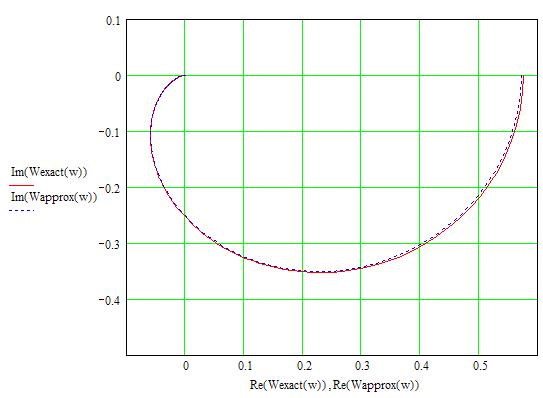
Рис.5. Годографы, построенные по дискретной передаточной функции (Wexact) и приближенным способом (Wapprox).

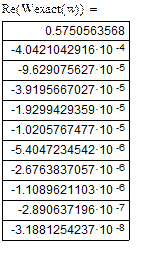Приведем таблицу значений для дискретной передаточной функции:

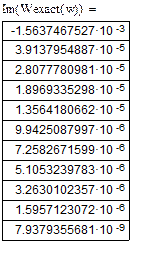Табл.1. Значения дискретной передаточной функции.

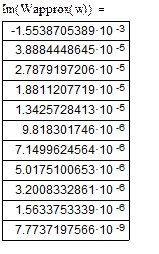
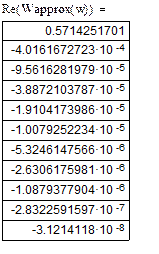
Приведем таблицу значений для функции, полученной по приближенной формуле:

Табл.2. Значения для функции, полученной по приближенной формуле.

Как мы можем увидеть из графиков и таблиц, годографы, построенные по точной и приближенной формулам, практически совпадают.