ПЗ 8. Решение задач линейного программирования. Геометрический метод решения задач линейного программирования
Рассмотрим основную задачу линейного программирования. Она состоит в определении максимального значения функции 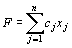 при условиях
при условиях 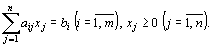
Перепишем эту задачу в векторной форме: найти максимум функции
F=CX (15)
при условиях
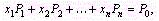 (16)
(16)
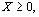 (17)
(17)
где 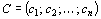 ,
, 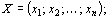 CX – скалярное произведение;
CX – скалярное произведение; 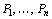 и
и 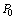 – m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы уравнений задачи:
– m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы уравнений задачи:
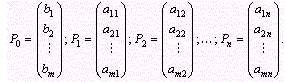
Определение 7.
План 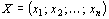 называется опорным планом, основной задачи линейного программирования, если система векторов
называется опорным планом, основной задачи линейного программирования, если система векторов 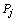 , входящих в разложение (16) с положительными коэффициентами
, входящих в разложение (16) с положительными коэффициентами 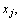 линейно независима.
линейно независима.
Так как векторы 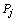 являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем т.
являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем т.
Определение 8.
Опорный план называется невырожденным, если он содержит ровно т положительных компонент, в противном случае он называется вырожденным.
Свойства основной задачи линейного программирования (15) – (17) тесным образом связаны со свойствами выпуклых множеств.
Определение 9.
Пусть 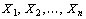 – произвольные точки евклидова пространства
– произвольные точки евклидова пространства 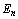 . Выпуклой линейной комбинацией этих точек называется сумма
. Выпуклой линейной комбинацией этих точек называется сумма 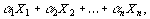 где
где 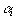 – произвольные неотрицательные числа, сумма которых равна 1:
– произвольные неотрицательные числа, сумма которых равна 1: 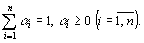
Определение 10.
Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и их произвольную выпуклую линейную комбинацию.
Определение 11.
Точка Х выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества.
Теорема 1.
Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто).
Определение 12.
Непустое множество планов основной задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.
Теорема 2.
Если основная задача линейного программирования имеет оптимальный план, то максимальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное значение целевая функция задачи принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.
Теорема 3.
Если система векторов 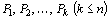 в разложении (16) линейно независима и такова, что
в разложении (16) линейно независима и такова, что
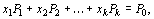 (18)
(18)
где все 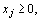 то точка
то точка 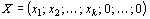 является вершиной многогранника решений.
является вершиной многогранника решений.
Теорема 4.
Если 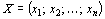 – вершина многогранника решений, то векторы
– вершина многогранника решений, то векторы 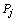 , соответствующие положительным
, соответствующие положительным 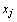 в разложении (16), линейно независимы.
в разложении (16), линейно независимы.
Сформулированные теоремы позволяют сделать следующие выводы.
Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т. е. для одного из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Если максимальное значение функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.
Вершину многогранника решений, в которой целевая функция принимает максимальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более двух переменных или задача, записанная в форме основной, содержит не более двух свободных переменных, т. е. 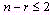 , где n – число переменных, r – ранг матрицы, составленной из коэффициентов в системе ограничений задачи.
, где n – число переменных, r – ранг матрицы, составленной из коэффициентов в системе ограничений задачи.
Найдем решение задачи, состоящей в определении максимального значения функции
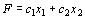 (19)
(19)
при условиях
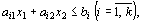 (20)
(20)
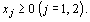 (21)
(21)
Каждое из неравенств (20), (21) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми 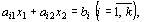
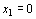 и
и 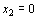 . В том случае, если система неравенств (20), (21) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых решений задачи (19) – (21) является выпуклое множество, которое называется многоугольником решений (введенный ранее термин “многогранник решений” обычно употребляется, если
. В том случае, если система неравенств (20), (21) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых решений задачи (19) – (21) является выпуклое множество, которое называется многоугольником решений (введенный ранее термин “многогранник решений” обычно употребляется, если 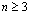 ). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция F принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня 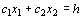 (где h – некоторая постоянная), проходящую через многоугольник решений, и будем передвигать ее в направлении вектора
(где h – некоторая постоянная), проходящую через многоугольник решений, и будем передвигать ее в направлении вектора 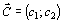 до тех пор, пока она не пройдет через ее последнюю общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
до тех пор, пока она не пройдет через ее последнюю общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
Отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня 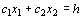 передвигается не в направлении вектора
передвигается не в направлении вектора 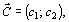 а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Итак, нахождение решения задачи линейного программирования (19) – (21) на основе ее геометрической интерпретации включает следующие этапы:
1. Строят прямые, уравнения которых получаются в результате замены в ограничениях (20) и (21) знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений.
4. Строят вектор 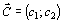 .
.
5. Строят прямую 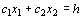 , проходящую через многоугольник решений.
, проходящую через многоугольник решений.
6. Передвигают прямую 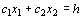 в направлении вектора
в направлении вектора 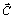 , в результате чего-либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.
, в результате чего-либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.
7. Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.
