Определение. Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию
Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими.
Рассмотрим уравнение вида 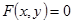 . Покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси
. Покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси 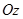 . Пусть
. Пусть 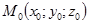 - некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная
- некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная 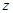 , ему будут удовлетворять координаты всех точек
, ему будут удовлетворять координаты всех точек 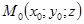 , где
, где 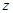 - любое число. Следовательно, при любом
- любое число. Следовательно, при любом 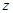 точка
точка 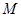 лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку
лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку 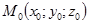 параллельно оси
параллельно оси 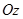 . А это означает, что поверхность, определяемая уравнением, составлена из прямых, параллельных оси
. А это означает, что поверхность, определяемая уравнением, составлена из прямых, параллельных оси 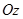 , то есть она является цилиндрической поверхностью.
, то есть она является цилиндрической поверхностью.
Заметим, что на плоскости 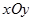 уравнение определяет направляющую рассматриваемой цилиндрической поверхности.
уравнение определяет направляющую рассматриваемой цилиндрической поверхности.
Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.
Нас будут интересовать только те цилиндрические поверхности, которые являются поверхностями второго порядка.
