Контрольная расчетная работа по кинематике
Задача 2.1
Задача 2.1 относится к кинематике точки, способ задания движения координатный. Для определения скорости и ускорения точки следует найти их проекции на координатные оси. Используя найденные значения скорости и ускорения, можно определить касательное и нормальное ускорения точки, а также радиус кривизны траектории. Исходные данные приведены в табл. 5.
Таблица 5
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | |
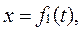 см см | 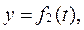 см см | 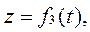 см см | 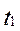 , см , см | |
| t3+1 | sinpt | sin2pt | ||
| 2t2–2 | cospt | cos2pt | ||
| 3t4–3 | sinpt/2 | sin2pt/2 | ||
| t3–4 | cospt/2 | cos2pt/2 | ||
| 3t2+5 | sinpt/3 | sin2pt/3 | ||
| 4t-6 | cospt/3 | cos2pt/3 | ||
| t3+7 | sinpt/4 | sin2pt/4 | ||
| 4t2–8 | cospt/4 | cos2pt/4 | ||
| 5t+9 | sinpt/6 | sin2pt/6 | ||
| t2+10 | cospt/6 | cos2pt/6 |
Условия
Движение точки задано уравнениями в декартовых координатах 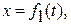
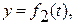
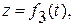 (x, y, z в см, t в с). Определить величину и направление скорости и ускорения точки, а также радиус кривизны траектории в момент времени
(x, y, z в см, t в с). Определить величину и направление скорости и ускорения точки, а также радиус кривизны траектории в момент времени 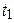 , см.
, см.
Пример решения задачи 2.1
Условие. Решим задачу в случае, если уравнения движения точки в декартовых координатах имеют вид:
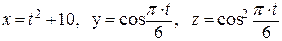
(для момента времени 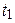 = 1 c).
= 1 c).
Решение. 1. Определим проекции скорости на оси декартовых координат в указанный момент времени:
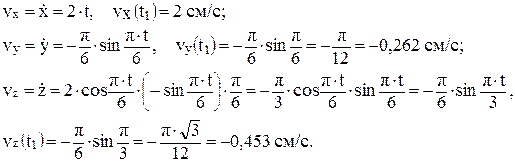
2. Модуль скорости точки в указанный момент времени:
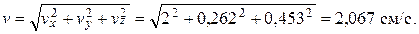
3. Направление вектора скорости в данный момент времени определим с помощью направляющих косинусов:
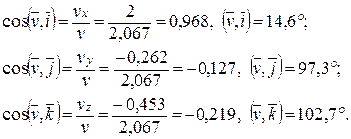
4. Определим проекции ускорения на оси декартовых координат в указанный момент времени:
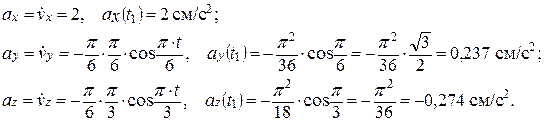
5. Модуль ускорения точки в указанный момент времени:
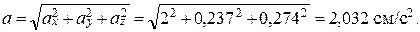
6. Направление вектора ускорения в данный момент времени определим с помощью направляющих косинусов:
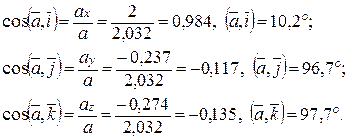
7. Найдем модуль проекции ускорения точки на касательную (модуль касательного ускорения точки) через значения проекций скорости и ускорения на оси координат: 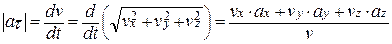 .
.
Для заданного момента времени t1
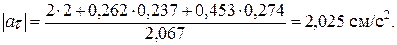
8. Модуль проекции ускорения точки на нормаль (нормальное ускорение) точки найдем из соотношения 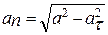 . Для заданного момента времени t1
. Для заданного момента времени t1

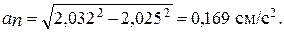
9. Радиус кривизны траектории r найдем из формулы для нормального ускорения точки 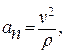 откуда
откуда 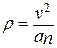 . В нашем случае
. В нашем случае
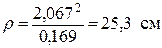 .
.
Задача 2.2
Задача 2.2 посвящена одному из простейших движений твердого тела – вращению твердого тела вокруг неподвижной оси. Исходные данные для различных вариантов приведены в табл. 6.
Таблица 6
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | ||||||
| t1, с | t2, c | t3, c | h, см | Номер условия | j=j(t), рад | w1, с-1 | w2, с-1 | e, с-2 | |
| 0,5 | 2.2.1 | t3+sin(pt) | – | – | – | ||||
| 1,0 | 2.2.1 | 2t2–cos(pt) | – | – | – | ||||
| 1,5 | 2.2.1 | 3t+sin2(pt/2) | – | – | – | ||||
| 2,0 | 2.2.1 | 4t–cos2(pt/2) | – | – | – | ||||
| 2,5 | 2.2.2 | – | – | ||||||
| 0,5 | 2.2.2 | – | – | ||||||
| 1,0 | 2.2.2 | – | – | ||||||
| 1,5 | 2.2.3 | – | – | 1,0 | |||||
| 2,0 | 2.2.3 | – | – | 1,5 | |||||
| 2,5 | 2.2.3 | – | – | 2,0 |
Условия
2.2.1. По заданному уравнению вращательного движения твердого тела вокруг неподвижной оси j= j (t) определить: 1) угловую скорость и угловое ускорение тела в момент времени t1; 2) скорость и ускорение точки тела, отстоящей на расстоянии h от оси в момент t2; 3) число оборотов N тела за время t3.
2.2.2. Диск, вращающийся равноускоренно вокруг неподвижной оси, в моменты времени t1 и t2 имеет угловые скорости w1 и w2 соответственно. Определить: 1) скорость и ускорение точки, отстоящей на расстоянии h от оси, в момент t2; 2) число оборотов N тела за время t3; 3) уравнение вращательного движения диска, если в начальный момент времени t0=0 начальный угол поворота j0=0.
2.2.3. Тело, вращаясь равноускоренно с угловым ускорением e, имеет в момент времени t1 угловую скорость w1. Определить: 1) скорость и ускорение точки тела, отстоящей на расстоянии h от оси в момент t2; 2) число оборотов N тела за время t3; 3) уравнение вращательного движения тела, если в начальный момент времени t0=0 начальный угол поворота j0=0.
Пример решения задачи 2.2
Условие. Тело, вращаясь равноускоренно с угловым ускорением e=2 рад/с, имеет в момент времени t1=2,5 с угловую скорость w1=40 рад/с. Определить: 1) скорость и ускорение точки тела, отстоящей на расстоянии h=55 см от оси вращения в момент t2=7 с; 2) число оборотов N тела за время t3=10 с; 3) уравнение вращательного движения тела, если в начальный момент времени t0=0 начальный угол поворота j0=0.
Решение. 1. При равноускоренном вращении угловая скорость тела изменяется по закону 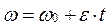 . Зная значение угловой скорости w1 в некоторый момент времени t1 и угловое ускорение e, можно найти начальную угловую скорость w0 (при t0=0):
. Зная значение угловой скорости w1 в некоторый момент времени t1 и угловое ускорение e, можно найти начальную угловую скорость w0 (при t0=0): 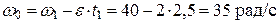 . Отсюда угловая скорость тела в момент времени t2=7 с будет равна
. Отсюда угловая скорость тела в момент времени t2=7 с будет равна 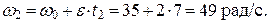
Скорость v и ускорение a точки М тела, отстоящей на расстоянии h=55 см от оси вращения, в момент времени t2 = 7 c будут равны:
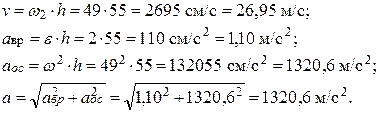
Направление векторов скорости и ускорений указаны на рис. 11.
2. Число оборотов тела за время t3=10 с определим по соотношению
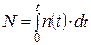 ,
,
где n (t) – число оборотов тела за секунду в данный момент времени.
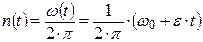
В рассматриваемой задаче
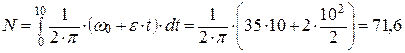 об.
об.
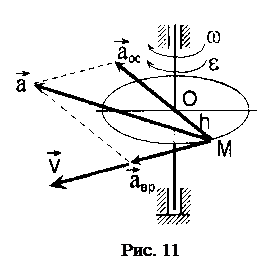
3. Уравнение вращательного движения тела 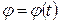 получим из соотношения
получим из соотношения 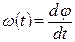 , умножив обе его части на дифференциал времени dt:
, умножив обе его части на дифференциал времени dt: 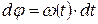 . Интегрируя полученное дифференциальное уравнение с учетом начальных условий (t0=0, j0=0):
. Интегрируя полученное дифференциальное уравнение с учетом начальных условий (t0=0, j0=0):
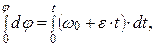
получим 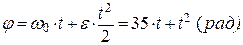
Задача 2.3
Данная задача относится к сложному движению точки. Для определения абсолютной скорости точки необходимо найти ее относительную и переносную скорости и воспользоваться теоремой параллелограмма скоростей. Исходные данные представлены в табл. 7.
Таблица 7
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | ||||
| AM=s=¦(t), см | t1, c | w, c-1 |  R, см R, см | a, см | a, град | Номер схемы (рис. 12) | |
| 30sinpt/6 | – | ||||||
| 20(t2–t) | |||||||
| 25(1–cospt/4) | – | ||||||
| 3t2 | – | ||||||
| 40sinpt/3 | – | ||||||
| 90(cospt/4–1) | – | ||||||
| 15(t+sinpt/2) | – | ||||||
| 20(t–sinpt/6) | – | ||||||
| 2(t2+t) | |||||||
| 8(t+sinpt/3) | – | – |
Условие
Точка М движется по хорде диска (см. рис. 12, схемы 1, 3, 4), по диаметру (см. рис. 12, схемы 2, 5, 7, 8, 9) или ободу (см. рис. 12, схемы 6, 10) согласно закону s=АМ=¦(t). Диск вращается вокруг неподвижной оси, проходящей через точку О1 и перпендикулярной плоскости диска (см. рис. 12, схемы 1, 2, 6, 7, 9), или вокруг оси О1О2, лежащей в плоскости диска (см. рис. 12, схемы 3, 4, 5, 8, 10), в направлении, указанном стрелкой, с постоянной угловой скоростью w. Определить абсолютную скорость точки М в момент времени t1.
Примечание. Точка М изображена на схемах (см. рис. 12) в области положительных значений дуговой координаты s.
Пример решения задачи 2.3
Условие. Точка М движется по ободу диска радиусом R=20 см согласно закону s=АМ=6 t sin(pt/3). Диск вращается вокруг неподвижной оси О1О2, лежащей в плоскости диска, в направлении, указанном стрелкой, с постоянной
угловой скоростью w=0,5 рад/с. Определить абсолютную скорость точки М в момент времени t1=5 с (рис. 13).
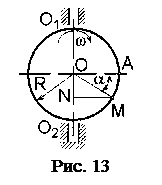 Решение. В данной задаче относительное движение точки – движение по ободу диска относительной системы отсчета, связанной с диском; переносное движение – вращение вместе с диском вокруг неподвижной оси; абсолютное движение – движение точки относительно неподвижной оси.
Решение. В данной задаче относительное движение точки – движение по ободу диска относительной системы отсчета, связанной с диском; переносное движение – вращение вместе с диском вокруг неподвижной оси; абсолютное движение – движение точки относительно неподвижной оси.
1. Определим параметры относительного движения точки:
а) положение точки М в заданный момент времени t=5 с:
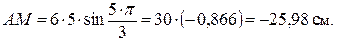
Знак минус означает, что точка М в рассматриваемый момент времени находится в области отрицательных значений дуговой координаты s;
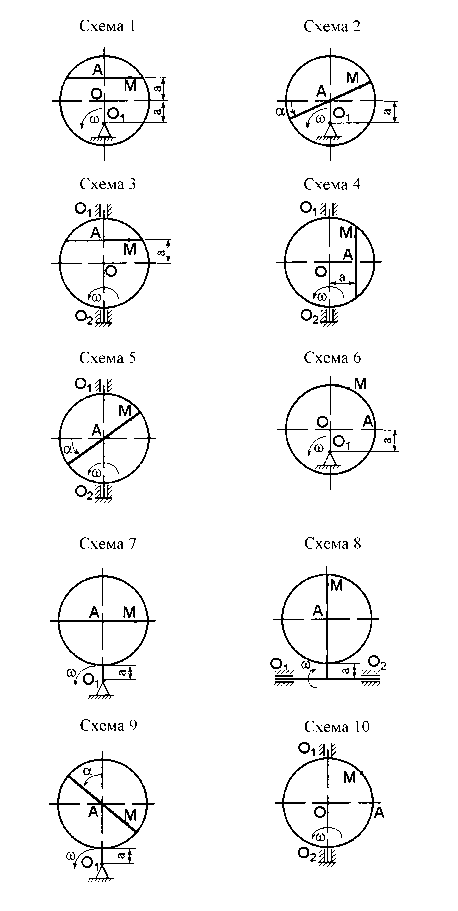
Рис. 12. Схемы к задаче 2.3
б) определим центральный угол a и отрезок MN: 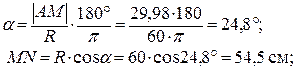
в) найдем проекцию относительной скорости 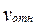 точки М на касательную в данный момент времени:
точки М на касательную в данный момент времени:
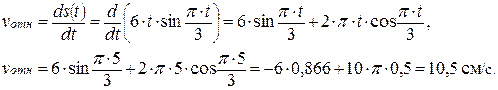
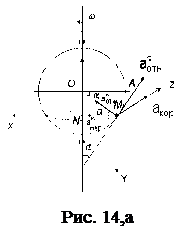
Вектор относительной скорости направлен по касательной к относительной траектории точки (по касательной к дуге АМ) в сторону возрастания дуговой координаты (рис. 14), так как проекция на касательную имеет положительное значение.
 2. Определим модуль переносной скорости точки М как вращательной скорости той точки диска, где в данное мгновение находится движущаяся точка М:
2. Определим модуль переносной скорости точки М как вращательной скорости той точки диска, где в данное мгновение находится движущаяся точка М:
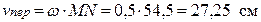 .
.
Вектор переносной скорости перпендикулярен плоскости диска и направлен в сторону его вращения.
3. Модуль абсолютной скорости точки М найдем по формуле 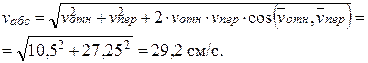
 Вектор абсолютной скорости направлен по диагонали прямоугольника, построенного на относительной и переносной скоростях как сторонах.
Вектор абсолютной скорости направлен по диагонали прямоугольника, построенного на относительной и переносной скоростях как сторонах.
4. Абсолютное ускорение  точки М равно геометрической сумме относительного
точки М равно геометрической сумме относительного  отн ,переносного
отн ,переносного 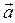 пер и кориолисова
пер и кориолисова 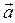 кор ускорений:
кор ускорений:
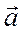 абс =
абс = 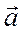 отн +
отн + 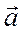 пер +
пер + 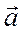 кор ,
кор ,
или с учетом условий задачи в развернутом виде
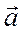 абс =
абс = 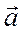
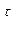 отн +
отн + 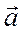
 отн +
отн + 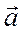
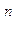 пер +
пер + 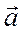 кор ,
кор ,
где при t1=5с касательное ускорение в относительном движении:
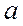
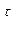 отн =
отн = 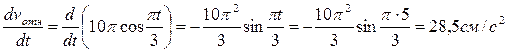 ;
;
нормативное ускорение в относительном движении:
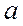
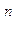 отн =
отн = 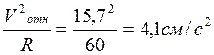 ;
;
нормативное ускорение в переносном движении:
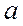
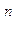 пер =
пер = 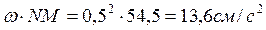 ;
;
кориолисово ускорение:
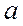 кор =
кор = 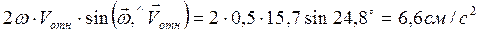 .
.
Положительный знак 
 отн показывает, что вектор
отн показывает, что вектор 
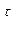 отн направлен в сторону положительных значений S; вектор
отн направлен в сторону положительных значений S; вектор 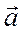
 отн направлен по нормали к траектории движения точки в относительном движении, т.е. по нормали к окружности радиусом MN к её центру, вектор
отн направлен по нормали к траектории движения точки в относительном движении, т.е. по нормали к окружности радиусом MN к её центру, вектор 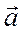 кор направлен согласно правилу векторного произведения векторов
кор направлен согласно правилу векторного произведения векторов 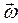 и
и 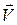 отн (рис. 14,а)
отн (рис. 14,а)
Модуль абсолютного ускорения точки М находим способом проекции на оси х, у и z (рис. 14,б):
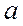 абс x =
абс x = 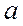
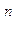 пер+
пер+ 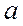
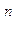 отн cos
отн cos 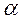 -
- 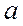
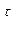 отн sin
отн sin 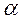 =13,6 + 4,1cos 24,8
=13,6 + 4,1cos 24,8  – - sin 24,8
– - sin 24,8  = 5,37 см/с2
= 5,37 см/с2
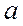 абс y = -
абс y = - 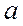
 отн sin
отн sin 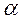 -
- 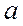
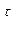 отн cos
отн cos 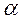 = 4,1sin 24,8
= 4,1sin 24,8  – 28,5cos24,8
– 28,5cos24,8  = = -27,6 см/с2
= = -27,6 см/с2
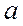 абс z =
абс z = 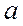 кор = 6,6 см/с2
кор = 6,6 см/с2
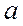 абс =
абс = 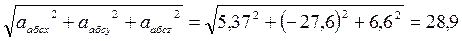 см/с2
см/с2
Направление вектора 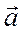 абс определяется её углами с осями координат:
абс определяется её углами с осями координат:
( 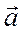 абс ^,
абс ^, 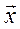 ) = абс cos
) = абс cos 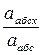 = абс cos
= абс cos 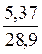 = 79,3
= 79,3 
( 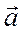 абс ^,
абс ^, 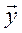 ) = абс cos
) = абс cos 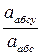 = абс cos
= абс cos 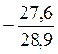 = 162,7
= 162,7 
( 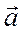 абс ^,
абс ^, 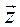 ) = абс cos
) = абс cos 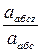 = абс cos
= абс cos 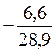 = 76,8
= 76,8 
Задача 2.4
Задача 2.4 относится к плоскому движению твердого тела. Скорость ползуна для данного положения механизма можно вычислить с помощью как теоремы о проекциях скоростей двух точек тела, так и мгновенного центра скоростей шатуна. Для этого необходимо знать скорость какой-нибудь точки шатуна (например точки А) и направление скорости ползуна.
Ускорение ползуна в данный момент времени можно найти с помощью векторной формулы распределения ускорений точек плоской фигуры, спроектировав ее на два взаимно перпендикулярных направления. В качестве полюса удобно принять точку А. Исходные данные к задаче даны в табл. 8.
Условие
Кривошип ОА длиной R вращается вокруг неподвижной оси О с постоянной угловой скоростью w и приводит в движение шатун АВ длиной L и
Таблица 8
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | |||
| R, см | L, cм | a, град |  b, град b, град | w, c-1 | Номер схемы (рис. 15) | |
ползун В. Для заданного положения механизма найти скорость и ускорение ползуна В.
Примечание. Если при заданных значениях углов окажется, что шатун АВ перпендикулярен направляющим ползуна (см. рис. 15, схемы 1, 6), то значение угла b следует принять равным 15°.
Пример решения задачи 2.4
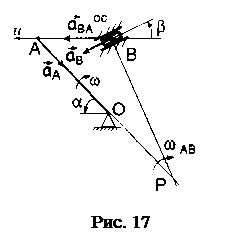
Условие. Кривошип ОА длиной R=64 см вращается вокруг неподвижной оси О с постоянной угловой скоростью w=1 рад/с и приводит в движение шатун АВ длиной L=72 см и ползун В. Для положения механизма, заданного значениями углов a=45°, b=30,° найти скорость и ускорение ползуна В. Схема механизма приведена на рис. 16. мгновенным центром скоростей Р (см. рис. 16).
Рассмотрим движение шатуна в данный момент времени как вращательное относительно оси,
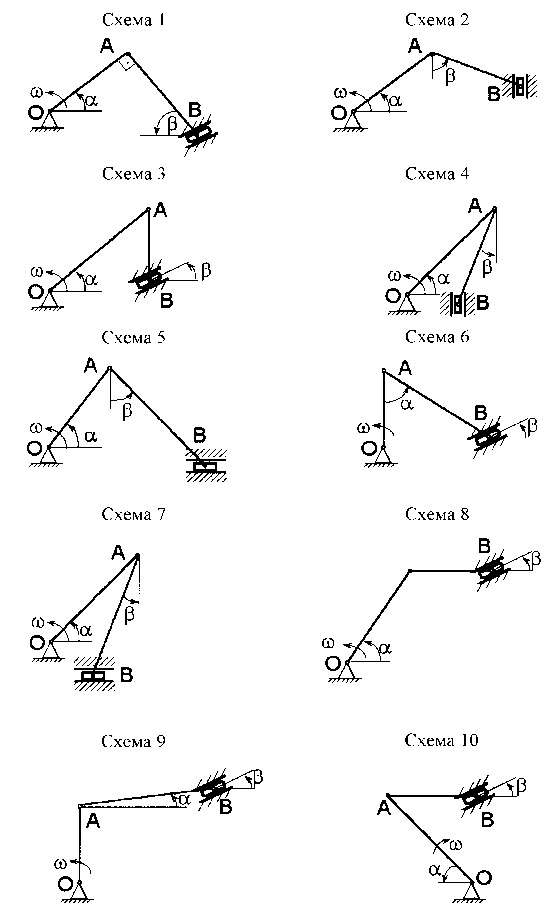
Рис. 15. Схемы к задаче 2.4
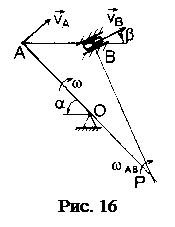 проходящей через мгновенный центр скоростей Р перпендикулярно неподвижной плоскости, по отношению к которой происходит плоское движение. Угловая скорость шатуна в этом случае определяется из соотношения
проходящей через мгновенный центр скоростей Р перпендикулярно неподвижной плоскости, по отношению к которой происходит плоское движение. Угловая скорость шатуна в этом случае определяется из соотношения 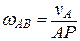 , а скорость ползуна В как вращательная – из соотношения
, а скорость ползуна В как вращательная – из соотношения 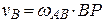 .
.
Расстояния АР и BP определим из решения треугольника АВР, применив теорему синусов. Для заданного положения механизма получим
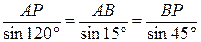 , откуда
, откуда
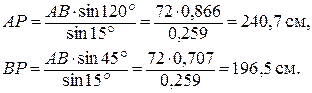
Подставив найденные значения расстояний в соответствующие формулы, получим 
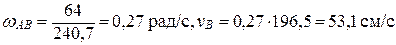 . Направления скоростей показаны на рис. 16.
. Направления скоростей показаны на рис. 16.
2. Для определения ускорения ползуна B воспользуемся векторным равенством:
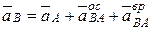 , (1)
, (1)
где 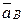 – ускорение ползуна В;
– ускорение ползуна В;
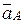 – ускорение точки А, выбранной за полюс;
– ускорение точки А, выбранной за полюс;
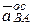 – осестремительное (центростремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;
– осестремительное (центростремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;
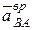 – вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А.
– вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А.
Ускорение точки А кривошипа при равномерном вращении вокруг неподвижной оси О состоит только из осестремительной составляющей, модуль которой определяется формулой 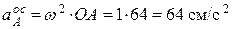 . Вектор ускорения точки А направлен к оси вращения (рис. 17),
. Вектор ускорения точки А направлен к оси вращения (рис. 17), 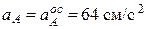 .
.
Осестремительное ускорение точки В при ее вращении вокруг полюса А:
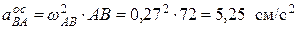 .
.
 Рассчитать вращательное ускорение
Рассчитать вращательное ускорение 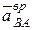 обычным способом не представляется возможным, так как величина углового ускорения звена АВ неизвестна. Несмотря на это обстоятельство, векторное равенство (1) позволяет найти ускорение ползуна В. Для этого воспользуемся тем, что нам известно направления вектора
обычным способом не представляется возможным, так как величина углового ускорения звена АВ неизвестна. Несмотря на это обстоятельство, векторное равенство (1) позволяет найти ускорение ползуна В. Для этого воспользуемся тем, что нам известно направления вектора 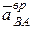 (он перпендикулярен ускорению
(он перпендикулярен ускорению 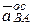 ) и вектора ускорения искомого ускорения
) и вектора ускорения искомого ускорения 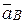 (вдоль прямолинейной траектории точки В).
(вдоль прямолинейной траектории точки В).
Проведем вектор ускорения 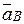 точки В, предполагая, что он направлен противоположно скорости точки В. Спроектируем векторное равенство (1) на ось u, перпендикулярную ускорению
точки В, предполагая, что он направлен противоположно скорости точки В. Спроектируем векторное равенство (1) на ось u, перпендикулярную ускорению 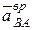 и проходящую через точки А и В, получим
и проходящую через точки А и В, получим
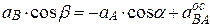 .
.
Отсюда
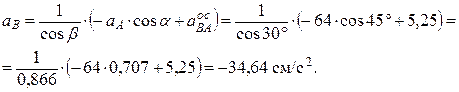
Знак минус показывает, что истинное направление ускорения точки В противоположно принятому.
