Ii. экспериментальная часть

СПЕКТРАЛЬНЫЙ АНАЛИЗ ГАРМОНИЧЕСКИХ СИГНАЛОВ. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ

Цель работы: изучение основных свойств преобразования Фурье.

I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Гармонический сигнал — это гармонические колебания, которые описываются уравнением:

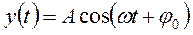, (1)

где 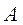— амплитуда сигнала;

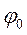— начальная фаза гармонического сигнала;

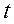— время;

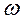— циклическая частота сигнала;

Модуляция — это процесс изменения одного или нескольких параметров высокочастотного несущего колебания по закону низкочастотного информационного сигнала (сообщения).

В случае гармонического несущего колебания, определяемого выражением (1) различают три вида модуляции (по всем трем параметрам):

– амплитудная;

– частотная;

– фазовая.

Из них наиболее просто реализуемая – амплитудная, которая описывается уравнением:

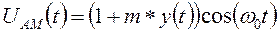, (2)

где 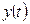– модулирующий (информационный) сигнал, ;

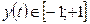m – глубина модуляции;

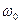– несущая частота (циклическая).

II. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

1. Создать среду для моделирования преобразования Фурье. Для этого необходимо задать частоту дискретизации Fs и длительность сигнала (число отсчётов) L. Для наглядности частота дискретизации должная значительно превышать частоты исследуемых гармонических сигналов (в 5–10 раз минимум), а длительность составлять не менее 1000 отсчетов. Чем больше число отсчётов, тем точнее просчитывается спектр, однако тем больше времени требуется программе на вычисления.

2. Промоделировать следующие сигналы:

2.1. Два гармонических сигнала (сигнал 1 и сигнал 2) с амплитудами А1 и А2 соответственно и частотами f₁ и f₂ заданными в таблице 1 в зависимости от номера бригады;

2.2. Сумму сигналов 1 и 2 (сигнал 3);

2.3. Произведение сигналов 1 и 2 (сигнал 4);

2.4. Три амплитудно-модулированных колебания (сигналы 5 – 7), модулирующими сигналом которого являются сигналы 1 – 3 соответственно. Несущая частота f₀ и глубина модуляции m заданы в таблице 1.

2.5. Произвольно изменить несущую частоту и глубину модуляции в небольших пределах от заданных величин и получить амплитудно-модулированное колебание, модулирующим сигналом которого является сигнал 3.

3. Вычислить спектры сигналов 1 – 8. Для вычисления можно использовать код, приведенный в листинге ниже. После выполнения данного кода будет сформирован вектор амплитуд А и соответствующий ему вектор частот f, по которым можно построить спектр, использую функцию plot либо stem.

% Вычисление спектра сигнала

NFFT = 2^nextpow2(L); % Число точек преобразования Фурье

Y = fft(y,NFFT)/L; % Преобразование Фурье

f = Fs/2*linspace(0,1,NFFT/2); % Частотный вектор

A = 2*abs(Y(1:NFFT/2)); % Амплитудный спектр сигнала

4. Построить все сигналы и соответствующие спектры.

5. Сделать выводы о характере получившихся спектров, а также выявить связь параметров спектра с параметрами сигнала.

6. Написать отчет по работе.

Содержание отчета:

1. Титульный лист с указанием на нем номера бригады;

2. Цель работы и задание (параметры сигналов);

3. Теоретические сведения;

4. Листинг программы;

5. Результаты работы программы;

6. Нетривиальные выводы в соответствии с п. 5 экспериментальной части.

Таблица 1 – Варианты задания

Бригада	А1	А2	f1, Гц	f2, Гц	f0, Гц	m
	0.2	0.4				0.5
		0.5
						0.25
	0.5	0.5				0.35
	0.5					0.8
	0.2	0.5				0.1
	0.2	0.8				0.5
	0.35	0.7
	0.6	0.8				0.25
		0.8				0.35
	0.25	0.75				0.8
		0.25				0.1