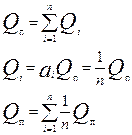Б. Численное решение задачи

Для численного решения задачи определения оптимальной цены и партии изделий требуется построить график зависимости прибыли S от размера партии Q по формуле (1).

Оптимальные значения количества изделий Q_m и цены C_m соответствуют точке максимума на графике прибыли S(Q).

Задача 2. Оптимальная стратегия продажи заданной партии товара

Рыночная практика показывает, что большую партию товара обычно продают по частям, начиная с высокой цены и постепенно снижая цену по мере насыщения рынка и уменьшения спроса.

В этой задаче считается заданным размер партии товара Q_п = Q_m, который необходимо продать так, чтобы получить максимальную прибыль. Функции спроса (2) и удельных издержек (3) остаются неизменными из задачи 1.

В данной работе, для простоты всю партию товара Q_п разделим надве части Q₁ и Q₂ (рис.1):

Q_п = Q₁ + Q₂ , (7)

которые продаются в два приема по ценам C₁ и C₂ . Требуется определить оптимальные размеры частей Q₁ и Q₂ и их цены C₁ и C₂ , обеспечивающие максимальный размер получаемой в результате продажи суммарной прибыли S. Задачу требуется решить аналитическим и численным методами.

А. Аналитическое решение задачи.

В данной задаче общая прибыль S складывается из прибылей S₁ и S₂, полученных от продажи двух частей партии товара. При расчетах будем считать, что удельные затраты C_eп зависят только от размера партии товара Q_п и не зависят от размера частей партии.

S = S₁(Q₁ , C₁)+ S₂ (Q₂ , C₂ ) = Q₁ C₁ + (Q_п – Q₁ ) C₂ – C_eп Q_п = . . . (8)

Записывая необходимое условие максимума прибыли dS / dQ₁=0 определим оптимальное значение части партии Q_1m. Затем, по формулам (7) и (2) найдем оптимальные значения Q_2m , C_1m и C_2m .

Сравнить полученное значение прибыли в задаче 2 с прибылью, рассчитанной в задаче 1.

Б. Численное решение задачи.

Для численного решения поставленной задачи требуется построить график зависимости прибыли S от размера части партии Q₁ по формуле (8). Для этого необходимо заполнить табл.1, в которой следует изменять значение Q₁ от 0 до Q_п . Из графика и таблицы определить Q₁, Q₂, C₁, C₂, обеспечивающие максимум доход Д и прибыли S.

Таблица 1

Q1						Qп
C1	Cd1					С2
Q2=Qп-Q1	Qп
Д=Q1C1+Q2C2
S=Д-CепQп	Sm					Sm

РЕШЕНИЕ

Задача 1.

Аналитическое решение:

1. C_d=12-2Q

C_e=3+0,5/Q

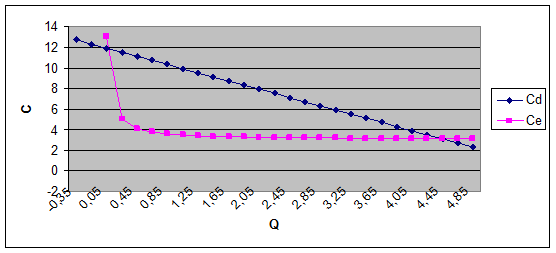
Рис.2 Кривая спроса и кривая удельных издержек.

Определим Q_1б/у и Q_2б/у, для этого

12-2Q=3+0,5/Q

2Q²-9Q+0,5=0

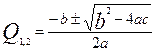
Q_1б/у=0,05

Q_2б/у=4,44

2. Определим оптимальное количество изделий (Q_m) и оптимальную цену (C_m) по формулам (5) и (6):

Q_m=0,5*(12-3)/2=2,25

C_m=0,5*(12+3)=7,5

Определим максимальную прибыль (S_m), для этого подставим Q=Q_m в формулу (4). S_m это максимальная прибыль, если всю партию товара Q_m продать по цене C_m за штуку.

S_m=(12-3-2*2,25)*2,25-0,5=9,625

Численное решение:

Построим график зависимости прибыли S от размера партии Q по формуле (1). Оптимальное значение количества изделий Q_m и цены C_m соответствуют точке максимума на графике прибыли S(Q).

Q	0,05	0,25	0,45	0,65	0,85	1,05	1,25	1,45	1,65	1,85	2,05	2,25
S	-0,06	1,63	3,15	4,51	5,71	6,75	7,63	8,35	8,91	9,31	9,55	9,63

Q	2,45	2,65	2,85	3,05	3,25	3,45	3,65	3,85	4,05	4,25	4,45
S	9,55	9,31	8,91	8,35	7,63	6,75	5,71	4,51	3,15	1,63	-0,06

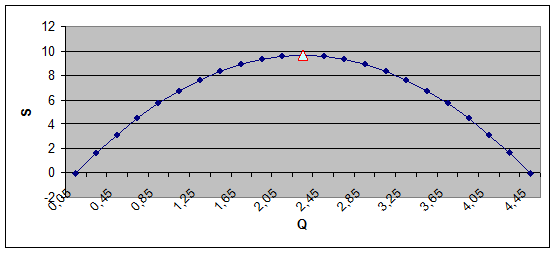
Рис.3 График зависимости прибыли S от размера партии Q.

При оптимальном количестве изделий 2,25 получаем максимальную прибыль 9,625, при цене изделия 7,5.

Задача 2.

Аналитическое решение:

В данной задаче общая прибыль S складывается из прибылей S₁ и S₂, полученных от продажи двух частей партии товара. Удельные затраты С_еп зависят только от размера партии товара Q_п и не зависят от размера частей партии.

S=S₁(Q₁,C₁)+S₂(Q₂,C₂)=Q₁C₁+(Q_п-Q₁)C₂-C_епQ_п= Q₁C₁+Q_п C₂-Q₁C₂-C_епQ_п=

=Q₁(C_d1-C_d2Q₁)+(Q_п-Q₁)(C_d1-C_d2(Q_п-Q₁))- C_епQ_п=

=С_d1Q₁-C_d2Q₁²+C_d1(Q_п-Q₁)-C_d2(Q_п-Q₁)² - C_епQ_п;

Из необходимого условия максимума dS/dQ₁=0 определим оптимальное значение части партии Q_1m.

dS/dQ₁ = (С_d1Q₁-C_d2Q₁²+C_d1(Q_п-Q₁)-C_d2(Q_п-Q₁)² - C_епQ_п)̍ =

= С_d1-2 C_d2Q₁- C_d1-2 C_d2(Q_п-Q₁)*(-1)-0= С_d1-2 C_d2Q₁- C_d1+2 C_d2(Q_п-Q₁);

С_d1-2 C_d2Q₁- C_d1+2 C_d2(Q_п-Q₁)=0;

-Q₁+ Q_п-Q₁=0;

Q_1m=Q_п/2;

Q_1m=2,25/2=1,125;

Определим оптимальное значение Q_2m по формуле (7).

Q_2m= Q_п- Q_1m=2,25-1,125=1,125;

По формуле (2) определим оптимальное значение С_1m и C_2m.

С_1m=С_d1-C_d2Q_1m=12-2*1,125=9,75;

С_2m=С_d1-C_d2Q_п=12-2*2,25=7,5;

Найдем общую прибыль S по формуле (8).

S=S₁+S₂=Q_1mC_1m+Q_2mC_2m-(C_e1+C_e2/Q_п)Q_п=12,16;

Прибыль в первой задаче равна 9,625, прибыль во второй задаче равна 12,16. Следовательно, выгодно разбить партию на 2 части и продавать первую часть по цене C_1m, вторую часть по цене C_2m, при этом получим максимальную прибыль.

Численное решение:

Q_п=Q_m=2,25;

C_еп=С_е1+С_е2/Q_п=3+0,5/2,25=3,22;

С₂=С_d1-C_d2Q_п=12-2*2,25=7,5;

Q1		0,225	0,45	0,675	0,9	1,125	1,35	1,575	1,8	2,025	2,25
C1		11,55	11,1	10,65	10,2	9,75	9,3	8,85	8,4	7,95	7,5
Q2=Qп-Q1	2,25	2,025	1,8	1,575	1,35	1,125	0,9	0,675	0,45	0,225
Д=Q1C1+Q2C2	16,9	17,8	18,5	19,0	19,3	19,4	19,3	19,0	18,5	17,8	16,9
S=Д-CепQп	9,63	10,54	11,25	11,76	12,06	12,16	12,06	11,76	11,25	10,54	9,63

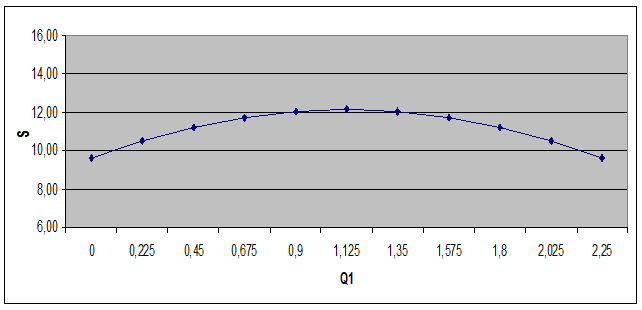
Рис.4 График зависимости прибыли S от размера части партии Q₁

Задача 3 (дополнительное задание).

Аналитическое решение:

Получим аналитическое решение для расчета оптимальных размеров Q_i для общего случая деления партии товара на n частей, причем .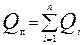

Заменим Q_i на произведение a_iQ_п, где a_i – коэффициент, на который нужно умножить Q_п, чтобы получить Q_i. 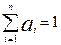, тогда коэффициент a_n можно выразить через a_i 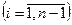a_n=(1- )

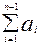Запишем общую прибыль S, которая складывается из прибылей S₁, S₂,…, S_n, полученных от продажи n частей партии товара.

S=S₁+S₂+ … +S_n;

При расчетах будем считать, что удельные затраты С_еп зависят только от размера партии товара Q_п и не зависят от размера частей партии.

S=a₁Q_п(C_d1 – C_d2Q_пa₁) + a₂Q_п(C_d1 – C_d2Q_пa₂) + … + (1- 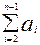) Q_п *

*(C_d1 – C_d2Q_п (1 – 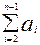)) – C_епQ_п (1)

Далее из необходимого условия максимума прибыли dS/da_i=0 определим оптимальные значения коэффициентов a_i, для этого решим систему уравнений:

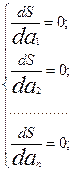
После того как возьмем производную, останутся те члены, где содержится элемент, по которому берем производную.

Рассмотрим уравнение

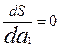(2)

В (1) от a₁ зависят слагаемые Cd₁Q_пa_i; Cd₂Q_п²a₁² ; Cd₂Q_п²(1- 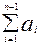), т.е.

S=a₁Q_п(C_d1 – C_d2Q_пa₁) + a₂Q_п(C_d1 – C_d2Q_пa₂) + … + (1- a₁ - 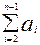) Q_п *

*(C_d1 – C_d2Q_п (1 – a₁ - 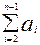)) – C_епQ_п =

=C_d1Q_пa₁ – C_d2Q_п²a₁² + C_d1Q_пa₂ – C_d2Q_п²a₂² +…+ C_d1Q_п – C_d1Q_пa₁ – C_d1Q_п -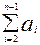

- C_d2Q_п²(1 – a₁ - 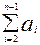)² – C_епQ_п;

Введем обозначение D – сумма всех коэффициентов a_i (i= )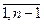

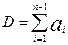(3)

Для того чтобы выделить из a_n ту часть, которая зависит от a_i, введем обозначение L_i – сумма всех коэффициентов a_i, кроме коэффициента, по которому берем производную, например L₁= 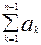-a₁

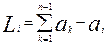, (4)

D=L_i + a_i

Запишем общий случай нахождения производной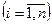

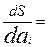(C_d1Q_пa_i - C_d2Q_п²a_i² + C_d1Q_п - C_d1Q_пa_i - C_d1Q_пL_i -C_d2Q_п²(1 – a_i -L_i)² - C_епQ_п)̍ =0;

C_d1Q_п - 2C_d2Q_п²a_i + 0 - C_d1Q_п - 0 + 2C_d2Q_п²(1 – a_i -L_i) =0;

-a_i + 1 - a_i - L_i=0;

2a_i=1-L_i;

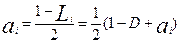; (5)

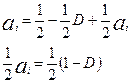
a_i=1-D (6)

Найдем D из (3) и (4):

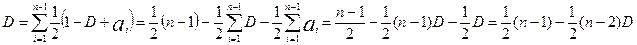
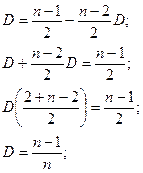
Из (6) найдем a_i

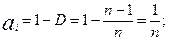
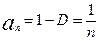
Следовательно, все коэффициенты a_i будут равны в уравнении прибыли.

Q_i=a_iQ_п

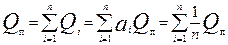
Чтобы определить цену С_i для каждого Q_i нужно Q_i подставить в уравнение (2).

ВЫВОД

В этой работе были использованы методы оптимизации стратегий продаж товара при известной кривой спроса. Нужно было решить 2 задачи:

1. Оптимизировать цену и размер партии товара, т.е. найти оптимальный размер партии и оптимальную цену, для продажи этой партии, чтобы получить максимальную прибыль.

После проведенных расчетов получено, что оптимальный размер партии равен 2,25, а оптимальная цена равна 7,5 у.е., при этом будет получена прибыль 9,6 у.е.

2. Определить оптимальную стратегию продажи заданной партии товара. Необходимо разделить партию на 2 части и определить цену для продажи каждой части таким образом, чтобы прибыль была максимальной .

После проведенных расчетов получено, что партию (Q_п=2,25) необходимо разделить пополам (по 1,125) и цена для первой партии равна 9,75 у.е., цена для второй партии равна 7,5 у.е. При этом мы получим прибыль 12,16 у.е.

Также было выведено аналитическое решение для расчета оптимальных размеров Q_i для общего случая деления партии товара на n частей.