Висловлення. Прості і складені висловлення
Кожне математичне речення характеризується змістом і логічною структурою. В математиці виділяють елементарні (прості) речення та складені. Наприклад: «Число 12 ділиться на 3» - просте речення ; «Число 42 - парне і ділиться на 3» - складене. Складені речення утворюються з елементарних та з логічних зв’язок . Логічні зв’язки - це слова : «і», «або», «не», «якщо, то», «тоді і тільки тоді» та інші.
Визначити логічну структуру математичного речення означає встановити :
з яких елементарних речень складене дане речення;
за допомогою яких логічних зв’язок воно утворене.
Речення позначаються великими буквами латинського алфавіту: А, В, С і т.д.
Логічна структура речень може мати такий вигляд: «А і В», «не А», «якщо А, то В», «А або В», «А тоді і тільки тоді, коли В».
Наприклад: речення – «Число 36 ділиться на 4 і 9» має логічну структуру – «А і В», де А – «Число 36 ділиться на 4», В – «Число 36 ділиться на 9», логічна зв’язка «і».
Висловлення - це речення, відносно якого має смисл питання, істинне воно, чи хибне.
Висловлення – це обов’язково стверджувальне речення . Наприклад: «3 + 2 = 5»; «7 < 8»; «Н2 S04 – кислота»; «Будь-який прямокутник є чотирикутником» і т.д. Висловлення, як і речення, позначаються великими літерами латинського алфавіту: А, В, С,....
Всі висловлення можна поділити на два класи: клас істинних і клас хибних висловлень. Отже, кожному висловленню можна поставити у відповідність одне з двох значень: І (істинне), або X (хибне), які називаються значеннями істинності.
Наприклад: висловлення «Число 125 ділиться на 5» – істинне, значення його істинності – І, а висловлення «5 < 3» - хибне, його значення істинності –X».
Висловлення поділяють на прості (елементарні) та складені. Значення істинності простих висловлень визначають за змістом, спираючись на відомі знання. Щоб встановити значення істинності складених висловлень, треба знати їх логічну структуру та смисл операцій над висловленнями.
3. Розглянемо операції, за допомогою яких із двох або більше простих висловлень можна будувати складені, та правила встановлення їх значень істинності.
Кон’юнкцією двох висловлень А і В називається складене висловлення  (читається А і В), яке істинне тоді і тільки тоді, коли істинні обидва висловлення А і В, що його утворюють, і хибне в усіх інших випадках.
(читається А і В), яке істинне тоді і тільки тоді, коли істинні обидва висловлення А і В, що його утворюють, і хибне в усіх інших випадках.
Кон’юнкцію двох висловлень дістають з двох простих, об’єднавши їх словом «і». Наприклад: «Середня лінія трикутника паралельна його основі і дорівнює її половині»; «24 - парне число і ділиться на 6».
Кон’юнкцію у математичній логіці називають логічним добутком. Значення істинності кон’юнкції висловлень можна подати за допомогою таблиці :
| А | В |  |
| І | І | І |
| І | X | X |
| X | І | X |
| X | X | X |
Наприклад, висловлення: «Число 15 - парне і ділиться на 3» має логічну структуру  , де А - просте висловлення: «Число 15 – парне»; В – «Число 15 ділиться на 3». Значення істинності висловлення
, де А - просте висловлення: «Число 15 – парне»; В – «Число 15 ділиться на 3». Значення істинності висловлення  = X, бо А – Х, В – І.
= X, бо А – Х, В – І.
Диз’юнкцією двох висловлень називається складене висловлення  (читається А або В), яке хибне тоді і тільки тоді, коли хибні обидва висловлення А і В, і істинне, якщо хоч би одне із них істинне.
(читається А або В), яке хибне тоді і тільки тоді, коли хибні обидва висловлення А і В, і істинне, якщо хоч би одне із них істинне.
Диз’юнкцію двох висловлень дістають, об’єднавши їх словом «або». Наприклад: «Рівняння х2-4=0 має корінь 2 або -2»; «Я поїду до Києва автобусом або поїздом».
Значення істинності операції диз’юнкції двох висловлень можна подати за допомогою таблиці:
| А | в |  |
| І | І | І |
| І | X | І |
| X | І | І |
| X | X | X |
Наприклад: висловлення «5 > 2» має логічну структуру  , що є диз’юнкцією двох висловлень; А: «5 більше 2», В: «5 дорівнює 2»; значення істинності його – І, бо А – X, В – І, а тому за означенням диз’юнкції
, що є диз’юнкцією двох висловлень; А: «5 більше 2», В: «5 дорівнює 2»; значення істинності його – І, бо А – X, В – І, а тому за означенням диз’юнкції  –І.
–І.
Заперечення висловлення А є таке висловлення 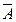 , яке істинне тоді і тільки тоді, коли А - хибне, і хибне, якщо А - істинне.
, яке істинне тоді і тільки тоді, коли А - хибне, і хибне, якщо А - істинне.
Наприклад, дано висловлення: А – «Десна - притока Дніпра», тоді висловлення 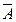 – «Десна не є притокою Дніпра» або «Неправильно, що Десна є притокою Дніпра» - є запереченням даного висловлення.
– «Десна не є притокою Дніпра» або «Неправильно, що Десна є притокою Дніпра» - є запереченням даного висловлення.
Таблиця істинності для заперечення висловлення А має вигляд:
| А | 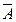 |
| І | X |
| X | І |
Наприклад:
А – «Число 3 є дільником числа 39» - істинне висловлення, тобто А = І, тоді його заперечення 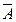 – «Число 3 не є дільником числа 39» за означенням – хибне висловлення :
– «Число 3 не є дільником числа 39» за означенням – хибне висловлення : 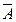 – X.
– X.
Імплікацією висловлень А і В називається висловлення «якщо А, то В», позначається так: А=> В, яке хибне тоді і тільки тоді, коли А - істинне, а В - хибне.
Наприклад, висловлення: «Якщо два кути вертикальні, то вони рівні»; «Якщо 25 < 42. то 42 > 25» є імплікаціями. Вони мають логічну структуру «А => В». Знак " =>" - це знак відношення слідування.
У шкільному курсі математики доводиться дуже часто мати справу з імплікаціями. Так, наприклад, кожна теорема є імплікацією висловлень. В імплікації: «А=> В», висловлення А називається умовою або посилкою, а висловлення В - висновком або наслідком. Таким чином, імплікація буде хибним висловленням лише тоді, коли з правильної посилки дістанемо неправильний висновок.
Таблиця істинності для імплікації має такий вигляд :
| А | В | А=> В |
| І | І | І |
| І | X | X |
| X | І | І |
| X | X | І |
Запис А => В читають по-різному: «з А слідує В»; «В слідує з А»; «якщо А, то В», «є А, отже, є і В».Наприклад, висловлення «Якщо число а ділиться на 9, то воно ділиться на 3» можна прочитати і так: «3 того, що число а ділиться на 9, слідує, що воно ділиться і на 3» або «Число а ділиться на 3 слідує з того, що воно ділиться на 9», «Число а ділиться на 9, отже, воно ділиться і на 3».
Якщо з висловлення А слідує висловлення В, то кажуть, що В - необхідна умова для А, А- достатня умова для В.
А => В
В - необхідна умова для А
А - достатня умова для В
Якщо з висловлення А слідує висловлення В, а із висловлення В слідує висловлення А, то кажуть, що висловлення А і В рівносильні.
Висловлення «А рівносильне В» записують за допомогою знаку "<=>". Запис «А <=> В» читають так: «А рівносильне В», «А тоді і тільки тоді, коли В». Якщо висловлення А і В рівносильні, то кажуть, що А необхідна і достатня умова для В і навпаки. Таку операцію називають еквіваленцією.
Еквіваленцієюдвох висловлень А і В називається таке висловлення А<=>В, яке істинне тоді і тільки тоді, коли обидва висловлення А і В мають однакові значення істинності.
| А | В |  |
| І | І | І |
| І | Х | Х |
| Х | І | Х |
| Х | Х | І |
Наприклад: висловлення – «Число х ділиться на 3 тоді і тільки тоді, коли сума цифр цього числа ділиться на 3» - є еквіваленцією. Воно має логічну структуру А <=> В, де А - це висловлення : «Число х ділиться на 3», а В - це висловлення: «Сума цифр числа х ділиться на 3». Істинність цього твердження доводиться.
4. Предикати (висловлювальні форми)
В математиці часто розглядають речення, які містять одну або декілька змінних. Наприклад: х > 3; х2 + 5х + 6 = 0; х + у = 7. Відносно цих речень не має смислу питання: істинні вони чи хибні, бо при одних значеннях змінної вони перетворюються в істинні висловлення, а при інших у хибні. Речення такого виду називаються предикатами або висловлювальними формами. Слово «предикат» у перекладі з латинської мови означає «присудок». Позначимо дані речення - h(х), f(х). Це висловлювальні форми від однієї змінної, або одномісна висловлювальна форма. Предикат «х = у» - є двомісним предикатом : р (х; у).
Висловлювальною формою або предикатом називається речення, яке містить одну або декілька змінних і яке перетворюється у висловлення при підстановці замість змінних конкретних значень.
Прикладами предикатів в шкільному курсі математики є: рівняння з однією або декількома змінними, нерівності зі змінними, системи рівнянь або нерівностей тощо. Найпоширеніші з предикатів в математиці мають свої позначення. Наприклад: «х дорівнює у» позначається «х = у»; «х менше або дорівнює у» позначається «х ≤ у»; «х паралельно у» позначається «х || у».
Відносно висловлювальної форми виникає питання: при яких значеннях змінної ця форма перетворюється в істинне або хибне висловлення. Якщо це рівняння, нерівність, система рівнянь чи нерівностей, то для відповіді на це питання їх треба розв’язати, тобто знайти їх множини розв’язків.
Наприклад: знайти множину істинності предикатів: 2х = 10; х = 25;  >3.
>3.
Для відповіді на це запитання необхідно розв’язати дані рівняння, нерівність та вказати при яких значеннях х вони перетворюються у правильні числові рівності або правильну числову нерівність, тобто у істинні висловлення. Множинами істинності даних предикатів є множини їх розв’язків.
Квантори
Часто у висловленнях використовуються слова «всі», «деякі», «будь-які», «існує», «хоч би один», «кожен», «знайдеться» тощо.
Наприклад: «Всі числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – одноцифрові», «Деякі з одноцифрових чисел діляться на 3», «Існують рівносторонні трикутники» тощо. Відносно цих речень можна сказати, що вони істинні або хибні, а тому ці речення є висловленнями. Якщо ж з даних речень забрати слова «всі», «деякі», «існують», то вони перетворюються у предикати.
Слова «всі», «деякі» тощо називаються кванторами. Слово «квантор» латинського походження і означає «скільки», тобто квантор показує, про скільки об’єктів (про всі чи про деякі) іде мова у даному реченні.
Розрізняють квантори загальності та існування. Квантори загальності позначають знаком  (перевернута перша буква англійського слова All - всі), а квантори існування знаком
(перевернута перша буква англійського слова All - всі), а квантори існування знаком 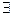 (перевернута перша буква англійського слова Exists – існує).
(перевернута перша буква англійського слова Exists – існує).
Квантори загальності (  ) ) | Квантори існування ( 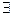 ) ) |
| всі | існує |
| кожен | хоч би один |
| будь-який | деякі |
| довільний | знайдеться |
Форму висловлення з предикатом мають багато математичних речень, наприклад, «всі ромби є паралелограмами»; «деякі непарні числа діляться на 5»; «сума кутів будь-якого трикутника дорівнює 180°».
Правила встановлення значень істинності висловлень, що містять квантори,подані у таблиці:
| Висловлення з квантором |  А А | 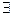 А А |
| І | шляхом доведення | навести приклад |
| X | навести контрприклад | шляхом доведення |
Для побудови заперечення висловлень, що містять квантори існує два способи:
1. Перед даним висловленням ставляться слова «неправильно, що».
2. Квантор загальності (існування) замінюється квантором існування (загальності), а речення, яке стоїть після квантора, замінюється його запереченням.
Наприклад: побудувати заперечення двома способами висловлення «Будь-яке натуральне число ділиться на 5».
1 спосіб: «Неправильно, що будь-яке натуральне число ділиться на 5».
2 спосіб: «Існує натуральне число, яке не ділиться на 5».
Структура і види теорем
План
1. Структура теореми.
2. Види теорем.
3. Найпростіші схеми правильних міркувань.
Структура теореми
Теорема – це твердження, істинність якого доводять. Теорема містить умову і висновок.
А  В
В
А – умова, В – висновок.
Можна сказати, що теорема – це висловлення про те, що з властивості А слідує властивість В. Істинність цього висловлення встановлюється шляхом доведення.
Не кожна ознака А, необхідна для В, є і достатньою, так само як і не кожна достатня ознака є необхідною. Наприклад, щоб число ділилось на 3, достатньо, щоб воно ділилось на 9, але це не є необхідною умовою, наприклад 6 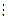 3, але 6 не
3, але 6 не 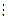 9 (знак «
9 (знак « 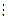 » – знак подільності). Щоб число ділилось на 6, необхідно, щоб воно ділилось на 2, але цього не достатньо, необхідно також щоб воно ділилось і на 3. Отже, щоб число ділилось на 6, необхідно і достатньо, щоб воно ділилось і на 2, і на 3. За допомогою складеного висловлення символічно це можна записати так:
» – знак подільності). Щоб число ділилось на 6, необхідно, щоб воно ділилось на 2, але цього не достатньо, необхідно також щоб воно ділилось і на 3. Отже, щоб число ділилось на 6, необхідно і достатньо, щоб воно ділилось і на 2, і на 3. За допомогою складеного висловлення символічно це можна записати так:
а 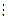 6
6 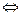 (а
(а 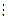 2)
2) 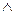 (а
(а 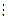 3).
3).
Інакше а ділиться на 6 тоді і тільки тоді, коли а 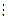 2 і а
2 і а 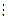 3.
3.
Якщо і умова теореми, і її висновок є простими висловленнями, то теорема називається простою.
Якщо умова або висновок теореми, або і те, і друге – складені висловлення, то теорему називають складеною. Попередня теорема, що виражає ознаку подільності на 6, є складеною. Її можна записати у вигляді А 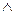 В
В  С. Тут умова є кон’юнкцією двох висловлень А і В, а висновок – висловлення С.
С. Тут умова є кон’юнкцією двох висловлень А і В, а висновок – висловлення С.
Приклад аналогічної структури теореми: «Якщо дві прямі площини перпендикулярні до третьої прямої, то вони паралельні між собою»
або (а  с)
с) 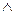 ( в
( в  с)
с)  а ║в.
а ║в.
Приклад теореми, в якій і умова, і висновок є кон’юнкціями: «В паралелограмі протилежні сторони попарно рівні». Інакше: «Якщо чотирикутник – паралелограм (тобто протилежні сторони попарно паралельні), то його протилежні сторони попарно рівні».
Тобто (а║с) 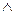 (b║d)
(b║d)  ( a = c)
( a = c) 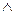 (b = d)
(b = d)
До сталих компонентів структури теореми належать такі:
1 2 3
|
|
|




5 4

|
|

|


 6
6
Структурна сталість компонентів 1, 2, 3 зумовлена тим, що питання про істинність теореми всіма розв’язується однозначно, набір же логічних операцій (4), послідовності їх використання можуть бути різними. Тут великі можливості для творчої розумової діяльності, для формування інтелектуальних умінь в процесі доведення теорем.
Види теорем
Розрізняють пряму, обернену, протилежну і обернену до протилежної теореми.
1. А  В – пряма теорема,
В – пряма теорема,
2. В  А – обернена теорема,
А – обернена теорема,
3. 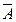

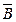 - протилежна теорема,
- протилежна теорема,
4. 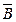

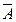 - обернена до протилежної теорема.
- обернена до протилежної теорема.
Пряма і обернена до протилежної теореми є рівносильними.
Приклад: «Якщо кути вертикальні, то вони рівні» – пряма теорема.
А: «кути вертикальні», В: «кути рівні».
А  В – пряма теорема.
В – пряма теорема.
Обернена: В  А: «Якщо кути рівні, то вони вертикальні».
А: «Якщо кути рівні, то вони вертикальні».
Протилежна: 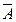

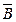 : «Якщо кути не вертикальні, то вони не рівні».
: «Якщо кути не вертикальні, то вони не рівні».
Обернена до протилежної: 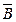

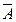 : «Якщо кути не рівні, то вони не вертикальні».
: «Якщо кути не рівні, то вони не вертикальні».
Існує зв'язок між названими видами теорем. Встановлено, що теореми А  В і
В і 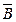

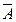 рівносильні, тобто А
рівносильні, тобто А  В
В 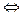
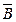

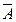 . Отриману рівносильність називають законом контрапозиції.
. Отриману рівносильність називають законом контрапозиції.

