Элементамимножества: запись обозначает принадлежность

элемента а множеству А , запись 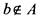обозначает, что элемент b не

принадлежит А . Множество 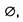не содержащее ни одного элемента, называется пустым Равенство множеств А и В (запись А = В) означает, что А и В состоят из одних и тех же элементов. Если каждый элемент множества А принадлежит множеству В , то говорят, что А есть подмножествоВ , или А входит в В (запись 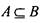). Среди

подмножеств любого множества В - пустое множество 0 и само В . Множества А и В равны, когда выполнены оба вхождения: 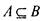и

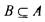
Множество считается заданным, если каким-либо образом указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. В таком случае задание множества выглядит

так {X :< условие Р >} и читается- "множество элементов X , для

которых выполнено условие 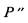(здесь X - обозначение элемента). В ряде случаев целесообразно рассматривать несколько множеств

в качестве подмножеств универсальногомножества U. Множество элементов U , которые не принадлежат некоторому множеству называется дополнениеммножества А (обозначение ).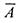

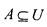
Если А , В - два множества, то с помощью теоретико-множественных операций могут быть получены другие множества. ОбъединениеС (обозначение 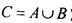) - это множество, состоящее

из всех элементов, принадлежащих хотя бы одному из множеств А , В . ПересечениеС (обозначение 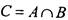) - это множество элементов,

принадлежащих обоим множествам А и В. РазностьС множеств А и В (обозначение 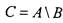) - это множество элементов множества

А , не принадлежащих множеству В .

Стандартные обозначения для некоторых наиболее употребительных числовыхмножеств:

N - множество натуральных чисел (иногда его начинают с 1, иногда с 0; обычно это оговаривается);

Z - множество целых чисел (положительные, отрицательные и 0); Q - множество рациональных чисел, т.е. чисел, равных частному от деления двух целых чисел;

R - множество действительных чисел. Очевидное соотношение: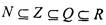

Множества, обозначаемые теми же прописными латинскими буквами [ с подстрочным знаком "+" или "-", например Z₊или /?_ суть

j подмножества множеств Z и R , состоящие из чисел соответствующего знака.

Подмножества упомянутых числовых множеств, состоящие из чисел,

находящихся между двумя числами а , b , называются промежутками:

• интервал(открытый промежуток)обозначается

_; (а,Ь);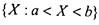

Iотрезок(замкнутый промежуток) 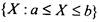обозначается

[ [а,Ь];

t

: а и b называются концами промежутка: отрезок содержит оба своих

\ конца, интервал не содержит ни одного. Полуинтервалы(а, Ь]и [а, Ь), содержащие один конец промежутка, определяются аналогично. Бесконечные промежутки 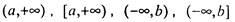суть

множества чисел, удовлетворяющих соответственно соотношениям

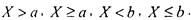
Высказываниемназывается любое повествовательное предложение, относительно которого имеет смысл утверждать либо, что оно истинно,либо, что оно ложно(установить истинность того или иного высказывания бывает не просто, - иногда для этого нужно решить серьезную задачу). Предложение, содержащее переменную, при различных значениях которой оно становится истинным или ложным, называется неопределенным высказыванием.

Из простых высказываний p,q строятся сложныес помощью следующих основных логических операций:

конъюнкцияесть высказывание " р и q " (обозначения 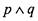или

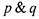), которое истинно тогда и только тогда, когда истинны оба составляющих высказывания p,q\

дизъюнкция- высказывание "р или q" (обозначение ),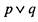

истинное тогда и только тогда, когда истинно хотя бы одно из высказываний p,q\

импликация- высказывание "если р , то q ", или "из р следует <7 " (обозначение 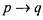), которое ложно тогда и только тогда, когда р

истинно, a q - ложно;

эквивалентность- высказывание " р эквивалентно q" (обозначение 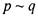), истинное в том и только в том случае, если р и q

оба истинны, либо оба ложны.

Отрицанием высказывания р называется высказывание "не Р",

или "неверно, что р " (обозначение 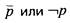), истинное тогда и только

тогда, когда р ложно.

Обозначая истинность буквой И, а ложность - буквой Л, можно задать упомянутые операции таблицами.

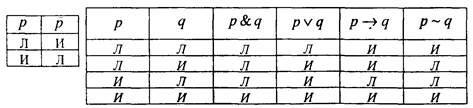
Неопределенному высказыванию Р(Х), содержащему переменную X, можно сопоставить высказывания ."для всех X Р(Х) истинно", обозначаемое 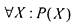, _и "существует X такое, что Р(Х) истинно",

обозначаемое 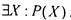такие операции называются кванторами:

квантором общности V и квантором существования 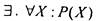- высказывание истинное, если для всякого (каждого, любого) X выполнено Р(Х) и ложное, если, напротив, существует 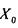, для которого 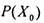ложно. 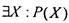- высказывание истинное, если хотя

бы для одного 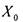высказывание 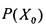истинно, и ложное, если,

напротив, такого 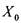нет, т.е. для всех X Р(Х) ложно. ГЛАВА 1. ФУНКЦИОНАЛЬНЫЕ СООТВЕТСТВИЯ И ОТНОШЕНИЯ