Відстань, діаметр, радіус і центр графу
Нехай G - зв’язний, неорієнтований граф. Оскільки дві довільні вершини „a” і „b” – зв’язані, то в загальному випадку існує декілька простих ланцюгів Si(a, b), які з’єднують „a” і „b”. В цій множині ланцюгів має існувати ланцюг, який має найменшу довжину. Ця найменша довжина і називається відстанню між „a” і „b”: d(a, b). Будемо вважати за визначенням, що d(a, a) = 0.
Введена відстань задовольняє всі аксіоми метрики:
1) d(a, b) ³ 0;
2) d(a, b) = 0 тоді і тільки тоді, коли a = b;
3) d(a, b) = d(b, a);
4) d(a, b) + d(b, c) ³ d(a, c).
Для скінченного графу можна ввести поняття діаметру.
Визначення. Діаметр графу G(V):
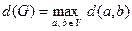 .
.
Виберемо деяку вершину c Î V і позначимо через
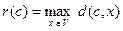 ,
,
віддаль від с до найбільш віддаленої вершини графу.
Назвемо c0 центром графу G, якщо
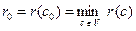 .
.
Зауважимо, що центр графу не єдиний.
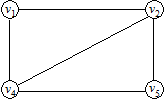
Рис.6
Наприклад, для графу, зображеного на рис. 6, радіус r0 = 1; центр графу c0 = v2 або c0 = v4.
Алгоритм Дейкстри
Розглянемо наступну задачу: заданий скінченний орієнтований граф G, кожному ребру якого приписана його числова характеристика („довжина”). Необхідно знайти найкоротший шлях від заданої вершини (позначимо її через s) до всіх решта вершин графу.
Для розв’язання цієї задачі найбільшого розповсюдження набув алгоритм Декстри, згідно з яким всі вершини графу G(V) необхідно впорядкувати по зростанню їх відстані від вершини s:
d(s, u0) £ d(s, u1) £ … £ d(s, un) і V = { u0, u1, …, un}.
Ця послідовність будується інтеративно. Перша вершина в ній відома:
u0 = s; d(s, u0) = 0.
Нехай відомі перші (l + 1) вершини цієї послідовності:
{u0 = s, u1, …, ul},
які ми будемо надалі називати фіксованими. Це означає, що вершина u1 ближча від s, ніж всі решта (тобто нефіксовані) вершини.
Для кожної нефіксованої вершини у графу модифікуємо її відстань від s: якщо існує e(ui, v) і d(s, ui) + d(ui, v) £ d(s, v) , то d(s, v) = d(s, ui) + d(ui, v) і передостанньою вершиною в найкоротшому (на даний час) шляху, який з’єднує s з v, буде вершина ui. Після цього серед всіх нефіксованих вершин знаходимо ту, відстань до якої від s є найменшою. Ця вершина і буде наступною в послідовності (тобто ui + 1).
Алгоритм Дейкстри.
Масиви, що використовуються:
VID: VID(i) – найкоротша на даний момент відстань від s до i -ї вершини графу;
FIX: FIX(i) = 1, якщо i-та вершина графу є фіксованою;
PRED: PRED(i) містить передостанню вершину в найкоротшому з усіх відомих на даний момент шляхів від s до і-ї вершини графу.
1) Початкові установки.
Для початкової вершини: VID(s) = 0, FIX(s) = 0, PRED(s) = s.
Для всіх інших вершин графу: VID(v) = ¥, FIX(v) = 0, PRED(v) = v.
Біжуча вершина: u = s, i = 1.
2) Цикл по тих вершинах графу G, для яких FIX(v) = 0
якщо існує e = (u, v) і VID(u) + d(u, v) £ VID(v)
то VID(v) = VID(u) + d(u, v), PRED(v) = u.
3) Серед вершин графу G, для яких FIX(v) = 0, знаходимо ту вершину v0, для якої
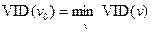 .
.
4) FIX(v0) = 1, u = v0.
5) i = i + 1.
якщо i £ n,
то йти на 2).
6) Кінець.
В результаті масив VID містить найкоротші відстані від s до всіх вершин графу; по масиву PRED можна отримати найкоротший шлях від s до довільної вершини графу.
Приклад.
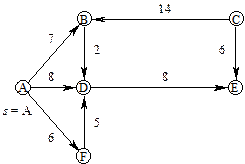
Рис.7
Робота алгоритму проілюстрована в табл. 5, в якій кожний рядок відповідає одному циклу роботи алгоритму. Фіксовані вершини підкреслені, а біля вершини „u” на кожному кроці стоїть зірочка.
Таблиця 5
| i | VID | PRED | ||||||||||
| A | B | C | D | E | F | A | B | C | D | E | F | |
| 0* | ∞ | ∞ | ∞ | ∞ | ∞ | A | B | C | D | E | F | |
| ∞ | ∞ | 6* | A | A | C | A | E | A | ||||
| 7* | ∞ | ∞ | A | A | C | A | E | A | ||||
| ∞ | 8* | ∞ | A | A | C | A | E | A | ||||
| ∞ | 16* | A | A | C | A | D | A | |||||
| ∞ | A | A | C | A | D | A |
Найкоротший шлях від A, наприклад, до E будується, використовуючи масив PRED, таким чином: E D A.
Задача про ланцюги
Теорія графів почалася з розв’язування задачі про кенігсберзькі мости (Ейлер, XVIII ст.). Розташування мостів в м. Кенігсберг наведено на рис.8.

Рис. 8.
В місті є 7 мостів {a, b, c, d, e, f, g}, які його розбивають на чотири частини {A, B, C, D}. Необхідно обійти всі мости міста, проходячи по кожному рівно один раз, і повернутись у початкову точку.
Граф для цієї задачі наведений на рис.9.

Рис.9.
Загальна постановка задачі є наступною (Ейлер): в яких випадках у скінченному неорієнтованому графі можна знайти такий цикл, у якому кожне ребро графу зустрічалось би рівно один раз. Якщо такий цикл існує, то він називається ейлеревим циклом, а сам граф називається ейлеревим.
Твердження. Скінченний граф G(V) є ейлеровим тоді і тільки тоді, коли:
1) G(V) - зв’язний граф;
2) локальні степені всіх його вершин парні.
Алгоритм побудови ейлеревого циклу:
1) вибираємо довільну вершину a Î V;
2) будуємо довільний ланцюг P з початком у вершині „a”. Оскільки локальні степені всіх вершин графу є парні, то ланцюг може завершитись тільки в „a” (тобто він є циклом);
3) якщо P(a, a) містить не всі ребра графу G(V), то будуємо граф G1 = G ‑ P(a, a), в якому всі вершини мають теж парний локальний степінь. Оскільки граф G(V) є зв’язним, то серед вершин P(a, a) має знайтись вершина „b”, яка зв’язана ребром хоча б з однією вершиною графу G(V) (інакше граф G був би незв’язним);
4) будуємо з ребер графу G1 ланцюг P’, що починається у вершині „b” і може закінчуватись тільки у „b”; з ланцюгів P і P’ будуємо новий цикл:
P1(a, a) = P(a, b) È P’(b, b) È P(b, a);
5) якщо P1(a, a) не містить всіх ребер графу G(V), то, за аналогією з кроком 3) будуємо граф G2 = G – P1(a, a) і т.д.
З огляду на скінченність графу, цей процес зупинитися, коли всі ребра графу G(V) будуть вичерпані.
Узагальнюючи задачу Ейлера можна шукати найменшу кількість ланцюгів (не циклів!) P1, які не перетинаються по ребрах і покривають увесь зв’язний граф G(V).
Твердження. Нехай G(V) - скінченний зв’язний граф з k вершинами непарного локального степеня. Тоді мінімальна кількість ланцюгів, які не перетинаються по ребрах і покривають граф G, дорівнює k / 2.
Алгоритм побудови ланцюгів Pi.
1) з’єднуємо довільно чином пари вершин з непарним локальним степенем (для цього необхідно k / 2 ребер). При цьому утворюється граф G1, всі вершини якого мають парний степінь;
2) граф G1 є ейлеровим і в ньому існує ейлерів цикл S;
3) після відкидання з циклу S доданих на кроці 1) k / 2 ребер, отримуємо k / 2 ланцюгів, які покривають весь граф G.
Приклад
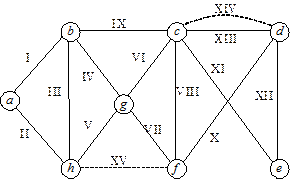
Рис. 10.
Степені вершин графу:
| Вершина | a | b | c | d | e | f | g | h |
| Степінь |
Таким чином, k = 4. З’єднаємо ребрами вершини (c, d) та (f, h) (на рис.10 ці ребра позначені штриховими лініями).
Поетапно побудуємо для утвореного графу цикл Ейлера:
а) P1 = (І, ІІІ, ІІ);
б) P2 = (І, ІХ, VI, IV, III, II);
в) P3 = (І, IX, XIII, XII, XI, VI, IV, III, II);
г) P4 = (I, IX, XIV, X, VIII, XIII, XII, XI, VI, IV, III, II);
д) P5 = (I, IX, XIV, X, VIII, XIII, XII, XI, VI, VII, XV, V, IV, III, II).
Віднімаючи додані раніше ребра XIV і XV, отримаємо три ланцюги:
1) (І, Х);
2) (Х, VIII, XIII, XII, XI, VI, VII);
3) (V, IV, III, II).
Зауважимо, що перший і третій ланцюги мають спільний кінець – вершину „а”. „Склеюючи” ці ланцюги, отримаємо остаточно:
1) (V, IV, III, II, I, IX);
2) (X, VIII, XIII, XII, XI, VI, VII).
Для орієнтованих графів має місце
Твердження. Нехай G(V) - орієнтований зв’язний граф. Граф G містить ейлерів цикл тоді і тільки тоді, коли у кожну вершину v входять стільки ж ребер, скільки і виходить:
r(v) = r*(v).
Якщо в неорієнтованому графі кожне неорієнтоване ребро замінити двома орієнтованими і протилежно направленими, то мають місце умови попереднього твердження і тому правильне таке
Твердження. У скінченному зв’язному неорієнтованому графі завжди можна побудувати орієнтований цикл, який проходить через кожне ребро по одному разу в кожному з двох напрямків.
Гамільтонові цикли
Визначення. Гамільтонів цикл – це цикл, який проходить по кожній вершині графа і рівно один раз.
До знаходження гамільтонового циклу приводить, наприклад, задача комівояжера: деякий район містить пеану кількість міст, які повинен обійти комівояжер. Відомі відстані між всіма містами. Необхідно знайти найкоротший шлях, який проходить через всі міста і повертається в початковий пункт.
Незважаючи на подібність у формулюванні для ейлерових і гамільтонових циклів, відповідні теорії мають мало спільного. Критерій існування ейлеревих циклів був встановлений достатньо просто; для гамільтонових циклів ніякого загального правила невідомо. Більше того, для конкретних графів іноді тяжко встановити, чи існує взагалі такий цикл. Тому обмежимось одним критерієм.
Твердження. (Дірак). Якщо в графі G(V) з n вершинами для довільної вершини v Î V : r(v) ³ n / 2, то в графі існує гамільтонів цикл.
На закінчення зауважимо, що є різні задачі пошуку маршрутів у графі:
- з’ясування чи граф є ейлеревим та знаходження відповідного ейлеревого циклу
- знаходження найменшої кількості ланцюгів, які не мають спільних ребер та покривають увесь граф
- з’ясування чи граф є гамільтоновим
- знаходження маршрут, що зв’язує дві довільні задані вершини
- знайти найкоротший шлях з однієї заданої вершини в іншу задану вершину (зокрема для зважених графів)
Деякі класи графів
Дерева
Дерева - це особливий і дуже важливий клас графів. Особлива роль дерев визначається як широким їхнім застосуванням у різних галузях науки і практики, так і тим особливим положенням, яке дерева займають у самій теорії графів. Останнє випливає з граничної простоти будови дерев. Часто при розв’язуванні різних задач теорії графів їхнє дослідження починають з дерев. Зокрема, порівняно нескладною є проблема перевірки ізоморфності дерев.
Твердження 1. В дереві дві довільні вершини зв’язані єдиним ланцюгом (інакше був би цикл).
Твердження 2.Довільний ланцюг у дереві є простим.
Визначення. У довільному графі G вершина v називається кінцевою, якщо r(v) = 1, тобто існує одне ребро, інцидентне вершині v, і це ребро називається кінцевим.
Твердження 3. У дереві є хоча б дві кінцеві вершини.
Розглянемо дерево G і виберемо довільну вершину v0. Кожному ребру e = (a, b) зіставимо той кінець, який більш віддалений від v0 (оскільки в дереві всі ланцюги є простими, то від довільної вершини до v0 веде лише один ланцюг).
Твердження 4.Для дерева виконується рівність vV – vE = 1 (vV - кількість вершин, vE - кількість ребер).
Твердження 5. У дереві кожне ребро суттєве (його вилучення веде до порушення зв’язаності графа).
Визначення. В довільному скінченному зв’язаному графі G циклічний ранг:
g(G) = vE ‑ vV + 1.
Твердження. Для довільного скінченного зв’язаного графа G циклічний ранг
g(G) ³ 0
і дорівнює кількості ребер, які необхідно вилучити з G для того, щоб отримати дерево (скелет графа).
Для дерев g(G) = 0.
Дерева використовують для розв’язання такої задачі: необхідно з’єднати „n” міст залізничною колією таким чином, щоб не будувати зайвих ліній. При цьому вважається відомим вартість будівництва колії між двома довільними містами. Таким чином, необхідно побудувати зв’язний граф G, який містить всі задані вершини і для якого повна вартість 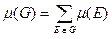 була б найменшою. Очевидно, що граф G - дерево.
була б найменшою. Очевидно, що граф G - дерево.
Алгоритм розв’язання.
Вибираємо ребро ei з найменшою вартістю. Отримаємо граф A1 = {e1}. На кожному наступному кроці до Ai ‑ 1 додаємо ребро, яке має найменшу вартість серед тих, що залишились, і таке, що граф Ai = Ai ‑ 1 È {ei} не має циклів. Останній граф An ‑ 1 = G і є шуканим.
Двочасткові графи
Граф G =(V,E ) називається двочастковим, якщо існує розбиття {V1,V2} множини вершин V на дві підмножини (частки) таке, що для довільного ребра (v,w)ÎE виконується або v ÎV1 i w ÎV2, або v ÎV2 i w ÎV1.
Двочастковий граф G =(V,E ) називається повним двочастковим графом, якщо для будь-якої пари вершин його часток v ÎV1 i w ÎV2 маємо (v,w)ÎE. Якщо |V1|=m i |V2|=n, то повний двочастковий граф G позначається Km,n.
Теорема (теорема Кеніга). Граф є двочастковим тоді і тільки тоді, коли всі його цикли мають парну довжину.
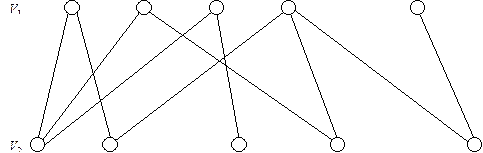
Визначення. Нехай G(V1, V2) - дводольний граф. Пароз’єднання – це підмножина ребер графу G:{(xi, yj), …}, де xi Î V1 а yj Î V2, причому жодні два ребра не мають спільних вершин.
Визначення. Максимальне пароз’єднання (П) – це пароз’єднання дводольного графу G, яке має найбільшу кількість ребер.
Розглянемо таку задачу: знайти максимальне пароз’єднання, яке містить всі вершини множини V1.
Твердження (теорема Холла). Максимальне пароз’єднання П дводольного графу покриває всі вершини множин V1 тоді і тільки тоді, якщо для довільної множини U1 Í V1 кількість елементів у множині U2 Í V2, яка містить всі вершини, з’єднані ребром хоча б однією вершиною з U1, не менша від кількості вершин множини U1.
Алгоритм побудови максимального пароз’єднання П.
Будемо вважати, що умови теореми Холла виконані. Задамося довільним пароз’єднанням П0. Якщо воно не охоплює всіх вершин множини V1, то існує x0 : x0Î V1 і x0Ï П0.
Побудуємо
W0 = {x0};
W1 = {y | (x0, y) Î G};
W2 = {x | (x, y) Î П0, y Î W1, x Ï W0};
W3 = {y | (x, y) Î G, x Î W2, y Ï W1};
W4 = {x | (x, y) Î П0, y Î W3, x Ï W0 È W2};
W5 = {y | (x, y) Î G, x Î W4, y Ï W1 È W3};
. . .
Зауважимо, що, згідно з побудовою, в множинах W1 і W2, W3 і W4, W5 і W6 і т.д. попарно однакова кількість елементів. Крім того, послідовність вершин Wi не може закінчитись на множині з парним індексом W2k, оскільки для множини
U1 = W0 È W2È … È W2k Í V1
кількість вершин у відповідній множині
U2 = W1 È W3È … È W2k - 1 Í V2
(U2 містить всі вершини графу, які з’єднані ребром хоча б з однією з вершин множини U1) на одиницю більше, що суперечить умові теореми Холла. Тому існує вершина y*:
y* Î W2k - 1 і y* Ï П0.
Тоді існує шлях S, який починається з x0, проходить через вершини множин W1 і закінчується в y* і містить непарну (2k ‑ 1) кількість ребер:
S = {e1, e2, …, e2k - 1},
причому всі парні ребра e2k Î П0.
Нове пароз’єднання П1 будуємо наступним чином:
П1 = П0 \ {e2 È e4 È…È e2k - 2} È {e1 È e2 È…È e2k - 1}.
Пароз’єднання П1 містить на одне ребро і на одну вершину з множини V1 більше ніж П0. Якщо П1 охоплює всі вершини множини V1, то беремо деяку вершину x0 : x0Î V1 і x0Î П1 і т.д.
Приклад
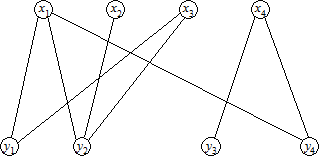
П0 = {(x1, y1), (x3, y2)}.
1) W0 = (x2); W1 = (y2); W2 = (x3); W3 = (y1); W4 = (x1); W5 = (y4).
e1 = (x2, y2); e2 = (x3, y2); e3 = (x3, y1); e4 = (x1, y1); e5 = (x1, y4).
П1 = {(x2, y2), (x3, y1), (x1, y4)}.
2) W0 = (x4); W1 = (y3, y4).
e1 = (x4, y3).
П = П2 = {(x1, y4), (x2, y2), (x3, y1), (x4, y3)}.
5. Плоскі та планарні графи
У багатьох випадках не має особливого значення, як зобразити граф у вигляді рисунка на площині (діаграми), оскільки ізоморфні графи подібні за своєю структурою і містять ту саму інформацію. Однак існують ситуації, коли необхідно, щоб зображення графа на площині задовольняло певні умови. Наприклад, якщо граф є моделлю деякої електронної схеми або транспортної мережі, де вершинами є окремі елементи схеми або станції, а ребрами, відповідно, - електричні провідники і шляхи, то бажано так розташувати ці ребра на площині, щоб уникнути перетинів.
Таким чином виникає поняття плоского графа.
Граф називається плоским, якщо його діаграму можна зобразити на площині так, що лінії, які відповідають ребрам графа, не перетинаються (тобто мають спільні точки тільки у вершинах графа). Таке зображення називається плоскою картою графа.
Граф називають планарним, якщо він ізоморфний деякому плоскому графу.
Наприклад, граф, зображений на рис., планарний, оскільки він ізоморфний графу, зображеному поруч. Простий цикл, дерево і ліс - це також планарні графи.
Про планарні графи кажуть, що вони укладаються на площині або мають плоске укладання.
 | |||
 | |||
а) б)
Рис.
При дослідженні плоских графів особливе місце займають графи K5 i K3,3, зображені на рис.
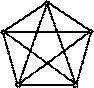 | |||
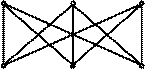 | |||
K5 K3,3
Рис.
Граф K3,3 виникає із задачі про три хати і три криниці.
Теорема. Графи K5 i K3,3 не є планарними.
Значення графів K5 i K3,3 полягає в тому, що вони є "єдиними" суттєво непланарними графами. Всі інші непланарні графи містять у собі підграфи "подібні" до K5 або K3,3. Характер цієї подібності розкривається за допомогою таких понять.
Елементарним стягуванням графа G =(V,E ) називається вилучення в графі G деякого ребра (vi,vj)ÎE і злиття вершин vi i vj в одну вершину v, причому v інцидентна всім тим відмінним від (vi,vj) ребрам графа G, які були інцидентні або vi , або vj.
Кажуть, що граф G стягується до графа G ¢, якщо G ¢ можна отримати з G за допомогою послідовності елементарних стягувань.
Приклад . На рис. зображено графи G i G ¢, при цьому G стягується до G ¢.
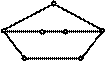 | 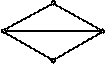 | ||
G G ¢
Рис.
Наведемо без доведення важливу теорему теорії графів.
Теорема (теорема Куратовського). Граф G є планарним тоді і тільки тоді, коли він не містить підграфів, що стягуються до K5 або K3,3.
Розфарбування графів
Нехай G =(V,E ) довільний граф, а Nk={1,2,...,k }.
Будь-яке відображення f :V ® Nk, яке ставить у відповідність кожній вершині v ÎV деяке натуральне число f (v) ÎNk, називається розфарбуваннямграфа G. Число f (v)називається кольором або номером фарби вершини v.
Розфарбування f графа G називається правильним, якщо для будь-яких його суміжних вершин v і w виконується f (v) ¹ f (w).
Мінімальне число k, для якого існує правильне розфарбування графа G, називається хроматичним числом графа G і позначаєтьсяc(G ).
Мінімальним правильним розфарбуваннямграфа G називається правильне розфарбування для k=c(G ).
Для певних типів графів визначити хроматичні числа нескладно. Наприклад, 1-хроматичними є порожні графи G =(V,Æ) і тільки вони. Хроматичне число повного графа Kn дорівнює n, а хроматичне число довільного двочасткового графа - 2. 2-хроматичні графи часто називають біхроматичними.
Очевидними є такі твердження.
Лема 3.6. Якщо кожна зв’язна компонента графа G потребує для свого правильного розфарбування не більше k фарб, то c(G )£k.
Лема 3.7. Граф є біхроматичний тоді і тільки тоді, коли він двочастковий.
Зокрема, всі дерева і прості цикли парної довжини C2k є біхроматичні. У той же час, c(C2k+1)=3.
Використовуючи теорему 3.12 (Кеніга), останню лему можна переформулювати у такому вигляді.
Лема 3.8. Граф є біхроматичний тоді і тільки тоді, коли він не має циклів непарної довжини.
Проблема визначення, чи є заданий граф k-хроматичним для певного k, та проблема знаходження мінімального правильного розфарбування для заданого графа належать до класу задач, для яких на сьогодні не існують (і є всі підстави вважати, що не існують взагалі) ефективні точні алгоритми їх розв’язку. Тому важливими є результати, які дозволяють оцінити значення хроматичного числа c(G ), виходячи з певних характеристик та властивостей графа G.
Теорема 3.16. Позначимо через D(G ) найбільший зі степенів вершин графа G, тоді c(G ) £ D(G )+1.
Доведення проведемо індукцією за кількістю n вершин графа G. Для тривіального графа (n=1) і графів з двома вершинами нерівність виконується.
Нехай твердження теореми виконується для всіх графів з кількістю вершин t (t ³ 2). Розглянемо довільний граф G з t +1 вершиною. Вилучимо з G деяку вершину v, дістанемо граф G ¢, всі степені вершин якого не перевищують D(G ). Отже, за припущенням індукції, для правильного розфарбування G ¢ потрібно не більше ніж D(G )+1 фарба. Правильне розфарбування для G дістанемо з правильного розфарбування графа G ¢, якщо пофарбуємо вершину v у колір, відмінний від кольорів усіх суміжних із v вершин. Оскільки таких вершин не більше, ніж D(G ), то для правильного розфарбування графа G достатньо D(G )+1 фарба.
Наслідок 3.16.1. Для правильного розфарбування довільного кубічного графа достатньо чотири фарби.
Так склалося історично, що окреме місце в теорії графів займають дослідження з розфарбування планарних графів. Пов’язано це зі славетною проблемою або гіпотезою чотирьох фарб.
Грані плоскої карти назвемо суміжними, якщо їхні межі мають принаймні одне спільне ребро.
Гіпотеза чотирьох фарб виникла у зв’язку з розфарбуванням друкованих географічних карт (звідси й термін "плоска карта") і формулювалась так:
“Грані довільної плоскої карти можна розфарбувати не більше ніж чотирма фарбами так, що будь-які суміжні грані матимуть різні кольори”.
Згодом з’явилось інше, рівносильне, формулювання гіпотези чотирьох фарб.
Для правильного розфарбування вершин довільного планарного графа потрібно не більше чотирьох фарб.
Ця гіпотеза виникла в середині ХIХ століття. Більше ста років професійні та непрофесійні дослідники намагалися довести або спростувати цю гіпотезу. В результаті багаторічних досліджень виявилось, що для вирішення проблеми чотирьох фарб необхідно перевірити її справедливість для скінченного числа графів певного виду. Кількість варіантів, які потрібно було перебрати, була настільки великою, що тільки за допомогою потужної ЕОМ, яка неперервно працювала протягом більше двох місяців, у 1976 році справедливість гіпотези чотирьох фарб була підтверджена. Однак такий "фізичний" експериментальний спосіб доведення не зовсім влаштовує багатьох професійних математиків, і вони продовжують пошуки аналітичного доведення гіпотези.
На завершення зауважимо, що існують планарні графи, хроматичне число яких дорівнює 4. Найпростішим таким графом є K4. Отже, гіпотезу чотирьох фарб не можна "вдосконалити", перетворивши у "гіпотезу трьох фарб".
Список літератури
1. Дискретна математика: Підручник / Ю.М.Бардачов, Н.А.Соколова, В.Є.Ходаков; за ред. В.Є.Ходакова. – К.: Вища школа, 2002. – 287с.
2. Основи дискретної математики: Підручник / Ю.В.Капітонова, С.Л.Кривий, О.А.Летичевський, Г.М.Луцький, М.К. Печурін. – К.: Наукова думка, 2002. – 568с.
3. Луцький Г.М., Кривий С.Л., Печурін М.К. Основи дискретної математики. – К.: ВІПОЛ, 1995. – 252с.
4. Бородін О.I., Потьомкін Л.В., Сліпенко А.К. Основні поняття сучасної алгебри. - К.: Вища школа, 1993. -112 с.
