Определение дисперсии воспроизводимости
Определение среднего арифметического значения параллельных опытов на основном уровне:
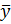 =
= 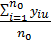
где 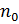 - число параллельных опытов на основном уровне
- число параллельных опытов на основном уровне
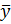 =
= 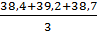 =
= 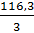 = 38,76667
= 38,76667
Определение дисперсии воспроизводимости:
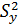 =
= 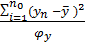
где, 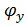 – число степеней свободы:
– число степеней свободы: 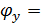
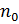 – 1 = 3 – 1 = 2
– 1 = 3 – 1 = 2
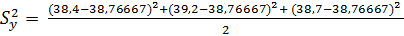 = 0,163333
= 0,163333
3.2. Вычисление коэффициентов уравнения регрессии[3]
y = b0 + b1x1 + b2x2 + b3x3 + b12x1x2 + b13x1x3 + b23x2x3 + b123x1x2x3
Для удобства расчета коэффициентов уравнения составляем расширенную матрицу планирования.
Результаты сводим в таблицу 5.
Таблица 5. Расширенная матрица планирования
| № | x0 | x1 | x2 | x3 | x12 | x13 | x23 | x123 | y |
| + | + | + | + | + | + | + | + | 76,2 | |
| + | - | + | + | - | - | + | - | 60,0 | |
| + | + | - | + | - | + | - | - | 35,5 | |
| + | - | - | + | + | - | - | + | 26,7 | |
| + | + | + | - | + | - | - | - | 41,0 | |
| + | - | + | - | - | + | - | + | 35,1 | |
| + | + | - | - | - | - | + | + | 11,8 | |
| + | - | - | - | + | + | + | - | 9,5 |
b0 = 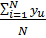
где, N – число опытов
b0 = 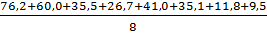 =
= 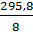 = 36,975
= 36,975
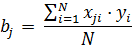
где, j,i – номер фактора;
N – число опытов.
b1 = 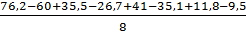 =
= 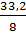 = 4,15
= 4,15
b2 = 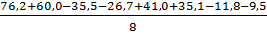 =
= 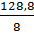 = 16,1
= 16,1
b3 = 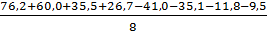 =
= 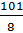 = 12,625
= 12,625
b12 = 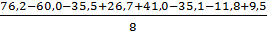 =
=  = 1,375
= 1,375
b13 = 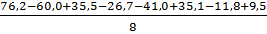 =
= 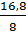 = 2,1
= 2,1
b23 = 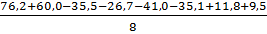 =
= 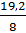 = 2,4
= 2,4
b123 = 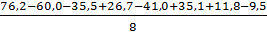 =
= 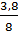 = 0,475
= 0,475
Уравнение имеет следующий вид
y= 36,975+ 4,15x1 +16,1x2 + 12,625x3 +1,375x12 + 2,1x13 + 2,4x23 + 0,475x123
Проверка статистической значимости
Определение дисперсии коэффициентов уравнения
S{b}2 = 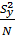 =
= 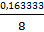 = 0,020417
= 0,020417
S{b} = S{b}2 = 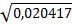 = 0,142887
= 0,142887
Определение доверительного интервала
Проверку значимости коэффициентов проводим при помощи доверительных интервалов:
∆b = S{b}· tT(φ;α)
где, tT – табличное значение критерия Стьюдента [1];
α – уровень значимости, α=0,05
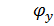 – число степеней свободы:
– число степеней свободы: 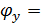
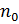 – 1 = 3 – 1 = 2
– 1 = 3 – 1 = 2
tT(φ;α) = tT(2;0,05) = 4,303
∆b = 0,142887· 4,303 = 0,614843
Если |bj| > ∆b, то коэффициент значим
|b1| > ∆b
|b2| > ∆b
|b3| > ∆b
|b12| > ∆b
|b13| >∆b
|b23| > ∆b
|b123| < ∆b
Уравнение со значимыми коэффициентами:
y= 36,975+ 4,15x1 +16,1x2 + 12,625x3 +1,375x12 + 2,1x13 + 2,4x23
Незначимый коэффициент: 0,475x123 исключают.
Так как матрица ортогональна, то оставшиеся коэффициенты не пересчитываются.
Проверка адекватности модели
Определение дисперсии адекватности
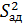 =
= 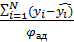
где, 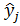 - значение параметра оптимизации, рассчитанные по модели для условий i-го опыта
- значение параметра оптимизации, рассчитанные по модели для условий i-го опыта
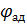 – число степеней свободы
– число степеней свободы
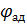 = N – (k+1) = 8 – (6 + 1) = 1
= N – (k+1) = 8 – (6 + 1) = 1
где, k – число значимых коэффициентов, без коэффициента b0
y= 36,975+ 4,15x1 +16,1x2 + 12,625x3 +1,375x12 + 2,1x13 + 2,4x23
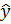 1 = 36,975+ 4,15 +16,1 + 12,625 +1,375 + 2,1 + 2,4= 75,725
1 = 36,975+ 4,15 +16,1 + 12,625 +1,375 + 2,1 + 2,4= 75,725
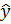 2 = 36,975-4,15 +16,1 + 12,625 -1,375 - 2,1 + 2,4=60,475
2 = 36,975-4,15 +16,1 + 12,625 -1,375 - 2,1 + 2,4=60,475
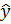 3 = 36,975+ 4,15 -16,1 + 12,625 -1,375 + 2,1 - 2,4=35,975
3 = 36,975+ 4,15 -16,1 + 12,625 -1,375 + 2,1 - 2,4=35,975
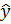 4 =36,975-4,15 -16,1 + 12,625 +1,375- 2,1 - 2,4=26,225
4 =36,975-4,15 -16,1 + 12,625 +1,375- 2,1 - 2,4=26,225
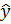 5 = 36,975+ 4,15 +16,1 - 12,625 +1,375 - 2,1 -2,4=41,475
5 = 36,975+ 4,15 +16,1 - 12,625 +1,375 - 2,1 -2,4=41,475
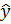 6 = 36,975-4,15 +16,1 - 12,625 -1,375 + 2,1 -2,4=34,625
6 = 36,975-4,15 +16,1 - 12,625 -1,375 + 2,1 -2,4=34,625
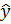 7 = 36,975+ 4,15 -16,1 - 12,625 -1,375 - 2,1 + 2,4=11,325
7 = 36,975+ 4,15 -16,1 - 12,625 -1,375 - 2,1 + 2,4=11,325
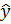 8 = 36,975- 4,15 -16,1 - 12,625 +1,375 + 2,1+2,4=9,975
8 = 36,975- 4,15 -16,1 - 12,625 +1,375 + 2,1+2,4=9,975
Результаты расчета приведены в Таблице 5.
Таблица 5. Результаты расчета параметра оптимизации
| № | y | 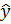 | |(y - 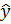 | | | 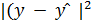 | |
| 76,2 | 75,725 | 0,475 | 0,225625 | ||
| 60,0 | 60,475 | 0,475 | 0,225625 | ||
| 35,5 | 35,975 | 0,475 | 0,225625 | ||
| 26,7 | 26,225 | 0,475 | 0,225625 | ||
| 41,0 | 41,475 | 0,475 | 0,225625 | ||
| 35,1 | 34,625 | 0,475 | 0,225625 | ||
| 11,8 | 11,325 | 0,475 | 0,225625 | ||
| 9,5 | 9,975 | 0,475 | 0,225625 | ||
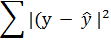 | 1,805 | ||||
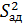 =
= 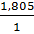 = 1,805
= 1,805
Проверка гипотезы адекватности
Для проверки гипотезы адекватности воспользуемся критерием Фишера [1]. Определяется расчетное значение критерия Фишера и сравнивается с табличным:
Fp = 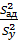 =
= 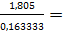 11,05104
11,05104
где, Fp - расчетное значение критерия Фишера;
Fт - табличное значение критерия Фишера Fт (α, φу, φад)
α= 0,05;
φу = 2;
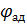 = 1
= 1
Fт (α, φу, φад) = 199,5
Если Fp < Fт (11,05104< 199,5) то гипотеза об адекватности модели принимается, модель адекватна.
ЗАКЛЮЧЕНИЕ
Данное уравнение:
y= 36,975+ 4,15x1 +16,1x2 + 12,625x3 +1,375x12 + 2,1x13 + 2,4x23
пригодно для описания влияния факторов алюминотермического способа восстановления Ме из фторида в выбранных интервалах варьирования.
Наибольшее влияние на данный процесс оказал фактор: х2 – температура процесса восстановления (tпр),°С;
В меньшей степени влияют факторы: х3 – продолжительность процесса восстановления, мин и x1 – количество восстановителя,%.
СПИСОК ЛИТЕРАТУРЫ
1. Ходарев О.Н. Планирование и организация эксперимента: учебн. пособие / Юж. -Рос.гос.техн.ун-т (НПИ) - Новочеркасск: ЮРГТУ (НПИ), 2010- 146 с.
2. Горбатенко Н.И., Ланкин М.В., Шайхутдинов Д.В. Планирование эксперимента: учебн. пособие / Юж. -Рос.гос.техн.ун-т (НПИ). - Новочеркасск: Оникс+, 2007. - 120 с.
3. Рогов В.А., Поздняк Г.Г. Методика и практика технических экспериментов: Учебн. пособие для студ. высш. учебн. заведений - М.: Издательский центр "Академия", 2005. - 288 с.
