Кездейсоқ процестер және олардың негізгі сипаттамалары.

Статикалық сипаттамасы барлық қималарында бірдей болатын кездейсоқ процестерді, кездейсоқ стационарлы процесс деп аталады.

Математикалық күтімі m және процестің дисперсиясы σ² уақытқа байланысты болмай, ал корреляция функциясы тек 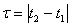айырмашылығына байланысты болса, яғни 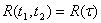, онда бұл процесс кең мағынада стационарлы болады. Анықтама бойынша кездейсоқ стационарлы процесстің корреляция функциясы жұп болады 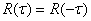. Сонымен қатар кез келген функцияның абсолютті мәні τ өспейді, τ=0 болғанда

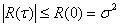. (9.1)

Егер кездейсоқ стационарлы процесстің мезеттік функциясын табу кезінде статистикалық ансамбль бойынша орташалауда уақыт бойынша орташалаумен ауыстырып, оны эргодикалық деп атаймыз. Орташалау операциясы тек х(t) арқылы жүзеге асса, онда Т ұзақтылығы теориялық тұрғыдан үлкен болуы мүмкін. Уақыт бойынша орташалауды бұрыштық жақшамен белгілеп, таңдалған нақтылықтың тұрақты құраушысына тең, кездейсоқ эргодикалық процесстің математикалық күтімін жазамыз:

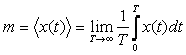, (9.2)

Осындай процесстің дисперсиясы

. (9.3)

<x²> мәні нақтылаудың орта қуатын, ал m² мәні тұрақты құраушының қуатын білдірсе, дисперсия эргодикалық процесстің флуктуациялық құраушысының қуаты болып табылады.

Сәйкесінше, корреляция функциясын былай табады.

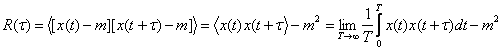. (9.4)

Егер шарты орындалса, кездейсоқ процесс эргодикалық болады.

. (9.5)

Корреляция интервалы 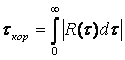. (9.6)

9.6 сәйкес корреляция интервалы анықтамасын шамамен тікбұрышты әдіс деп аталатын: корреляция интервалы биіктігі 1 болатын тікбұрыштың табанына тең, ал ауданы τ≥0-ден болғандағы қисықтың ауданына|R(τ)| тең.

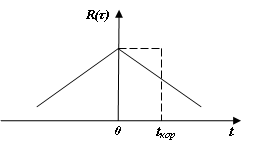
9.1 Сурет - Корреляция интервалын тікбұрышты шама әдісімен анықтау

Кездейсоқ процесстерді сипаттау үшін корреляция функциясымен бірге спектрлік сипаттамасы, ал жеке жағдайда қуаттың спектрлі жазықтығы G(f) кең қолданылады. B(τ) және G(f) арасында Фурье түрлендіруі қолданылады. Кездейсоқ стационарлы процесстер үшін бұл қатынасты А.Я.Ханчин және Винер негізген.

СЖ дисперсиясын (орташа қуаты) жиілік бойынша интегралдау жолымен табуға болады.

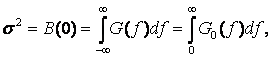
мұнда, G₀(f) оң жиіліктерде анықталған ҚСЖ. Тікбұрышты шамалас әдісімен (немесе басқа өлшемдері) СЖ корреляция интервалын (B(τ) енінің) ғана емес, сонымен қатар (G₀(f) енінің) F_э енін табуға болады. Бұл шамалардың туындысы τ_кор F_э.~К шартын қанағаттандырады, К-мұнда тұрақты ҚСЖ сипатталатын, барлық жиілікте (9.2 а суретті қара) бірдей кездейсоқ процесс ақ шу деп аталатын (оптикадағы ақ түске сәйкес).

Егер спектрі G₀(f)=N₀ жоғарысында жиілігімен шектелесе (9.2 б суретті қара), процесс квази ақ шуыл деп аталады. Оның дисперсиясы σ² = B(0) = N₀F_B. Квази ақ шудың КФ табайық:

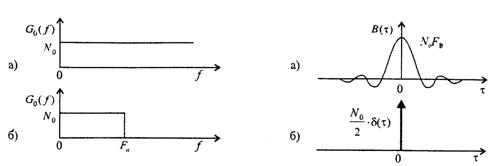9.2 Сурет – ақ (а) және квази ақ (б) шудың орташа қуатының спектрлі жазықтығы	9.3 Сурет- квази ақ (а) және ақ шудың корреляция функциясы

Алынған КФ 9.3 а суретінде бейнеленген. Қысқарған мәнінде, нөл арқылы өтетінін көреміз:

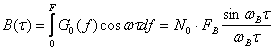. (9.7)

Бұл, (бүтін сан) интервалымен бөлінген қиылу процессінің өзара корреляцияланбағанын көрсетеді. Егер шекаралық жиілігін шексіз үлкейтсек, сәйкес емес екі қиылысу корреляцияланбаған кездейсоқ шудан, абсолютті кездейсоқ процесске өтеміз (ақ шуға); Ақ шудың КФ функциясымен 9.2 б суретте өрнектеледі.

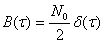. (9.8)

Егер фнукцияның анықтамасын пайдалансақ, 9.8-дің қорытындысы 9.7-ге қатысты.

Бұндай процессті тудыратын орташа қуат шексіз үлкен болғандықтан, ақ шу нақты процесстің математикалық тұрғыдан іске асуы болып табылады.

Ақ шулы түрдегі бөгеуілдің мысалы ретінде тәжірибеге дейінгі жиілікті қамтитын біркелкі спектрлі жазықтықты регистрдің жылулық шуын алуға болады.