Теорема Гаусса для электростатического поля в вакууме

Поток вектора напряженностичерез элементарную площадку 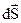равен: 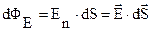(рисунок 3)

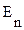— проекция вектора 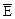на нормаль 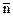к площадке dS.

Рисунок 3. Поток вектора напряженности через элементарную площадку.

Для произвольной замкнутой поверхности S поток вектора 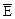через эту поверхность: 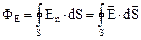— интеграл по замкнутой поверхности S.

Поток вектора напряженности — алгебраическая величина, т.е. зависит не только от конфигурации потока Е, но и от выбора направления нормали 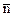. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т.е. нормаль, направленная наружу области, охваченной поверхностью.

Поток вектора напряженности сквозь сферическую поверхность радиуса r (с площадью поверхности 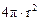), охватывающую точечный заряд q, находящейся в ее центре:

.

Теорема Гаусса:

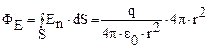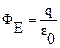
Формула справедлива для замкнутой поверхности любой формы.

Если замкнутая поверхность не охватывает заряда, то поток вектора напряженности через нее равен 0.

Если замкнутая поверхность охватывает n зарядов, то в соответствии с принципом суперпозиции, когда каждое из слагаемых суммы равно 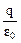, и поток вектора напряженности через замкнутую поверхность:

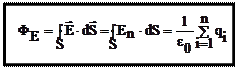
— теорема Гаусса в