Обработка экспериментальных данных. 1. Вычисляются значения коэффициента давления по формуле
1. Вычисляются значения коэффициента давления по формуле
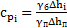 ,
,
где 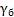 – удельный вес жидкости в манометре (для подкрашенной воды
– удельный вес жидкости в манометре (для подкрашенной воды 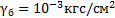 ) [1].
) [1].
2. На миллиметровке выстраиваются координатные диаграммы 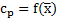 и
и 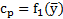 . Для этого, используя данные табл. 14.1, наносятся экспериментальные точки (
. Для этого, используя данные табл. 14.1, наносятся экспериментальные точки ( 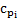 ,
, 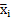 ) и (
) и ( 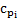 ,
, 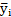 ). Эти точки соединяют плавными кривыми. Надписями «
). Эти точки соединяют плавными кривыми. Надписями « 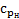 » и «
» и « 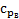 » отмечаются кривые, дающие распределение давления на верхней и нижней поверхности крыла (рис.14.2); на другой диаграмме отмечаются надписями «
» отмечаются кривые, дающие распределение давления на верхней и нижней поверхности крыла (рис.14.2); на другой диаграмме отмечаются надписями « 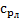 » и «
» и « 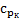 » кривые распределения давления на лобовой и кормовой частях профиля (рис.14.3).
» кривые распределения давления на лобовой и кормовой частях профиля (рис.14.3).
3. Далее следует вычислить значение безразмерного коэффициента 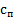 , используя формулу Симпсона для численного интегрирования [1]:
, используя формулу Симпсона для численного интегрирования [1]:
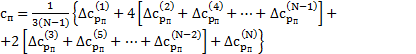 .
.
Для использования этой формулы весь интервал 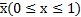 разбивают на
разбивают на 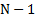 равных частей, причем
равных частей, причем 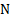 – обязательно число нечетное. Любое
– обязательно число нечетное. Любое 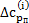 есть значение
есть значение 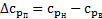 в точке с координатой
в точке с координатой 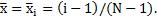 При практическом расчете значения
При практическом расчете значения 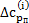 снимаются с графика замером расстояния между кривыми
снимаются с графика замером расстояния между кривыми 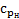 и
и 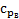 при соответствующей координате
при соответствующей координате  с учетом знака алгебраической величины
с учетом знака алгебраической величины 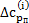 . Значения
. Значения 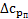 в крайних точках, как видно из рис. 14.2, всегда равны нулю, т. е.
в крайних точках, как видно из рис. 14.2, всегда равны нулю, т. е. 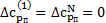 .
.
Как показывает расчетная практика, число 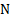 вполне достаточно выбирать равным порядка
вполне достаточно выбирать равным порядка 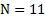 .
.
4. Аналогично при вычислении второго безразмерного коэффициента [1]:
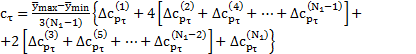 ,
,
где 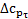 – значение
– значение 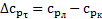 в точке с координатой
в точке с координатой
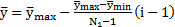 .
.
Это значение может быть определено непосредственным измерением расстояния между кривыми 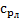 и
и 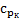 на рис. 14.3 при соответствующей координате
на рис. 14.3 при соответствующей координате  . И точно так же должен быть учтен знак величины
. И точно так же должен быть учтен знак величины 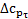 . Здесь, как и при вычислении значения
. Здесь, как и при вычислении значения 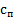 , число
, число 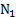 – обязательно нечетное, a
– обязательно нечетное, a 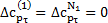 .
.
5. Вычисленные значения 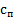 и
и 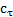 позволяют найти аэродинамические коэффициенты
позволяют найти аэродинамические коэффициенты 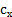 и
и 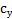 согласно формулам [1]:
согласно формулам [1]:
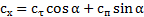 ,
,
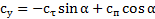 .
.
6. Для вычисления коэффициента тангажного момента 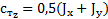 необходимо вычислить интегралы:
необходимо вычислить интегралы:
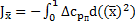 ,
,
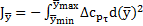 .
.
Для этой цели можно предложить ту же методику численного интегрирования, что и при вычислении коэффициентов 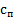 и
и 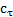 . Поэтому прежде всего должны быть графически построены зависимости
. Поэтому прежде всего должны быть графически построены зависимости 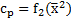 и
и 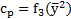 . Разбив интервал интегрирования
. Разбив интервал интегрирования 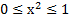 на четное число отрезков, можно с использованием формулы Симпсона вычислить интеграл
на четное число отрезков, можно с использованием формулы Симпсона вычислить интеграл 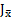 , а затем аналогично и
, а затем аналогично и 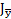 .
.
7. Положение центра давления можно найти по формуле
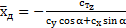 .
.
Форма отчета.
Таблица 14.1 – Регистрация и обработка опытных данных [1]
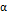 , град. , град. | 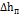 , см , см | отв.№ | |||||||||||||||
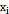 | |||||||||||||||||
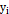 | |||||||||||||||||
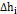 | |||||||||||||||||
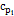 | |||||||||||||||||
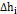 | |||||||||||||||||
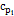 | |||||||||||||||||
 | |||||||||||||||||
 |
Точность измерений должна быть до десятых долей сантиметра.
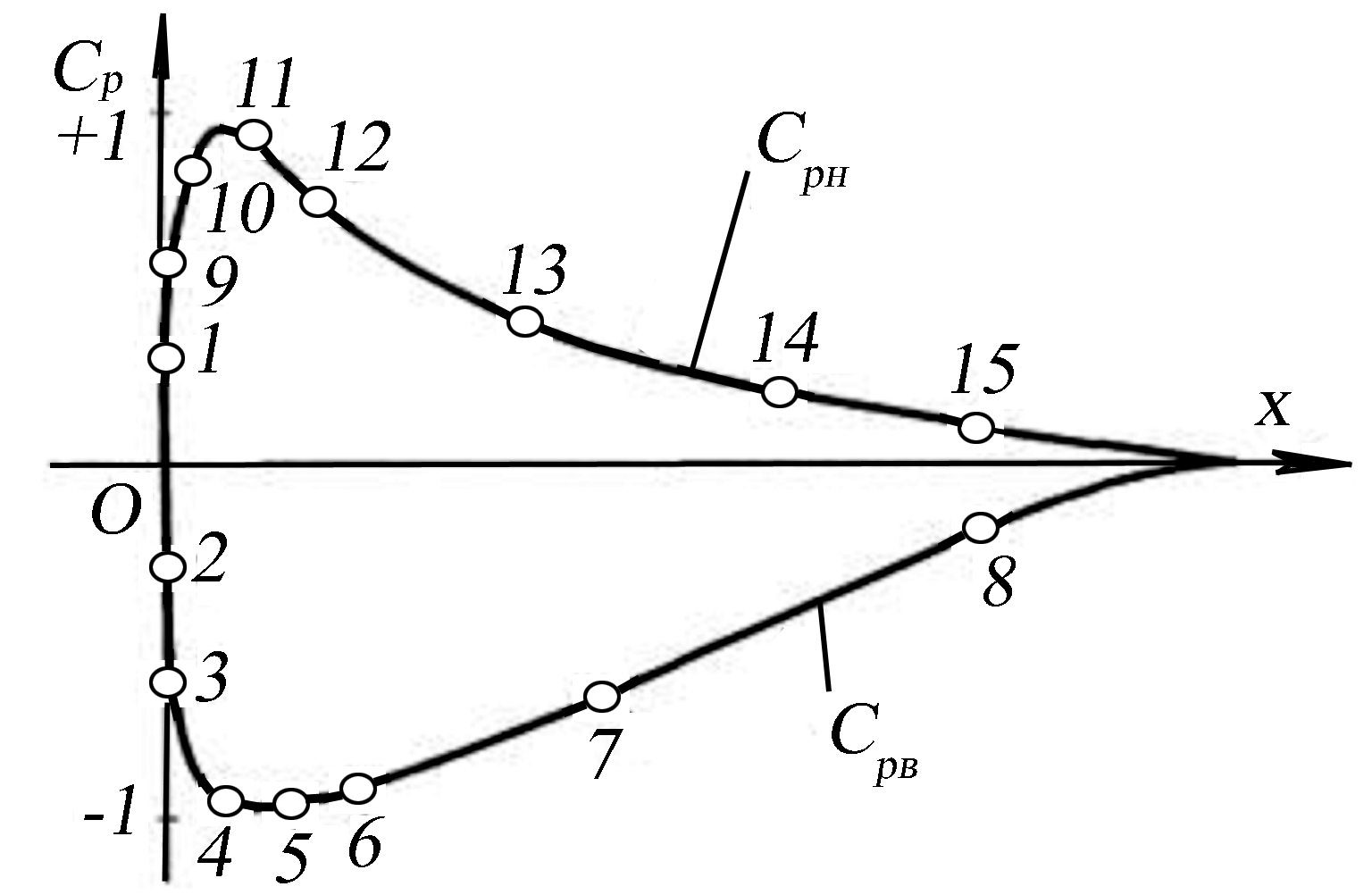
Рис. 14.2. Распределение давления на верхней и нижней частях профиля крыла [1]
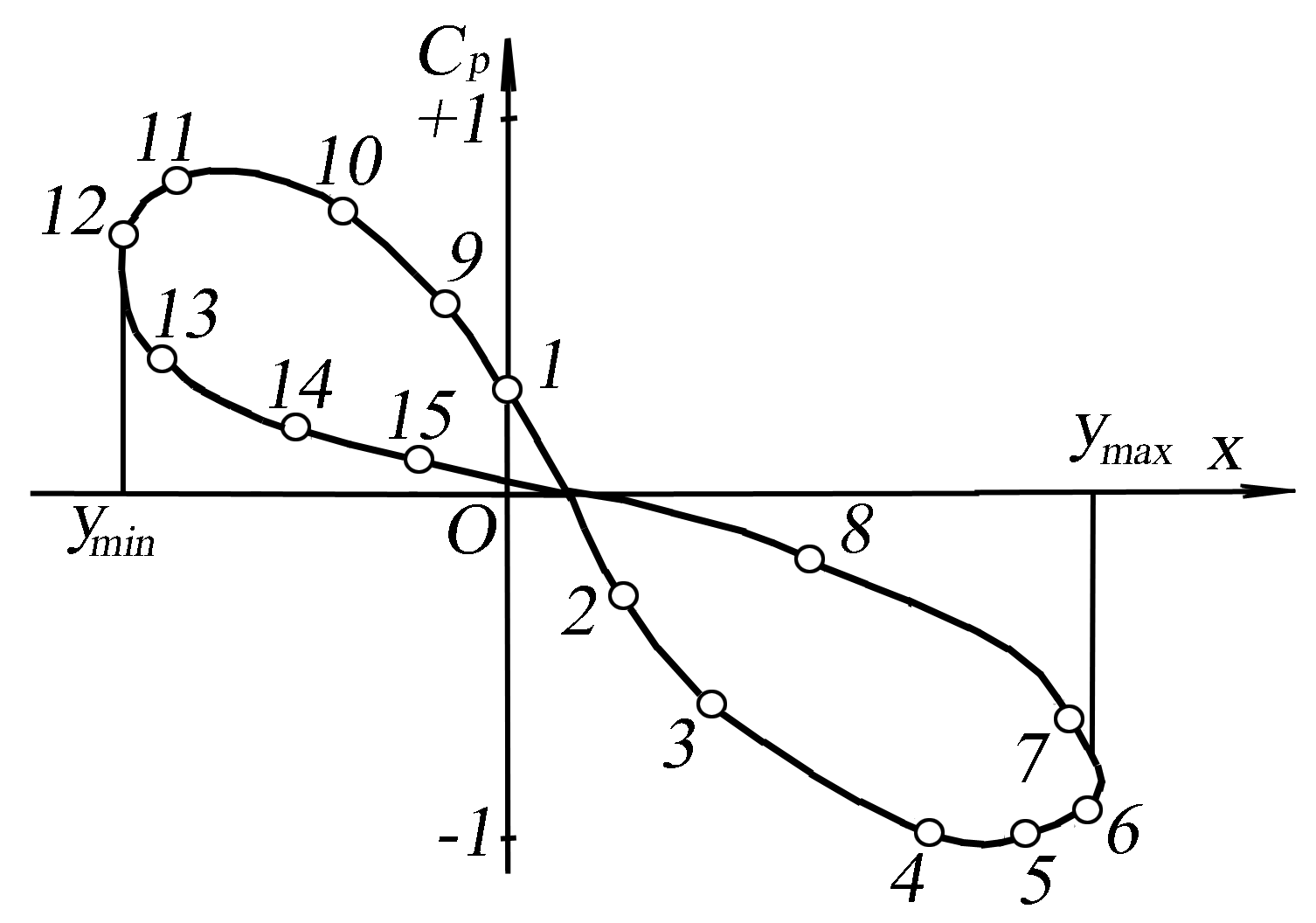
Рис. 14.3. Распределение давления
на лобовой и кормовой частях профиля крыла [1]
Кроме приведенной выше таблицы и графиков в отчете по лабораторной работе должен быть представлен следующий графический материал:
1) схема взаимного расположения осей и действующих на крыло сил (рис.14.4) [1];
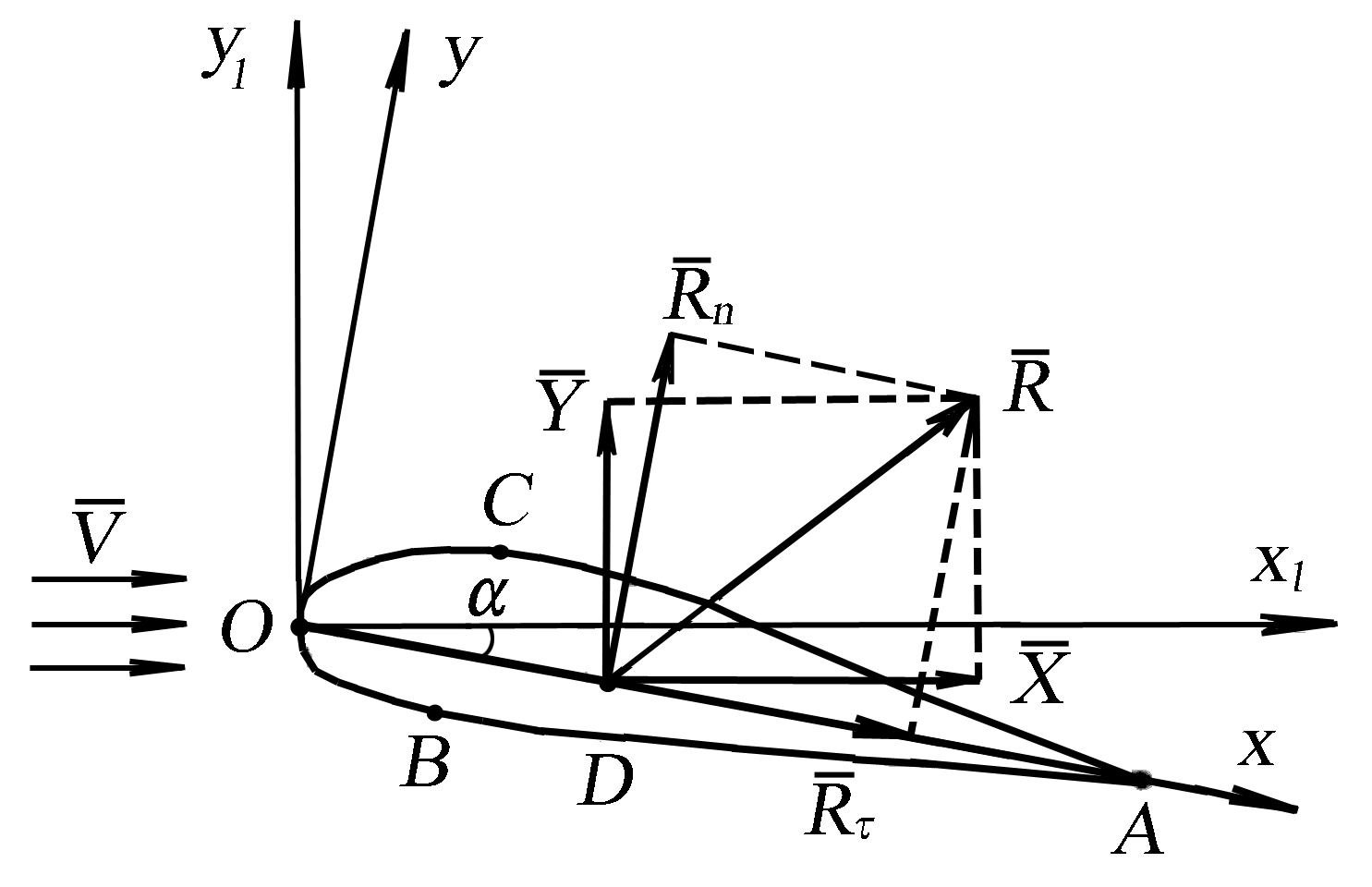
Рис. 14.4. Расположение центра давления крыла [1]
2) схема трубки Пито-Прандтля;
3) графики зависимостей 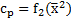 и
и 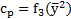 ;
;
4) векторная диаграмма распределения безразмерного избыточного давления 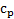 по поверхности крыла (рис.14.5) [1]. На этом чертеже крыловой профиль вычерчивается геометрически подобным и указывается масштаб отложенных значений
по поверхности крыла (рис.14.5) [1]. На этом чертеже крыловой профиль вычерчивается геометрически подобным и указывается масштаб отложенных значений 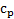 .
.
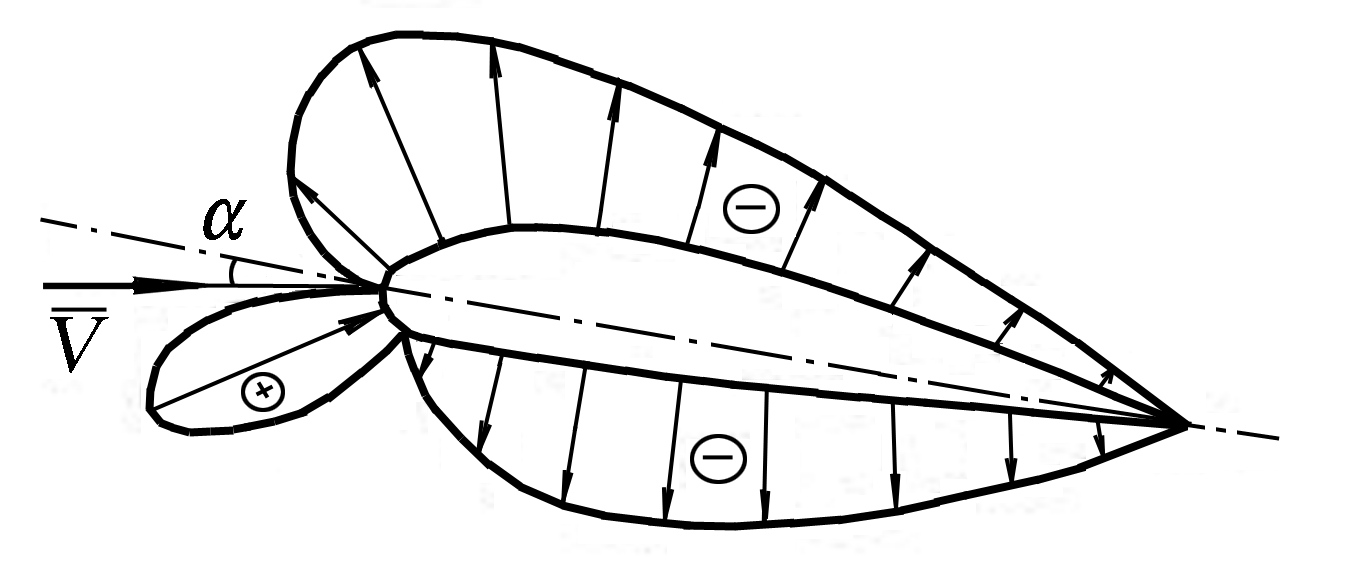
Рис.14.5. Векторная диаграмма распределения избыточного давления
по поверхности крыла [1]
7. Контрольные вопросы:
1. Объясните принцип измерения скорости в потоке газа при помощи трубки Пито-Прандтля.
2. Запишите формулу для определения скорости звука. Поясните ее физический смысл.
3. Поясните, какие силы действуют на профиль, обтекаемый потоком газа.
Лабораторная работа № 15
