Поиск максимального потока. 3 страница

ШагF.На этом шаге определяются кратчайшие пути из начальной вершины 0 во все вершины x≠0. Кратчайший путь из начальной вершины 0 в любую другую вершину xстроится следующим образом: вершиной, предшествующей xна искомом пути, является вершина y = R(x); вершиной, предшествующей yна искомом пути, является вершина z = R(y), и т.д., вплоть до начальной вершины 0. Искомый путь из 0 в xсостоит из тех же вершин в обратном порядке ■

При «ручной» реализации АД будет удобно промежуточные результаты записывать в таб-лицу, строки которой соответствуют итерациям, а столбцы (кроме двух левых) – вершинам. В самом левом столбце будем писать номер итерации, а 2-ой слева столбец выделим для записи очередной помечаемой вершины с и её постоянной метки P(с). Каждую клетку в остальных столбцах таблицы разделим на 3 части, в которые будем записывать текущее значение Z, новое значение временной метки Т и новую предыдущую вершину R, или писать старые значения, в зависимости от результата сравнения в пункте 2) шага i-A. После того, как вершина получила постоянную метку, в её клетки ничего не записываем. Числа l(c,x) – длины рёбер – берутся непосредственно из рисунка.

Пример 1. Рассмотрим применение АД для графа, показанного на рис.1. Длины рёбер на-писаны на рисунке прямо около них. Составим вышеупомянутую таблицу.

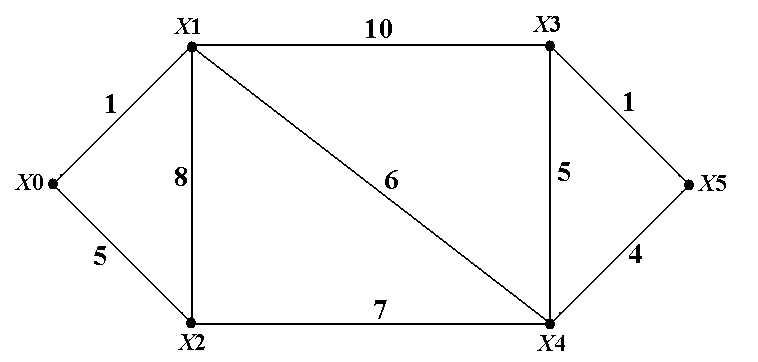
Рис.1. Граф с длинами рёбер

Таблица 1

Итера- ция

Последняя помеченная

Вершина 0

Вершина 1

Вершина 2

Вершина 3

Вершина 4

Вершина 5

№

с

P

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

Дадим пояснения к заполнению таблицы 1. На 0-ой итерации (инициализации) в соответс-твии с АД начальной вершине 0 присваиваем постоянную метку 0 (оба числа заносятся в 0-ую строку в столбце «Последняя помеченная»). Остальные вершины получают временную метку ∞, которая и заносится в 0-ую строку под буквами T. В остальные позиции 0-ой строки в соот-ветствии с АД ничего не заносится.

На 1-ой итерации обрабатываются только столбцы, соответствующие вершинам, имею-щим временные метки. Таковыми в этот момент являются все вершины, кроме вершины 0. Вы-числяем числа Zдля всех этих вершин. Так как на 0-ой итерации с = 0, P(c) = 0, то имеем (см. граф) P(0)+l(0,1)=1, P(0)+l(0,2)=5, P(0)+l(0,х)=∞ для х=3,4,5. Поэтому в 1-ую строку под знаком Zзаписываются числа 1, 5 и знаки ∞, ∞, ∞. Далее, сравнивая эти значения со значениями Tиз предыдущей строки, записываем под знаком Tв данную строку минимумы, а под знаком Rв тех столбцах, где произошли изменения в T – последнюю помеченную вершину изстолбца с (в данном случае 0). Выбирая минимальное значение из записанных значений T, получаем 1 в столбце для вершины 1. Поэтому записываем 1 (номер вершины) под с и 1 (длина кратчайшего пути) под P.

На 2-ой итерации обрабатываются только столбцы, соответствующие вершинам 2, 3, 4 и 5. Так как на 1-ой итерации с=1, P(c)=1, то имеем (см. граф) P(1)+l(1,2)=9, P(1)+l(1,3)=11, P(1)+ l(1,4)=7, P(1)+l(1,5)=∞. Поэтому во 2-ую строку под знаком Zзаписываются числа 9,11,7 и знак ∞. В клетке справа и сверху от этих чисел записаны (под знаком T) предыдущие временные метки: 5,∞,∞,∞. В клетку во 2-ой строке под знаком T записываем новые временные метки - наименьшие значения из этих двух чисел; получаем 5,11,7 и ∞. Под знаком R в 3-ей и 4-ой группах столбцов во 2-ой строке пишется текущий номер c=1. Выбирая минимальное значение из записанных значений T, получаем 5 в столбце для вершины 2. Поэтому записываем 2 (номер вершины) под с и 5 (длина кратчайшего пути) под P.

На 3-ьей итерации обрабатываются только столбцы, соответствующие вершинам 3,4 и 5. Так как на 2-ой итерации с=2, P(c)=5, то имеем (см. граф) P(2)+l(2,3)=∞, P(2)+l(2,4)=12, P(2)+ l(2,5) = ∞. Поэтому в 3-ью строку под знаком Zзаписываются ∞, 12, ∞. В клетке справа и сверху от этих чисел записаны (под знаком T) предыдущие временные метки: 11, 7,∞. В клетку в 3-ьей строке под знаком T записываем новые временные метки - наименьшие значения из этих пар чисел: 11, 7 и ∞. Под знаком R во всех трёх столбцах ничего не меняется, так как временные метки в них не изменились. Выбирая минимальное значение из записанных значений T, получа-ем 7 в столбце для вершины 4. Поэтому записываем 4 (номер вершины) под с и 7 (длина крат-чайшего пути) под P.

На 4-ой итерации рассматриваются только две вершины: 3 и 5. Новые временные метки для них совпадают. В этом случае можно выбрать любую. Выбираем вершину 3 и в соответст-вии с этим заполняем 4-ую строку и далее – последнюю, 5-ую строку.

Найдём теперь, в соответствии с шагом F АД, сами кратчайшие пути. Просматриваем вершины в том порядке, в каком они идут во 2-ом столбце (в этом порядке они получают посто-янные метки).

Для вершины 1 последнее заполненное значение под знакомRравно 0. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 1 является начальная вершина 0. Поэтому имеем путь 0→1 длины 1.

Для вершины 2 последнее заполненное значение под знакомRравно 0. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 2 является начальная вершина 0. Поэтому имеем путь 0→2 длины 5.

Для вершины 4 последнее заполненное значение под знакомRравно 1. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 4 является вершина 1. Поскольку для вер-шины 1 кратчайший путь таков: 0→1, то имеем путь 0→1→4 длины 7.

Для вершины 3 последнее заполненное значение под знакомRравно 1. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 3 является вершина 1. Поскольку для вер-шины 1 кратчайший путь таков: 0→1, то имеем путь 0→1→3 длины 11.

Для вершины 5 последнее заполненное значение под знакомRравно 4. Это означает, что предпоследней вершиной на кратчайшем пути из 0 в 5 является вершина 4. Поскольку для вер-шины 4 кратчайший путь таков: 0→1→4, то имеем путь 0→1→4→5 длины 11 ■

Пример 2. Рассмотрим применение АД для графа, показанного на рис.1. Длины рёбер на-писаны на рисунке прямо около них. Составим вышеупомянутую таблицу 2. Она содержит все ответы, найденные аналогично примеру 1.

Кратчайшие пути из вершины 0 таковы:

в вершину 1: 0→1;

в вершину 5: 0→5;

в вершину 2: 0→1→2;

в вершину 3: 0→1→3;

в вершину 4: 0→1→4;

в вершину 7: 0→1→2→7;

в вершину 6: 0→5→6.

Длины путей находятся в столбцах «Последний помеченный». Слева стоят номера вершин в порядке получения постоянных меток; справа – длины кратчайших путей в эти вершины.

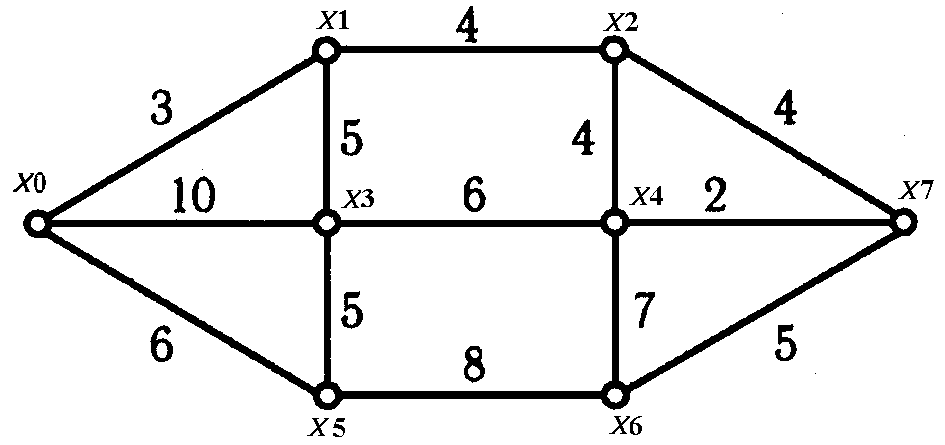
Рис.2

Таблица 2

Итера-ции

Посл помеч

Вершина 0

Вершина 1

Вершина 2

Вершина 3

Вершина 4

Вершина 5

Вершина 6

Вершина 7

№

c

P

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

Z

T

R

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

∞

■

Задание 1. Используя АД, найти кратчайшие пути между вершиной 0 и остальными вершинами в заданных графах. Длины рёбер написаны рядом с рёбрами.

■

Замечание.Рассмотренный алгоритм находит кратчайшие пути в неориентированном графе. Однако этот же самый алгоритм находит кратчайшие ориентированные пути в ориенти-рованном графе (см. все определения в разделе 6-3). Просто в описании алгоритма надо все упоминаемые там рёбра заменить на дуги. В частности, l(c, x) будет означать длину дуги (c, x), ведущей из вершины cв вершину x.

Алгоритм Флойда-Уоршолла

В этом разделе рассматривается другой способ решения задачи о кратчайших путях для всех пар вершин ориентированного графа. В отличие от алгоритма Дейкстры, в АФУ допуска-ются дуги с отрицательной длиной. Однако циклы с отрицательной длиной запрещаются; точн-ее, предполагается, что такие циклы в рассматриваемом графе G = áX,Vñ отсутствуют. Если же циклы отрицательной длины присутствуют, то этот факт выясняется уже в процессе выполнения алгоритма

АФУ основан на представлении пути, ведущего из вершины a в вершину b и проходяще-го через промежуточную вершину c как последовательность двух путей: из a в c и из cв b. По-нятно, что если этот путь является кратчайшим среди всех путей того же вида (т.е. ведущих из a в b через c), то указанные части также должны быть кратчайшими. В алгоритме особую роль играют промежуточные вершины с максимальным номером (в некоторой заданной нумерации вершин).Промежуточнойвершиной простого пути р = áv₁, v₂, ..., v_lñ будем называть любую из вершин v₂, ..., v_l−1.

Будем считать, что вершины графа G = áX,Vñ занумерованы числами от 1 до n. Длина дуги с началом в вершине iи концом в вершинеjобозначена черезl(i,j) (как и в других ситуациях, l(i,j) = 0, еслиi = j,иl(i,j) = ∞, если дуги(i, j)в графе нет). Рассмотрим произвольное k ≤ n. Для данной пары вершинi, jÎV рассмотрим все пути изi в j, у которых все промежуточные вершины принадлежат множеству {1, 2, …, k}. Пусть p − путь минимальной длины среди всех таких путей. Он является простым путём, поскольку предполагается, что в графе нет циклов отрицательной длины. Как найти длину этого пути, зная длины всех таких (кратчайших) путей для всех пар вершин при мéньших k?

Для пути p есть две возможности.

Если k не входит в р, все промежуточные вершины пути p содержатся в множестве {1, 2, …, k−1}. Тогда путь р является кратчайшим путём из i в j, промежуточные вершины которого принадлежат множеству{1, 2, …, k−1}.

Если k является промежуточной вершиной пути р, она разбивает его на два участка р₁ и р₂ (вершина k встречается лишь однажды, гак как р− простой путь). Поэтому путьр₁ будет кратчайшим путём изi в k,путь р₂будет кратчайшим путём из k в j,а промежуточными вершинами на обоих путях будут вершины из множества {1, 2, …, k−1}. Эти рассуждения лежат в основе излагаемого ниже алгоритма.

Алгоритм Флойда-Уоршолла (АФУ). Алгоритм находит кратчайшие пути для всех пар вершин заданного ориентированного графаG. Для реализации алгоритма вводятся четыре квадратные матрицы размера n´n, где n – число вершин в заданном графе G:

Матрица D = (d_ij) текущих кратчайших расстояний;

Вспомогательная матрица H = (h_ij) для пересчёта текущих кратчайших расстояний;

Матрица предшествия Π= (π_ij) (матрица предпоследних вершин на текущих кратчайших путях из i в j);

Вспомогательная матрица Ψ = (ψ_ij) для пересчёта предпоследних вершин.

В процессе работы алгоритма происходит заполнение матриц и изменение их элементов. Алго-ритм прекращает работу после n-го шага.

Шаг 0 (Инициализация). Положить

d_ij = l(i, j) (i, j = 1, …, n);

π_ij= .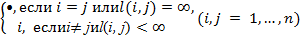

Шагk(1≤k ≤n).

1. Для всех i, j= 1, …,nвыполнить следующие операции:

1.1. Положить

z = d_ik + d_kj, (2)

1.2. Если z<d_ij, то положить h_ij = z и ψ_ij = π_kj. В противном случае положить h_ij = d_ij и ψ_ij = π_ij. Заметим, что из d_ik = ∞ следует, что z = ∞ и неравенство z<d_ij не выполняется.

2. Для всех i, j= 1, …,nположить d_ij = h_ij, π_ij= ψ_ij.

ШагF.На этом шаге определяются кратчайшие пути для всех пар вершин. Кратчайший путь из начальной вершины i в любую другую вершину j строится следующим образом: верши-ной, предшествующей jна искомом пути, является вершина p = π_ij; вершиной, предшест-вующей pна искомом пути, является вершина q = π_ip, и т.д., вплоть до начальной вершины i. Искомый путь из i в jсостоит из тех же вершин в обратном порядке ■

При «ручной» реализации АФУ будет удобно результаты каждой итерации записывать в последовательные таблицы специального вида – по одной на каждую итерацию. Реализация АФУ состоит в последовательном заполнении таблиц и переносе части результатов в следую-щую таблицу. Эта схема подробно описана при нахождении всех кратчайших путей в конкрет-ном графе, рассмотренном в следующем примере.

Пример 3. Проиллюстрируем работу АФУ на примере графа, показанного на рис.3. На этом рисунке рядом с вершинами показаны их номера; более крупным шрифтом рядом с дуга-ми показаны их длины.

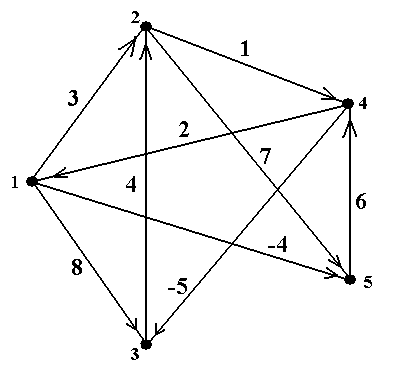
Рис. 3. Ориентированный граф с 5-ью вершинами и 9-ью дугами

Все операции алгоритма являются операциями над данными, записанными в таблицу типа таблицы 3. В эту таблицу входит 5×5 ячеек, каждая из которых состоит из трёх клеток. Эти клетки будут называться левой, средней и правой. Кроме этих 25 ячеек, таблица содержит ле-вый столбец, состоящий из 5-и клеток, и верхнюю строку, состоящую из 5 ячеек, содержащих по 2 клетки каждая (левую и правую). Их роль будет указана ниже.

Таблица 3. Исходная таблица для АФУ

№

Инициализация. Она состоит в заполнении таблицы 4.1а, совпадающей с таблицей 3. По-следовательно рассматриваются все дуги исходного графа, показанного на рис.3. Если дуга ве-дёт из вершины i в вершину j, то в среднюю клетку ячейки с индексом (i, j) (т.е. находящуюся на пересечении i-ой строки и j-го столбца) вставляется длина дуги из вершины i в вершину j, а в правую клетку – номер i. После этого во всех ячейках с совпадающими индексами (i, i) в среднюю клетку записывается 0. Наконец, во всех остальных ячейках в средние клетки напи-шем знак ∞. Больше ничего в таблицу 4.1а не записывается. Все упомянутые данные берутся непосредственно из рис.3. В дальнейших конструкциях рисунок не участвует.

Таблица 4. Результат инициализации

№

∞

−4

∞

∞

∞

∞

∞

∞

−5

∞

∞

∞

∞

Итерация 1.k = 1. На итерации 1 происходит последовательное преобразование данных, полученных при инициализации и представленных в таблице 4. Сначала заполняются левый столбец и верхняя строка. В i-ую клетку левого столбца копируется содержимое из средней клетки ячейки с индексом (i, k) (номер kравен номеру итерации, и в данном случае k = 1). В j-ую ячейку верхней строки копируется содержимое средней и правой клеток ячейки с индексом (k, j) (k = 1). Результат этой операции приведён в таблице 4.1a. Заметим, что при копировании пустой клетки её копия также будет пустой клеткой.