Анализ напряженно-деформированного состояния в точке тела
Раздел 12
I. Объемное напряженное состояние
1. Полное, нормальное и касательное напряжения на наклонной площадке
На рис. 11.3 показаны компоненты полного напряжения 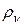 на наклонной площадке
на наклонной площадке 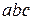 . Очевидно, что его численное значение определяется так
. Очевидно, что его численное значение определяется так
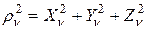
Подставляя сюда формулы (11.4) найдем
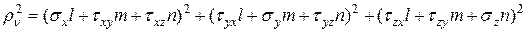 (12.1)
(12.1)
Здесь 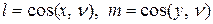 и
и 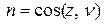 – направляющие конусы нормали
– направляющие конусы нормали 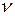 к площадке
к площадке 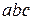 . Полное напряжение
. Полное напряжение 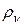 можно разложить на
можно разложить на 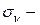 нормальное и
нормальное и 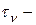 касательное напряжения на наклонной площадке. Очевидно, что
касательное напряжения на наклонной площадке. Очевидно, что 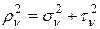 . Напряжение
. Напряжение 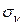 можно найти, проектируя
можно найти, проектируя 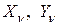 и
и 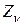 на нормаль
на нормаль 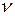 , т.е.
, т.е. 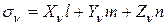 . С учетом формул (11.4) получим
. С учетом формул (11.4) получим
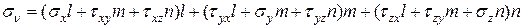 (12.2)
(12.2)
Касательное напряжение 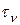 можно найти так
можно найти так
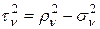 (12.3)
(12.3)
2. Главные напряжения, главные площадки
На наклонной площадке, у которой орт нормали 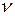 совпадает с направлением
совпадает с направлением 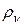 , величина
, величина 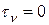 , а
, а 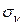 будет экстремально и равно
будет экстремально и равно 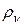 . Такая площадка называется главной (ее направление определяют направляющие косинусы, которые обозначим
. Такая площадка называется главной (ее направление определяют направляющие косинусы, которые обозначим 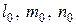 ). А напряжения на ней обозначим
). А напряжения на ней обозначим 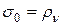 . Все его проекции на оси
. Все его проекции на оси 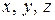 будут
будут 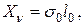
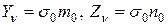 . Подставим их в формулы (11.4)
. Подставим их в формулы (11.4)
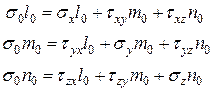 или
или 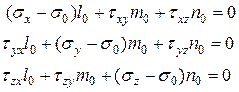 (1)
(1)
Надо найти 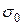 и
и 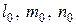 при известных напряжениях в точке тела
при известных напряжениях в точке тела 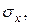
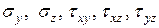 .
.
Очевидно, что 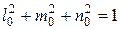 .
.
Из этого следует, что 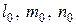 одновременно не могут быть равны нулю. Тогда система уравнений (1) имеет решение, если ее определитель
одновременно не могут быть равны нулю. Тогда система уравнений (1) имеет решение, если ее определитель 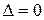 , т.е.
, т.е.
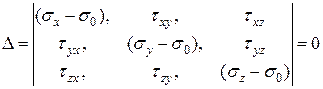 (3)
(3)
Раскрывая этот определитель получим, с учетом закона парности касательных напряжений:
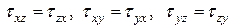 (4)
(4)
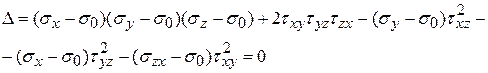 (5)
(5)
После перемножений и приведения подобных членов найдем
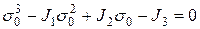 (12.4)
(12.4)
Где: 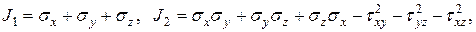
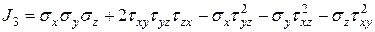 (12.5)
(12.5)
Величины 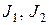 и
и 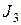 называются инвариантами тензора напряжений
называются инвариантами тензора напряжений 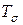 (легко убедится, что
(легко убедится, что 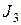 есть определитель
есть определитель 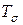 ). При повороте осей
). При повороте осей 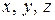 компоненты
компоненты 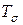 меняются, но
меняются, но 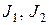 и
и 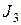 при этом не должны меняться, т.к.
при этом не должны меняться, т.к. 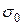 , определяемые из (12.4), не зависят от выбора положения осей
, определяемые из (12.4), не зависят от выбора положения осей 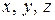 , а зависят от нагружения тела.
, а зависят от нагружения тела.
Решение кубического уравнения (12.4) дает три корня для 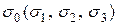 , которые и называются главными напряжениями. Итак, имеем три главных напряжения, которые действуют на трех главных площадках, определяемых
, которые и называются главными напряжениями. Итак, имеем три главных напряжения, которые действуют на трех главных площадках, определяемых 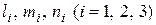 . Например, найдем
. Например, найдем 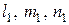 главной площадки, где действует
главной площадки, где действует 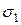 . Для этого составим три уравнения:
. Для этого составим три уравнения: 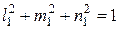 и любых два уравнения из системы (1), подставляя в них
и любых два уравнения из системы (1), подставляя в них 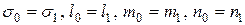 . Решая эти три уравнения, найдем
. Решая эти три уравнения, найдем 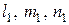 . Аналогично определяются две другие площадки, где действуют
. Аналогично определяются две другие площадки, где действуют 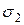 и
и 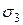 . Можно показать, что главные площадки взаимно ортогональны.
. Можно показать, что главные площадки взаимно ортогональны.
Инварианты напряженного состояния через главные напряжения определяются с учетом (12.5) так:
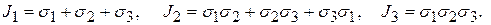
Здесь учтено, что на главных площадках нет касательных напряжений.
3. Экстремальные касательные напряжения
Вырежем из тела малый тетраэдр, у которого координатные оси совпадают с направлениями главных напряжений, т.е. на невидимых площадках действуют только 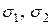 и
и 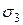 (см. рис. 11.3). Найдем касательное напряжение
(см. рис. 11.3). Найдем касательное напряжение 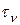 на наклонной площадке с ортом
на наклонной площадке с ортом 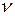 .
.
Полное напряжение на ней 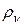 и нормальное
и нормальное 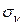 получим из зависимостей (12.1) и (12.2), полагая в них:
получим из зависимостей (12.1) и (12.2), полагая в них: 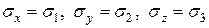 ,
, 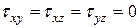 , т.к. на главных площадках касательных напряжений нет
, т.к. на главных площадках касательных напряжений нет
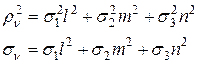 (6)
(6)
Касательные напряжения на наклонной площадке найдем по (12.3), подстановкой (6)
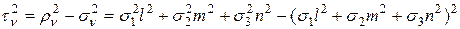
После преобразований, получим
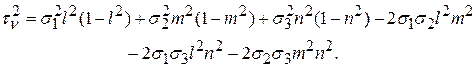 (7)
(7)
Условие экстремальности 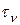 по параметрам
по параметрам 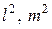 и
и 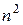 дает три решения, которые определяют три площадки с экстремальными
дает три решения, которые определяют три площадки с экстремальными 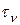 :
:
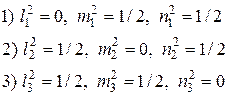 Третьему решению соответствуют рис.а, т.е. это площадка под углами 45° к осям с Третьему решению соответствуют рис.а, т.е. это площадка под углами 45° к осям с 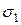 и и 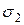 и проходящая через ось 3. Подставляя и проходящая через ось 3. Подставляя 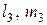 и и 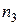 в выражение (7), получим в выражение (7), получим | 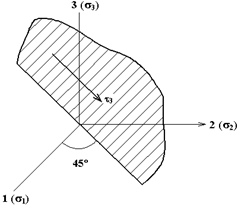 Рис.а Рис.а |
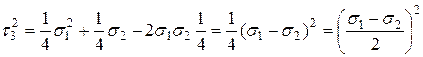
Окончательно
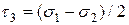 (8)
(8)
Аналогично, на площадках с решениями 1) и 2), можно найти экстремальные 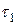 и
и 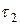 .
.
Итак, имеем три площадки, на которых действуют экстремальные касательные напряжения:
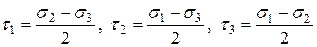 (12.6)
(12.6)
4. Октаэдрические нормальные и касательные напряжения
Площадки, равнонаклоненные к направлениям главных напряжений, называются октаэдрическими, направляющие косинусы их 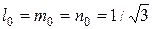 , т.к. должно быть
, т.к. должно быть 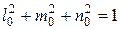 .
.
Нормальное напряжение 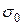 и касательное
и касательное 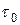 на этой площадке через главные напряжения найдем по формулам (6) и (7) подстановкой
на этой площадке через главные напряжения найдем по формулам (6) и (7) подстановкой 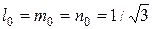
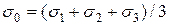
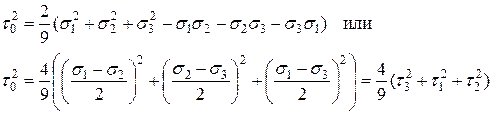 (12.7)
(12.7)
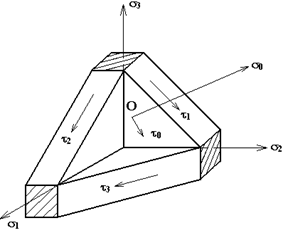 Рис.в Рис.в | Величину 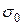 называют часто гидростатическим давлением. С т.О на рис. В обозначена октаэдрическая площадка с называют часто гидростатическим давлением. С т.О на рис. В обозначена октаэдрическая площадка с 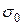 и и 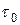 , заштрихованы главные площадки с , заштрихованы главные площадки с 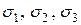 и показаны три площадки с экстремальными касательными напряжениями и показаны три площадки с экстремальными касательными напряжениями 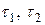 и и 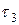 . Легко показать, что . Легко показать, что 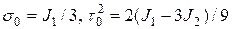 , следовательно, , следовательно, 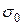 и и 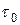 тоже тоже |
являются инвариантами по отношению к преобразованию координатных осей.
II. Плоское напряженное состояние
а) Полное, нормальное и касательное напряжения на наклонных площадках
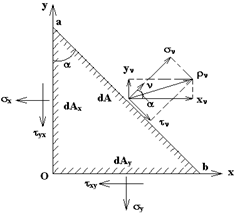 |
Рис. 12.1
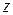 , т.е.
, т.е. 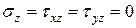 (9) Получим ПНС в осях
(9) Получим ПНС в осях 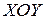 , показанное на рис. 12.1.
, показанное на рис. 12.1. На наклонной площадке 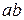 действует полное напряжение
действует полное напряжение 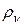 , которое можно разложить:
, которое можно разложить:
1. на составляющие по осям 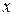 и
и 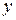 , т.е. на
, т.е. на 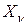 и
и 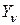 ;
;
2. на нормальное 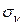 и касательное
и касательное 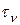 напряжения.
напряжения.
Очевидно: 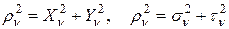 (10)
(10)
Как и в объемном напряженном состоянии, положение площадки 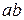 определим так (см. рис. 12.1):
определим так (см. рис. 12.1):
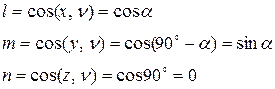 (11)
(11)
Напряжения 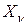 и
и 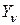 здесь определяются из уравнений (11.4), подставляя в них (9) и
здесь определяются из уравнений (11.4), подставляя в них (9) и 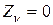
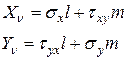 (12.7)
(12.7)
Здесь 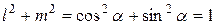 .
.
Уравнения (12.7) легко получить из условий равновесия треугольного элемента, показанного на рис.12.1 Определим площадки элемента:
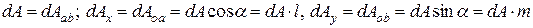 (13)
(13)
Умножая напряжения на площадки, составим уравнения статики
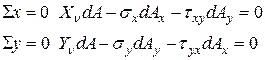
Подставляя (13) и сокращая на 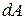 , получим формулы (12.7). Нормальное напряжение
, получим формулы (12.7). Нормальное напряжение 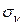 найдем, проектируя
найдем, проектируя 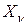 и
и 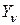 на нормаль
на нормаль 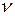 к площадке
к площадке 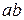 (см.рис. 12.1)
(см.рис. 12.1)
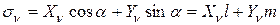
Подставляем (12.7), получим:
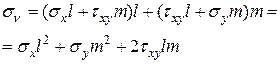
Подставляя (11) и учитывая, что 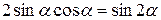 , найдем
, найдем
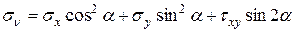 (12.8)
(12.8)
Касательное напряжение 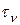 определим, проектируя
определим, проектируя 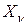 и
и 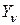 на направление
на направление 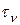 (см. рис. 12.1)
(см. рис. 12.1)
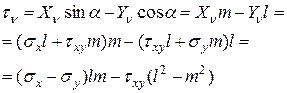
Подставим (11) и учитывая, что 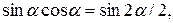
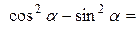
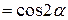 , окончательно получим
, окончательно получим
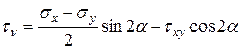 (12.9)
(12.9)
в) Главные напряжения, главные площадки
Здесь, как и в объемном напряженном состоянии, имеются главные площадки с направляющими косинусами 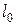 и
и 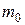 , на которых нормальные напряжения экстремальны и они называются главными напряжениями
, на которых нормальные напряжения экстремальны и они называются главными напряжениями 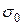 , а касательные напряжения отсутствуют. Поэтому здесь
, а касательные напряжения отсутствуют. Поэтому здесь 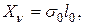
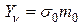 . Подставляя это в формулы (12.7) получим
. Подставляя это в формулы (12.7) получим
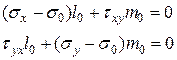 (14)
(14)
Известно, что 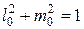 , поэтому уравнения (14) имеют решение, если его определитель
, поэтому уравнения (14) имеют решение, если его определитель 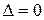
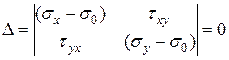
Раскроем этот определитель
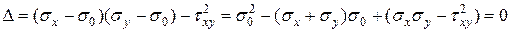 (15)
(15)
Здесь 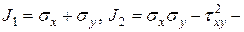 инварианты ПНС.
инварианты ПНС.
Решение квадратного уравнения (15) дает два корня 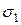 и
и 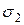 , которые и называют главными напряжениями в ПНС:
, которые и называют главными напряжениями в ПНС:
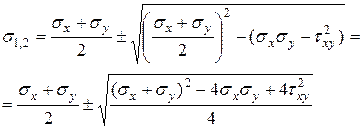
Окончательно получим для 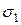 (знак (+)) и
(знак (+)) и 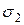 (знак (–)):
(знак (–)):
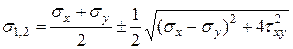 (12.10)
(12.10)
Положение главных площадок, где действуют 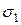 и
и 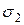 в ПНС удобно определять углами
в ПНС удобно определять углами 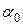 , которые нормали к главным площадкам составляют с осью
, которые нормали к главным площадкам составляют с осью 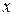 . Их легко определить из условия отсутствия на главных площадках касательных напряжений. Подставляя
. Их легко определить из условия отсутствия на главных площадках касательных напряжений. Подставляя 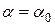 и
и 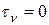 в (12.9) получим
в (12.9) получим
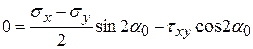
откуда
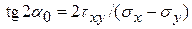 (12.11)
(12.11)
Из (12.11) получим два значения 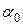 , одно
, одно 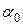 , другое
, другое 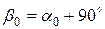 , которые определяют две взаимно ортогональные главные площадки.
, которые определяют две взаимно ортогональные главные площадки. 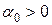 и
и 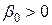 откладывать от оси
откладывать от оси 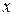 против хода часовой стрелки.
против хода часовой стрелки.
Чтобы не выяснять, на каких площадках действуют 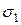 и
и 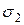 , надо подставить
, надо подставить 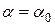 и
и 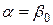 в формулу (12.8), большая величина
в формулу (12.8), большая величина 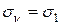 , а меньшая
, а меньшая 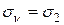 . Эти величины
. Эти величины 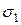 и
и 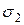 должно быть равны величинам, вычисленным по (12.10).
должно быть равны величинам, вычисленным по (12.10).
с) Экстремальные касательные напряжения
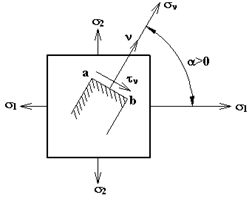 Рис.с Рис.с | Вырежем из тела, испытывающего ПНС, прямоугольный элемент с главными площадками, на которых действуют 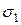 и и 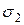 . Выделим наклонную площадку ab, нормаль . Выделим наклонную площадку ab, нормаль 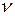 к которой с направлением к которой с направлением 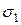 составляет угол составляет угол 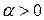 . Напряжения . Напряжения 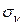 и и 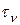 на этой площадке найдем по зависимостям (12.8) и (12.9), полагая на этой площадке найдем по зависимостям (12.8) и (12.9), полагая 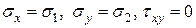 . . |
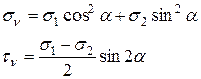 (16)
(16)
Из второй формулы (16) видно, что при 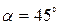
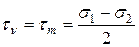 (12.12)
(12.12)
Подставляя сюда 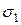 и
и 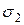 из формулы (12.10), получим
из формулы (12.10), получим
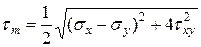 (12.13)
(12.13)
Итак, экстремальные касательные напряжения действуют на площадках под углом 45° к главным и определяются по формулам (12.12) или (12.13).
Нормальные напряжения 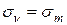 на этих площадках найдем по первой формуле (16), подставляя
на этих площадках найдем по первой формуле (16), подставляя 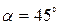 (
( 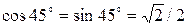 )
)
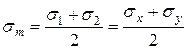 (17)
(17)
Здесь учтено, что 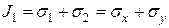 .
.
d) Чистый сдвиг
Рассмотрим частный случай ПНС, когда главные напряжения 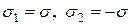 .
.
В этом случае экстремальные 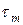 найдем по (12.12), а нормальные напряжения
найдем по (12.12), а нормальные напряжения 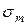 на этих площадках по (17). Итак
на этих площадках по (17). Итак
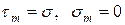
Такой случай носит название чистый сдвиг.
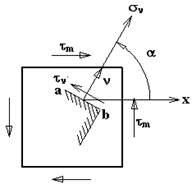 Рис. d Рис. d | Вырежем из тела прямоугольный элемент, испытывающий чистый сдвиг, т.е. по его граням действуют только 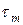 . Найдем нормальное напряжение . Найдем нормальное напряжение 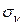 и касательное и касательное 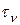 на наклонной площадке на наклонной площадке 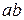 под углом под углом 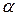 (рис. d). Используя формулы (12.8) и (12.9), подставляя в них: (рис. d). Используя формулы (12.8) и (12.9), подставляя в них: 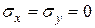 , , 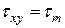 . Получим . Получим 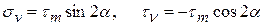 (12.14) (12.14) |
Из этих формул видно, что при 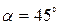
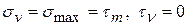 , а это как известно, характеристики главной площадки.
, а это как известно, характеристики главной площадки.
Итак, при чистом сдвиге главные площадки расположены под углом 45° к площадкам чистого сдвига, а главные напряжения на них:
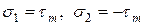 (при
(при 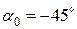 )
)
III. Анализ деформированного состояния
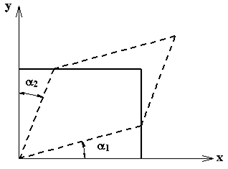 | 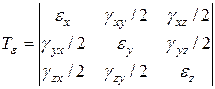 Тензор деформации Тензор деформации 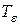 представим в симметричном виде (см. рис), когда представим в симметричном виде (см. рис), когда 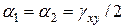 и т.д. Анализ деформиро-ванного состояния проведем по аналогии с и т.д. Анализ деформиро-ванного состояния проведем по аналогии с |
вышеприведенным анализом напряженного состояния. Три взаимно ортогональных направления, сдвиги между которыми при деформации тела равны нулю, называются главными деформациями и обозначаются 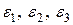 .
.
Главные деформации находятся из уравнения, аналогичного уравнению (12.4) для определения главных напряжений
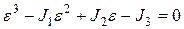 (12.15)
(12.15)
Здесь 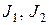 и
и 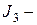 инварианты деформированного состояния:
инварианты деформированного состояния:
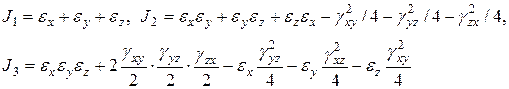 (12.16)
(12.16)
Решение кубического уравнения (12.15) дает три величины главных деформаций 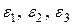 .
.
В случае плоской деформации, когда, например, 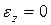 по аналогии с ПНС, формулы (12.10), получим
по аналогии с ПНС, формулы (12.10), получим 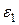 и
и 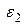
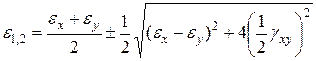 (12.17)
(12.17)
Экстремальные сдвиги находятся по формулам, аналогичным (12.6) для определения экстремальных касательных напряжений
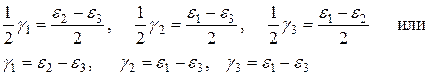 (12.18)
(12.18)
Для изотропных материалов направления главных деформаций совпадает с направлениями главных напряжений.
Выясним физический смысл инварианта 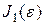 : Рассмотрим кубик, у которого ребра совпадают с направлениями главных деформаций и до нагружения тела их длины равны 1. Его объем
: Рассмотрим кубик, у которого ребра совпадают с направлениями главных деформаций и до нагружения тела их длины равны 1. Его объем 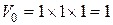 . После деформации его объем станет
. После деформации его объем станет 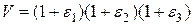 . Относительное изменение объема обозначим
. Относительное изменение объема обозначим 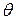
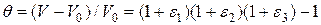
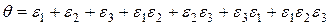
Деформации 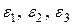 малы, поэтому величины второго и третьего порядка малости можно не учитывать, тогда
малы, поэтому величины второго и третьего порядка малости можно не учитывать, тогда
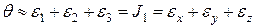 (12.19)
(12.19)
Итак, первый инвариант деформированного состояния определяет относительное изменение объема тела.
Октоэдрический сдвиг, по аналогии с (12.7) – октаэдрических касательных напряжений, определяется так
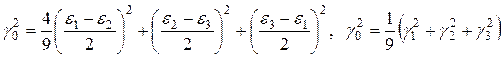 (12.20)
(12.20)
Последняя формула получена с учетом (12.18)
